电液伺服闭式泵控系统位置前馈补偿控制研究

2019-12-12陈革新1赵鹏辉1刘小胜4闫桂山1超23

液压与气动 2019年12期

陈革新1，赵鹏辉1，刘小胜4，闫桂山1，艾超23

(1.燕山大学机械工程学院，河北秦皇岛 066004; 2.河北省重型机械流体动力传输与控制实验室，河北秦皇岛 066004;3.先进锻压成型技术与科学教育部重点实验室(燕山大学)，河北秦皇岛 066004；4.格特拉克(江西)传动系统有限公司，江西南昌 330013)

引言

电液伺服技术在冶金、锻压、军工、船舶、轨道交通等工业领域均有极其重要的应用，是工业制造装备领域的核心技术之一。其中，电液伺服闭式泵控系统便是其中一个重要的方向[1]，该系统由伺服电机、定量泵、蓄能器、液压缸和控制器等组成，能有效解决电液伺服阀控技术存在的固有缺陷，如抗污染能力差、集成度低、能源浪费严重、设备装机成本高以及维护不便等问题；相较于电液伺服阀控设备，该系统具有设备体积小、管路布置简单、无节流溢流损失等特点[1]。

位置控制技术是电液伺服闭式泵控系统的重要研究方向，国内外专家学者采用自适应控制[3-5]、滑模变结构控制[6]、模糊控制等[7-8]技术对电液伺服系统位置控制进行了相关研究，并针对闭式泵控系统位置控制中负载扰动和参数不确定性问题，进行了粒子群优化的模糊逻辑控制器设计[9-10]、鲁棒模型预测控制器设计[11]、离散滑模控制算法处理[12]等相关研究。上述研究为电液伺服闭式泵控系统位置控制研究奠定了良好的基础。

本研究针对电液伺服闭式泵控系统位置控制问题，提出前馈补偿控制方法，进而提高系统动态响应，减小系统位置控制误差，最终进行实验研究验证。

1 电液伺服闭式泵控系统平台

1.1 电液伺服闭式泵控系统

电液伺服闭式泵控系统原理图，如图1所示。

图1 电液伺服闭式泵控系统原理图

该系统由伺服电机同轴驱动定量泵，定量泵吸排油口直接连接液压缸两负载油口；通过控制伺服电机的转速与转矩，调节电液执行器的位移、速度等。

1.2 数学模型建立

1) 定量泵的流量方程

定量泵的转速为：

ωp=Kpu

(1)

式中，Kp—— 伺服电机转速梯度，rad/(s·V-1)

u—— 伺服电机指令电压信号，V

ωp—— 定量泵角速度，rad/s

定量泵的流量连续性方程为：

qp=Dpωp-CtppL

(2)

式中，Dp—— 定量泵排量，m3/rad

qp—— 定量泵流量，m3

pL—— 系统压力，MPa

Ctp—— 定量泵总泄漏系数，m3/(s·Pa)

2) 液压缸的流量连续性方程

(3)

式中，Ap—— 液压缸有效作用面积，m2

Ctc—— 液压缸总泄漏系数，m3/(s·Pa)

Vt—— 总压缩容积，m3

βe—— 有效体积弹性模量，Pa

3) 液压缸和负载的力平衡方程

(4)

式中,mt—— 活塞上的总质量，kg

Bp—— 总黏性阻尼系数，N/(m·s-1)

K—— 负载弹簧刚度，N/m

FL—— 活塞上的任意外负载力，N

式(1)～式(3)是泵控缸的3个基本方程，描述了泵控缸的动态特性。三式的拉氏变换式为：

QL=DpKpu-CtppL

(5)

(6)

AppL=mts2Xp+BpsXp+KXp+FL

(7)

由式(5)～式(7)可得出泵控对称液压缸的位置传递函数如下:

(8)

式中,Ctc—— 液压缸总泄漏系数,m3/(s·Pa)

ζh—— 液压系统阻尼比

ωh—— 液压系统固有频率，rad/s

1.3 前馈补偿控制器设计

由电液伺服闭式泵控系统位置控制分析可知，影响系统控制精度和响应速度的关键问题在于系统的参数不确定性和外负载的随机扰动，本研究针对该问题提出了一种基于期望轨迹规划，如图2期望轨迹规划曲线(根据实际运动状态、运动速度和运动方向，将计算所请求运动的特征角点，可将该运动划分为三个阶段，加速阶段、匀速阶段、减速阶段)的前馈补偿控制方法。

图2 期望轨迹规划曲线

前馈补偿控制方法以期望轨迹规划的速度作为中间控制变量，依据负载扰动引起的系统流量的变化实时补偿定量泵的转速，确保系统高精度输出。由式(1)～式(4)可得，前馈补偿数学模型为：

(9)

式中，ωm—— 伺服电机转速补偿，rad/s

Vref—— 期望转速，rad/s

闭式泵控对称缸系统在位置控制的过程中，采用前馈补偿控制方法，配合位置偏差闭环控制，其控制原理图如图3所示。

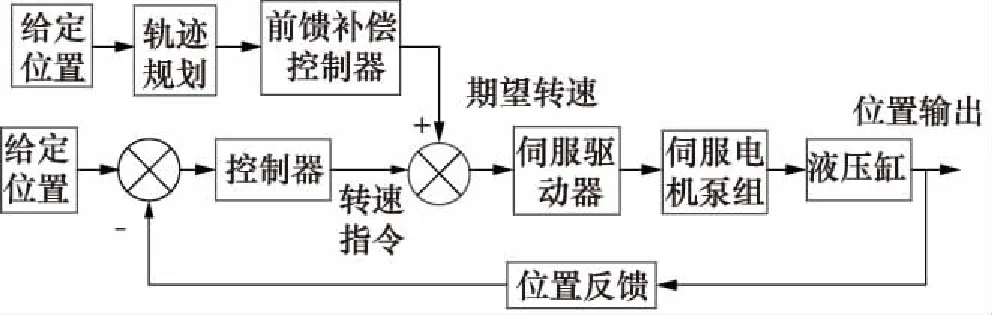
图3 位置前馈补偿控制原理图

以上述前馈补偿控制数学模型为基础，结合式(1)～式(4)和图3分析可得，系统位置前馈补偿控制传递函数框图如图4所示。

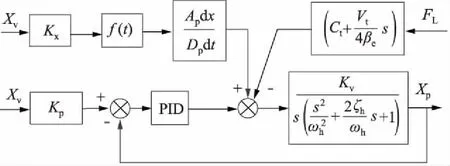
图4 位置前馈补偿控制传递函数控制框图

由图4分析可知，闭式泵控对称缸位置控制包括两部分，第一部分是位置闭环控制系统，第二部分是前馈补偿。位置闭环控制系统采用经典PID控制，对系统的位置调节进行基本的控制，引入前馈补偿控制部分，该部分控制器的控制原则是，依据目标位移规划系统期望速度，求解伺服电机转速补偿基准值，直接输出控制信号满足实际运动曲线的速度要求，最终使得系统响应速度更快，控制精度更高，到达稳态误差所用时间短。

2 电液伺服闭式泵控实验平台

基于上述电液伺服闭式泵控位置控制系统，搭建试验平台如图5所示：试验台主要有驱动器、控制器、上位机、电液伺服动力单元(定量泵和伺服电机)、阀台(包括各类阀件、传感器、蓄能器、过滤器以及测压装置)、液压缸等组成。试验台部分参数如表1所示。

1.驱动器 2.阀台 3.控制器 4.电液伺服动力单元 5.位移传感器 6.执行机构图5 电液伺服闭式泵控系统位置控制试验台

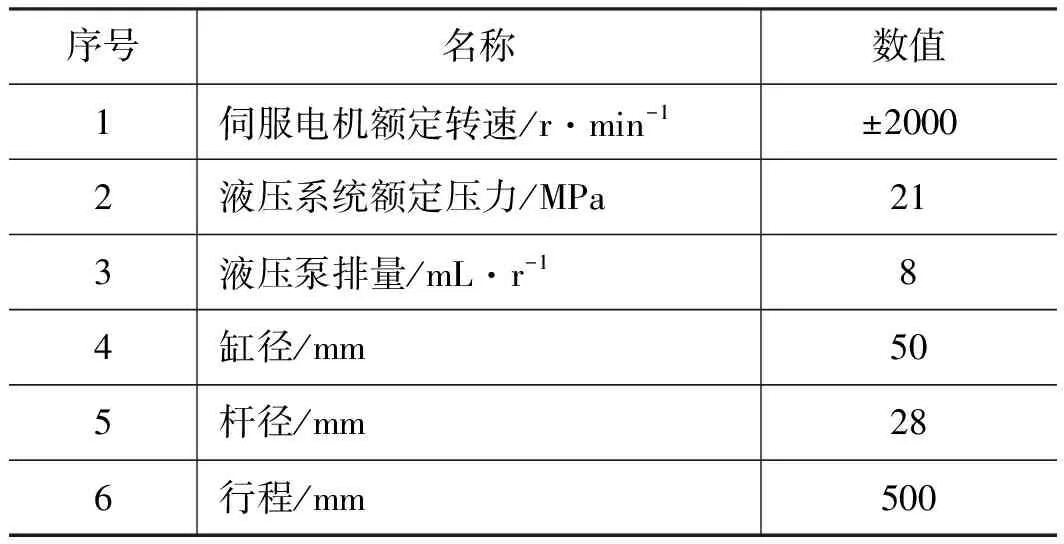
表1 电液伺服闭式泵控系统参数

3 试验结果分析

首先进行经典的PID控制算法调试，经典的PID控制器具体参数如表2所示，然后加入前馈补偿控制观察位置曲线变化，两者作为对比。试验分别进行了100，200 mm距离的2种控制器位置闭环控制试验。

表2 经典PID控制参数与实验结果

3.1 经典PID控制

首先进行经典电液伺服PID位置控制试验，试验曲线如图6和图7所示。

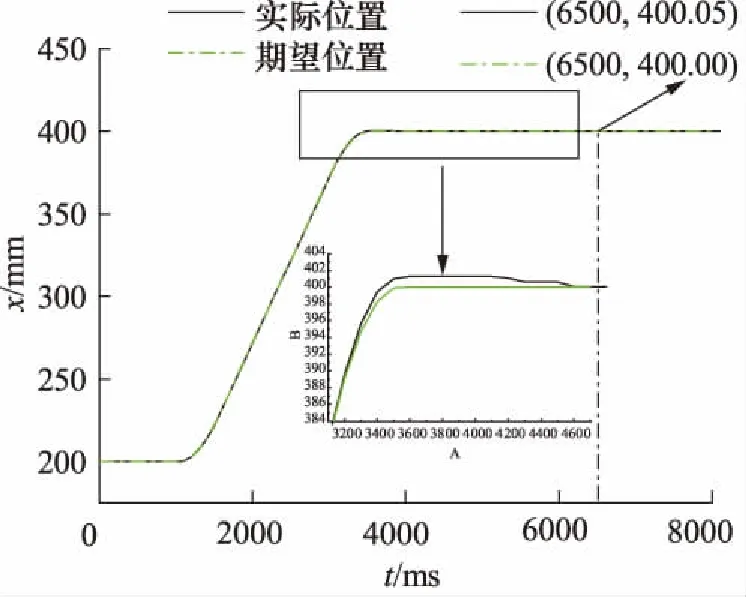
图6 经典PID控制的油缸位置伸出变化曲线

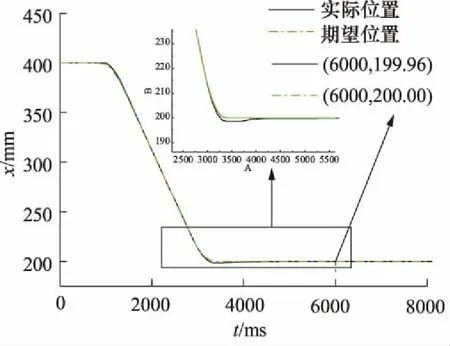
图7 经典PID控制的油缸位置缩回变化曲线

由经典PID位置控制实验变化曲线分析可得出，在液压缸匀速伸出和缩回阶段，液压缸的实际位置与目标位置变化贴合，但是在加减速阶段存在较大偏差，出现超调现象，且油缸前进过程最后稳定误差为0.05 mm,而且最终稳定时间大约需要6.5 s，稳定时间较长；油缸缩回过程最后稳态误差为0.04 mm，而且稳定时间较长大约为6 s左右。

3.2 位置前馈补偿控制调节

基于目标位置轨迹规划，预设目标运动曲线，计算预期位置、速度与加速度，由于外负载扰动引起的流量稳定性，进行定量泵转速补偿，消除稳态波动。加入前馈补偿控制环节，进行试验，试验曲线如图8和图9所示。

图8 加入前馈补偿环节的油缸位置伸出变化曲线

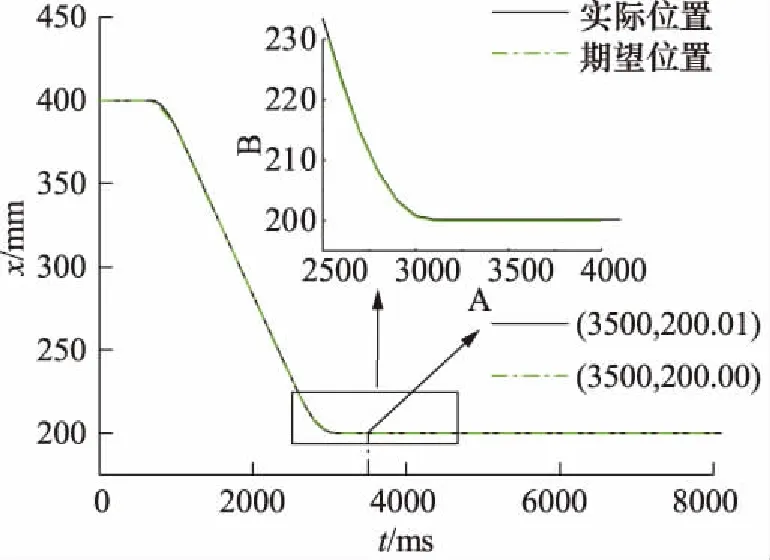
图9 加入前馈补偿环节的油缸位置缩回变化曲线

由加入位置前馈补偿环节的液压缸位置变化曲线可以分析出，实际位置曲线与目标位置曲线基本保持一致，此时系统全程已经处于最佳状态。油缸伸出阶段稳态误差为0.02 mm，没有超调现象，达到最终稳态所需时间3.5 s左右，相较经典PID控制稳态误差缩小0.03 mm，稳定时间缩短3 s；在油缸缩回阶段稳态误差为0.01 mm，达到最终稳态所需时时间3.5 s左右，相较经典PID控制稳态误差缩小0.03 mm，达到最终稳态所需时间缩短2.5 s。