江苏及邻区地方性震级量规函数的研究

康清清 顾勤平 于悦颖 钱婷 黄群 霍祝青

1)江苏省地震局,南京 210014

2)中国地震局地球物理研究所,北京 100081

3)江苏省无锡地震台,江苏无锡 214000

4)江苏省溧阳地震台,江苏溧阳 213300

0 引言

震级是表征地震大小的物理量,许多研究工作如地震统计、震源物理研究、地震烈度、地震与前兆现象的关系等都与其密切相关(陈培善等,1983),提供统一、准确的震级标度,无论是从地震预测科学还是社会应对策略角度均是一件有意义的重大基础性工作(刘瑞丰等,2017)。我国省级测震台网量取的震级类型主要是地方性震级ML,影响该震级类型计算的因素主要有量规函数、台基效应、地震震源(地震辐射方向)等(严尊国,1986)。其中量规函数描述了地震波随距离衰减的特性,与地壳构造紧密相关,具有明显的区域特征(薛志照,1992),不同地区的地震波衰减特性各不相同。因此,建立与本地区的地壳特征相对应的量规函数十分必要。

我国地震工作者围绕量规函数开展了大量的研究,李善邦(1981)结合我国当时常用的短周期地震仪器和基式中长周期地震仪器的特性,得到了量规函数R1(Δ)和R2(Δ),在全国范围内推广使用。严尊国等(1992、1995)依据我国广大地区的实际观测资料,分别确定了我国东部和西部地区的地方性震级量规函数,并约定了其使用区域。刘瑞丰等(2015、2017、2018)对2002年以前全国各测震台网的大量观测资料进行震级方面的深入研究,形成了新震级国家标准GB17740-2017(以下简称“新国标”),建立了我国分区地方性震级量规函数(王丽艳等,2016)。

针对全国性的量规函数,在特定区域范围内对观测资料展开研究,可以进一步修正和完善原量规函数,使之更趋于合理化。多个省级区域测震台网根据属地化原则,针对所管辖区域开展了更为细致的工作,如河北、福建、山西、江西、甘肃、广东、新疆等地的台网已分别取得了适用于本地区的有益结果(赵明淳等,2005；林仙坎,2006；孟晓琴等,2008；项月文等,2010；陈继锋等,2013；吕作勇等,2015；张志斌等,2018),而江苏省地震局测震台网自数字化以来还未进行过相关研究。

自2009年以来,江苏及相邻数字测震台网已积累了大量宽频带数字地震观测资料,为建立该区域量规函数提供了契机。本文借鉴前人所做的工作,在新国标量规函数的基础上进行校正,试图得到更适用于江苏及邻区的地方性震级量规函数,以提高江苏省地震台网地方性震级测定的精度。

1 台网概况和资料选取

“十五”数字化改造以来,江苏省数字地震台站已覆盖全省,目前共有75个数字测震台站,其中,深井台站31个,地面台站44个,平均台间距约为40km。对于苏中沿海地区松散沉积覆盖层,均采用深井观测。为了提高对网缘地震的监控能力,从中国地震台网中心接收河南、山东、安徽、浙江和上海等省(市)34个台站的实时波形数据。本文采用以上台站选出的2009年1月～2018年1月江苏及邻省ML≥1.5、且基本保证有5个以上台站记录的观测资料,经过综合分析、处理、复核后,最终筛选出观测资料良好、且单台震级样本数超过50个的72个台站记录的2602个地震事件。最终选取的台站和地震震中分布见图1 ,共计算得到单台震级数据20173个,震中距范围0.4～500km。

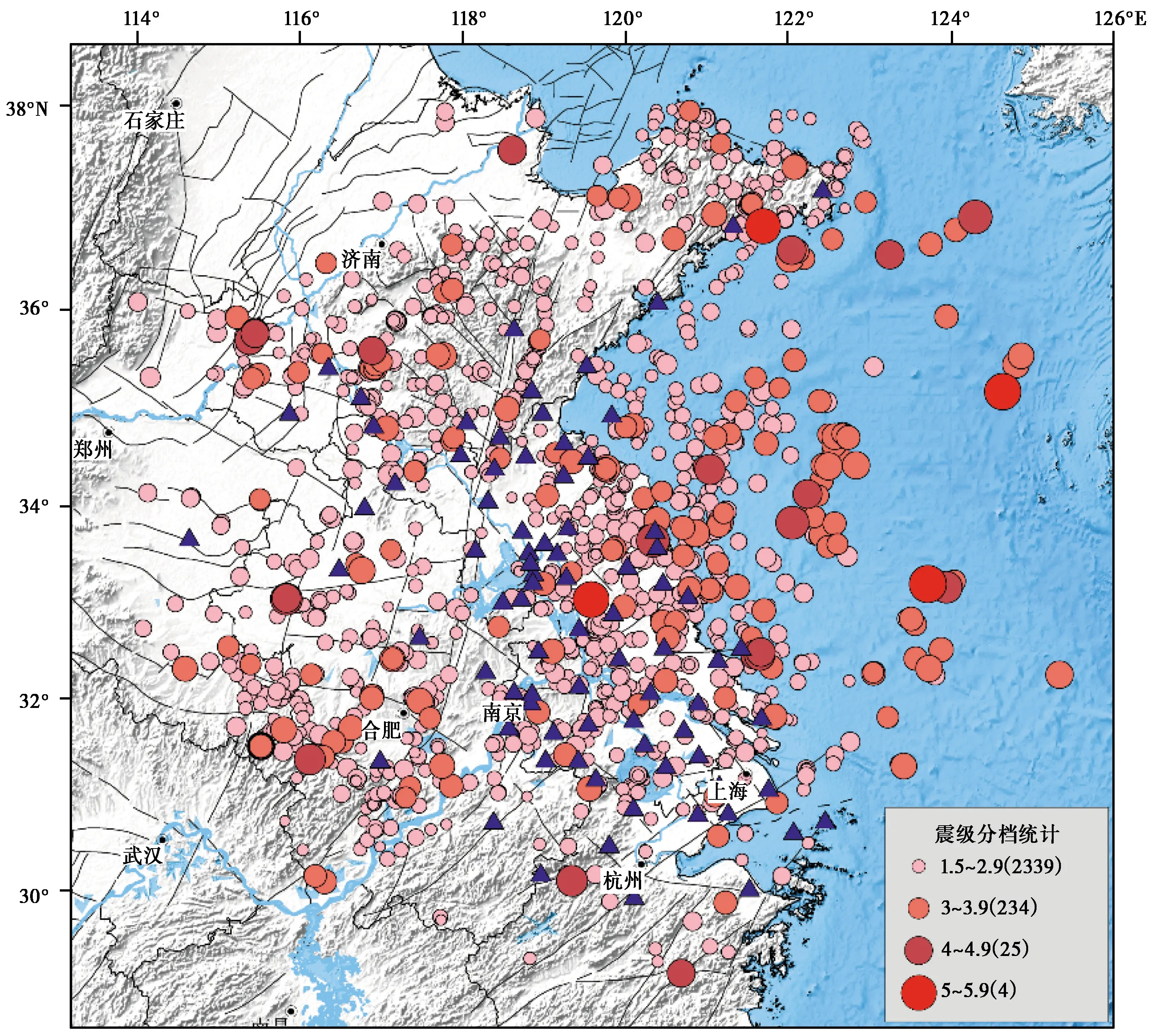
图1 本文选用的台站和地震震中分布

表1 量规函数R12(Δ)

使用广东省地震监测中心开发的交互处理软件JOPENS-MSDP 5.2,利用HYPOSAT方法定位程序(Schweitzer,2001)进行地震定位,采用IASP91全球地壳模型求出发震时刻,继而得到多台平均值,其产出的地方性震级结果使用的是“旧量规函数”中的R2(Δ),而本文在进行震级计算时则利用新震级国标中的量规函数R12(Δ)进行重新计算。考虑到观测资料的质量,剔除由于仪器参数填写错误而导致的单台震级偏差超过2的记录。

2 计算方法

由于目前全国测震台站均为数字化速度型记录,而在速度记录上测定地方性震级容易造成周期值读取的不稳定,为了保证ML震级标度的继承性和统一性,将原始记录的速度振幅值均仿真成伍德-安德森短周期地震仪记录后,量取两水平向最大振幅的位移值,最后采用下式计算各子台地方性震级值,台网震级取多台震级平均值,即

ML=lgAμ+R(Δ)

(1)

式中,Aμ为两水平分向记录的最大地动位移的算术平均值(μm),R(Δ)为我国GB17740—2017《地震震级的规定》中的附录A地方性震级量规函数表(表1)中的量规函数。按照规定,江苏地区使用R12(Δ)。

由于地壳构造的复杂性和不均匀性,地震波通过地壳的过程非常复杂,地震波振幅也千变万化(陈培善等,1983),同时,由于地震波辐射的方向性,处在不同方位的台站震级差可达1.5级甚至更大,因此需要大量的全方位覆盖的地震进行统计分析,以消除地震辐射方向性的差异。震级残差统计方法是指用单台地震的震级值减去该地震的多台震级平均值,得到单台震级偏差,根据震级偏差随震中距的变化曲线,进而得到新的量规函数。

对第j个台站,按式(1)求得单台地震的震级Mij,然后对第i个地震所有记录到的N个子台震级求平均值Mi和标准偏差δi(郭履灿等,1986；陈运泰等,2004),即

(2)

(3)

第i个地震、第j子台震级偏差和平均偏差为

ΔMij=Mij-Mi

(4)

(5)

(6)

式中,k为间隔序数,N为间隔范围内震级偏差样本数。

3 计算结果及分析

对江苏及相邻数字地震台网72个子台所记录的2602个地震共20173个样本数据进行整理统计,采用上述方法,计算得到了各子台震级相对于台网震级Mi的平均偏差ΔMi和标准偏差δi,计算结果见表2。

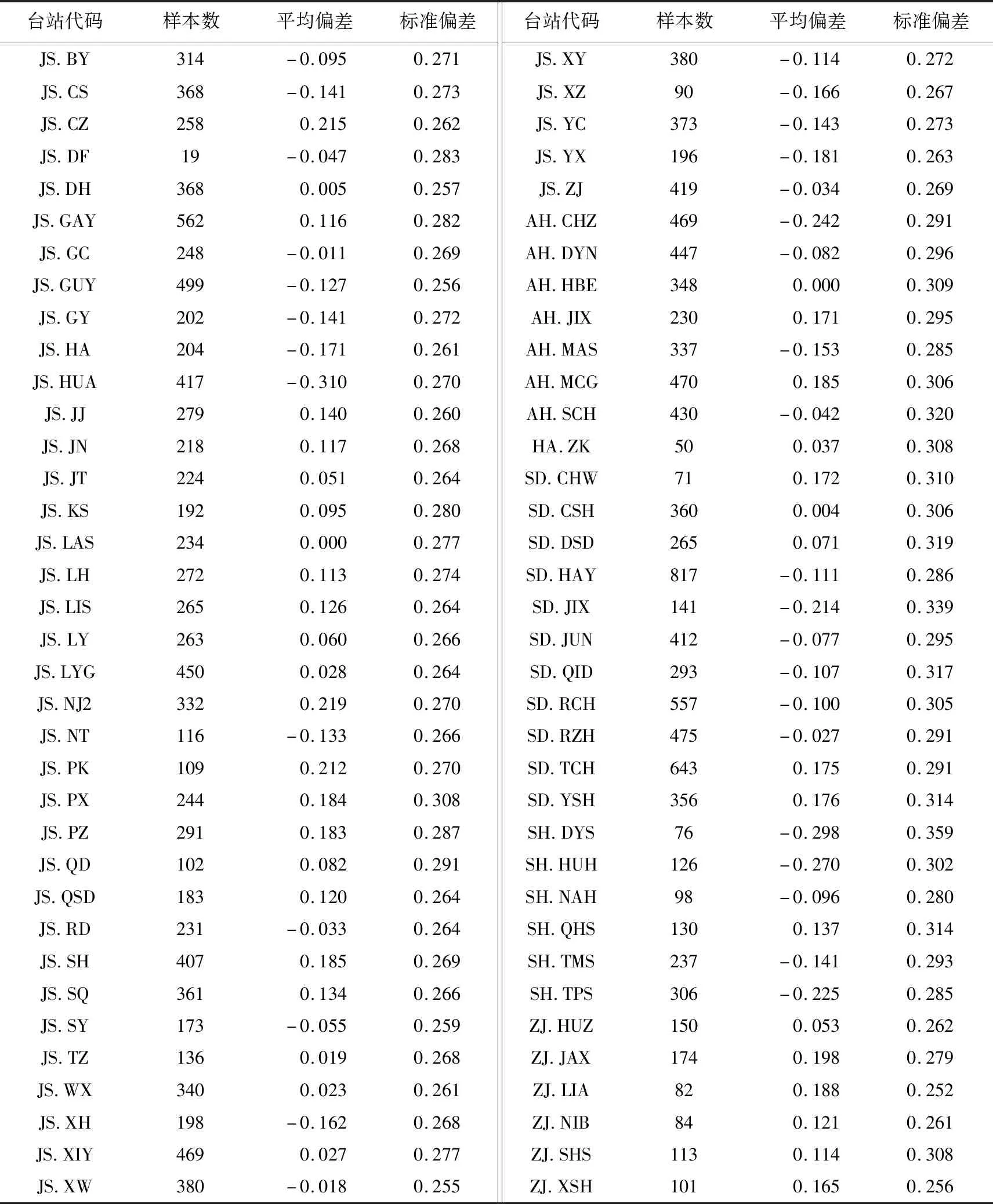
表2 各子台计算得到的平均偏差和标准偏差

3.1 单台震级与台网平均震级的偏差比较

对所有样本进行单台震级与平均震级偏差值的统计,如图2 所示,偏差值基本呈正态分布、相对集中于-0.4～0.4。在20173个单台震级样本中,偏差值(绝对值)在0.2以内(包括0.2)的有13240次,占65.6%；0.2～0.5之间的有6185次,占30.7%；0.5～1.0之间的有733次,占3.6%；大于1.0的有15次,占0.1%。

图2 单台震级与平均震级偏差统计

从表2 中可以看到,多数台站存在震级偏差,偏差范围在-0.31～0.22之间,72个台站中有63个台站的震级平均偏差绝对值在0.2之内,占87.5%；JS.NJ2、JS.PK、JS.CZ、JS.HUA、AH.CHZ、SD.JIX、SH.TPS、SH.DYS和SH.HUH这9个台的震级偏差绝对值超过0.2。其中,JS.NJ2、JS.PK、JS.CZ台为正偏差,该偏差可能来自于场地影响,虽然其台基类型均为基岩,但场地响应值显示偏大2倍左右(康清清等,2016),因此计算出的震级值也普遍偏大。JS.HUA台位于苏中及沿海厚覆盖层区,井下地震计埋深315m,一般来说,虽然松散沉积层对入射波有一定的放大作用(吴微微等,2016),但由于布设台站为井下地震计,其场地响应与其他松散沉积台基类型的井下台站场地响应相比,未呈现出低频部分放大2～5倍的形态特征,而是较为平坦且分布在1附近(康清清等,2016),因此计算出的震级值偏小。SD.JIX、AH.CHZ、SH.TPS、SH.DYS和SH.HUH台计算出的震级值均偏小,这5个外省台站记录的样本地震分布偏于一侧,很可能是受震源辐射的影响,这一现象还有待做进一步的研究。所有台站标准偏差值均在0.25～0.36之间,说明震级偏差值的离散程度较小。

3.2 单台震级偏差值随震中距的变化

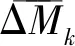
(7)

江苏及邻区震级偏差随震中距的变化曲线如图3 所示。由图3 可以看到,当震中距小于100km时,单台与平均震级的平均偏差值小于0,尤其是震中距在40km以内时,单台震级与平均震级的平均偏差超出了0.15,说明此震中距范围内量规函数偏小；当震中距在100～280km时,震级偏差均在-0.1～0.1之间摆动,表明量规函数是适用的；当震中距在280～450km时,震级偏差均大于0,说明此震中距范围内量规函数偏大；震中距大于450km的资料数量较少,且地震多分布于黄海海域,存在地震波辐射方向的差异,本文不予讨论。

表3 单台震级偏差按震中距分段统计

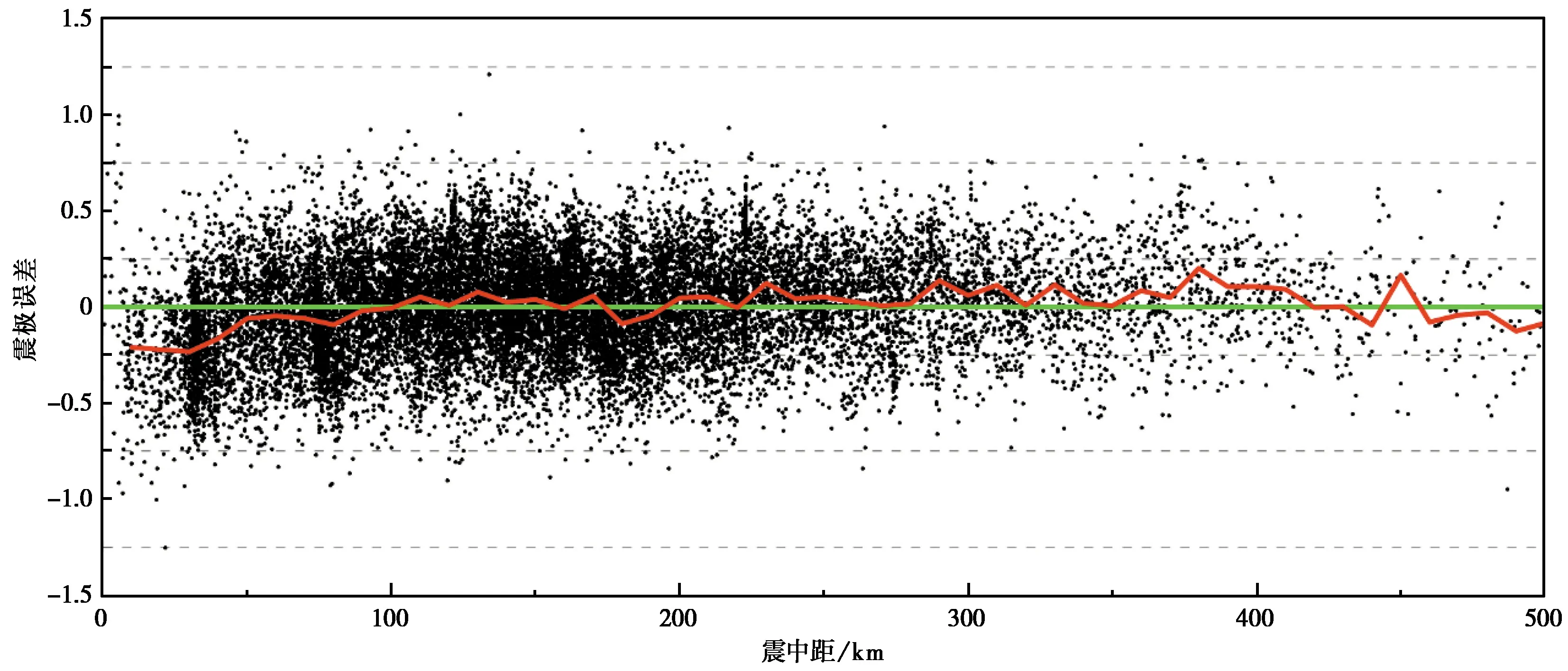
图3 单台震级偏差随震中距的变化图

3.3 量规函数的校正

从图3 可以看出,震中距小于40km的地震,单台震级普遍偏小;震中距在280～450km范围的地震,单台震级普遍偏大,这表明在江苏及邻区震中距450km以内的地震量规函数可以通过校正以更适用于本地区的震级计算。按照式(7)对这一范围内的数据进行校正,校正后的江苏及邻区量规函数R′(Δ)曲线见图4,图4 同时也给出了GB17740—1999和GB17740—2017中用于江苏地区的量规函数曲线,以作对比分析。

图4 量规函数曲线

图4中江苏及邻区校正后的量规函数R′(Δ)曲线在震中距小于40km时,对R12(Δ)曲线改正量较大；新震级国标中R12(Δ)在这一震中距范围内相比R(Δ)略有增大,但还不够补偿地震波随震源距的衰减。这一范围内震级偏差可能是由于震源深度变化引起的,随着震源深度的增加,震源距和震中距之间的差别变大,这就使随震中距变化的量规函数存在较大差别。震中距在100～280km范围时,3种量规函数差别不大。当震中距在280～450km范围时,R′(Δ)比R12(Δ)略小。

4 量规函数的检验

为了检验校正后量规函数的精度和可用性,利用本文选取的2018～2019年江苏及邻区ML≥1.5地震观测资料,采用校正后的量规函数对其震级进行重新测定,并与采用GB17740—2017震级国标中量规函数计算的单台震级偏差和标准误差结果进行对比。得到的单台震级偏差统计结果对比如图5 所示。由图5 可以看出,使用校正后的量规函数R′(Δ)计算所得的单台震级偏差较R12(Δ)更加集中于ΔMij=0的方向,这说明使用校正后的量规函数能减小单台震级偏差。根据式(3)得到单台震级的标准误差,将研究区域内各台站标准误差值求平均值得到区域标准误差,修正前后的区域标准误差分别为0.2768和0.2627,表明利用校正后的量规函数计算得到的震级优于R12(Δ)。综上所述,使用校正后的量规函数能够提高江苏及邻区地方性震级的测定精度。

图5 使用校正后的量规函数R′(Δ)与量规函数R12(Δ)计算所得的单台震级偏差统计对比

5 讨论和结论

选用2009～2018年江苏及邻区测震台网数字地震记录资料,利用震级残差统计分析方法,对区域范围内72个台站的观测数据进行了归类分析,得到单台震级与台网平均震级的偏差值、震级偏差值随震中距的变化和量规函数。除JS.PK、JS.NJ2、JS.CZ、JS.HUA、AH.CHZ、SD.JIX、SH.TPS、SH.DYS和SH.HUH 9个台的震级偏差较大外,有63个台站的震级平均偏差均在±0.2之内,占87.5%。其中,JS.NJ2、JS.PK、JS.CZ、JS.HUA和AN.CHZ台的偏差可能来自于场地影响；SD.JIX、SH.TPS、SH.DYS和SH.HUH台的偏差可能是受震源辐射的影响,这一现象还有待做进一步的研究。

震中距小于100km、尤其是40km以内及震中距在280～450km之间的新量规函数较之前有一定的变化；震中距在100～280km范围时,校正前后量规函数的变化在0.1～0.2之间,变化较小。通过实际测定地方性震级表明,使用校正后的量规函数计算所得的单台震级偏差更加集中,并向ΔMij=0靠拢；且使用校正后量规函数计算所得的地方性震级的标准误差从0.2768减小到0.2627,说明使用校正后的量规函数能够提高本地区地方性震级的测定精度。

致谢：衷心感谢中国地震局地球物理研究所刘瑞丰研究员的启发和指导以及甘肃省地震局陈继峰、四川省地震局吴微微的大力帮助。