基于CEEMDAN-SOBI对桥梁监测挠度的分离研究*
2019-12-12谭冬梅陈方望
谭冬梅,陈方望,周 强,吴 浩
(1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室,湖北 武汉 430070;2.华中师范大学 城市与环境科学学院,湖北 武汉 430079)
0 引言
桥梁结构在运营过程中承受多种荷载作用,因此对结构进行挠度监测得到的实时挠度是多项因素共同作用的结果,据已有研究表明,影响因素主要包括车载、温度作用及混凝土的收缩徐变等[1]。实时监测挠度反映是各项因素共同作用的结果,因此有必要对监测数据进行处理得到各项因素单独作用下桥梁结构的响应。
针对桥梁结构监测挠度的分离问题,目前已有部分学者对监测得到的响应时程数据,提出不同的方法:针对活载效应的分离,梁宗保等[2]研究小波多尺度分解在活载分离的应用。针对温度效应的分离,陈夏春等[3]提出应用多元线性回归模型提取桥梁结构中的温度效应;刘纲等[4-6]分别提出基于粒子群优化算法的自适应滤波方法、最小二乘支持向量机以及多最小二乘支持向量机来获取监测数据的温度效应;孙雅琼等[7-8]通过现场试验确定桥梁结构动应变与温度的关系,提出采用时变多元线性拟合的方法得到温度效应时程曲线;Tang等[9-11]通过传统的经验模态分解(EMD)对信号进行升维,然后进行独立分量分析;谭冬梅等[12-13]分别采用改进PCA算法结合集成经验模态分解(EEMD)和MEEMD对实测挠度的日温差效应进行分离。针对各挠度成分的分离,刘夏平等[14]研究了基于奇异值分解的盲信号分离方法;陈国良等[15]结合时间小波分解和时间序列分析中的中心移动平均法分解得出各成分挠度。
本文针对各挠度成分的分离,提出1种基于CEEMDAN-SOBI的挠度成分分离算法。首先利用CEEMDAN将单通道多源的挠度信号分解为一系列IMF分量,减轻了传统EMD和EEMD在分解时的模态混叠问题;然后利用排列熵算法对分解得到的各分量进行排列熵值计算,将排列熵值接近的分量重组得到新的分量,采用基于K-L散度的虚假分量判别法识别并剔除重组分量中虚假重组分量,避免直接基于K-L散度剔除虚假模态容易产生的过度剔除。
1 基本理论
1.1 CEEMDAN算法
CEEMDAN算法由TORRES[16]等提出,相比EMD和EEMD算法[17],该算法更好抑制了模态混叠的问题,可消除IMF分量中的噪声,自适应获取集成平均次数和噪声幅值,提高计算速度[18]。CEEMDAN算法步骤如下:

1)对于第1阶IMF分量,其求取方法与EEMD分解方法一致,对原始信号x(t)添加不同的噪声I次,利用EMD分解I次并求取平均值得到IMF1(t):
(1)
2)计算第1个残余量信号R1(t):
R1(t)=x(t)-IMF1(t)
(2)
3)对信号R1(t)+ε1Ei(ni(t))进行N次EMD分解,得到第2个IMF分量:
(3)
4)对于k∈[2,K],依次计算第k个残余信号Rk(t):
Rk(t)=Rk-1(t)-IMFk(t)
(4)
5)对于每一个Rk(t),重复步骤3)的过程,得到第k+1个IMF分量为:
(5)
6)重复上述步骤,当残差信号不能再被继续分解时,得到最终残差R(t):
(6)
由此可得各阶IMF分量IMFk(t)和R(t)。
1.2 排列熵
排列熵是用来判断时间序列复杂程度的1种方式,相比其他常用方法,该方法计算效率高、对噪声的鲁棒性更好[19-20]。序列的排列熵计算步骤如下:
1)已知原始序列z(n)(n=1,2,…,N),设定维数为m,时间延时为τ,嵌入维度m的取值一般为3~7,嵌入时延τ的取值一般为1。将z(n)构造成如下式矩阵:

(7)
式中:M=N-(m-1)τ,M是矩阵的行数。
2)将矩阵中每1行视为1个向量zj={z(j),z(j+τ),…,z(j+(m-1)τ)},其中j=1,2,…,M,将向量中元素值的大小按照升序排列如下:
z(j+(j1-1)τ)≤…≤z(j+(jm-1)τ)
(8)
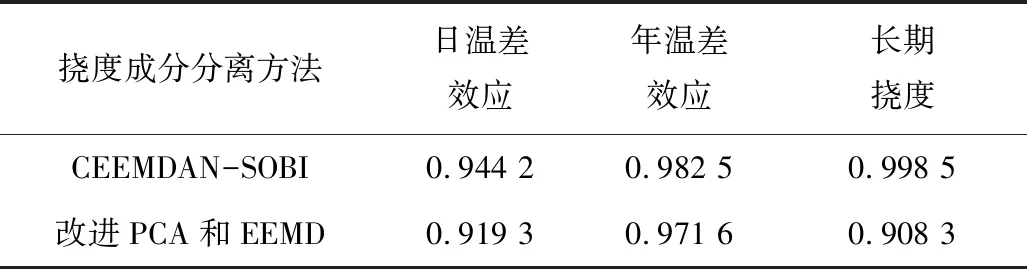
式中:j1,j2,…,jm为向量zj中每个元素在排序前的索引号,对于向量中元素值大小相等的情况,即若jp 3)对于每一个向量zj都对应1个符号向量sj={j1,j2,…,jm},设1个m维重构相空间对应的符号序列的概率密度分别为P1,P2,…,Pk,则对于一维时间序列z(n)的M个重构向量对应的符号序列,排列熵可表示为: (9) 序列的排列熵值表征了序列的复杂程度,排列熵值越大,则序列越复杂。 在概率论和信息论中K-L散度[21]也称之为相对熵,其是对2个概率分布P与Q之间关系的描述,定义为: (10) (11) (12) 式中:P(y)为密度函数的核密度估计;K(·)为核函数;h为给定的正数,通常称为窗宽或平滑参数。在实际情况下,信号的分布是单峰和对称的,由上式可得到对称形式下P和Q之间的K-L散度的定义: D(P,Q)=DKL(P||Q)+DKL(Q||P) (13) 在虚假IMF分量识别过程中,K-L散度表征了单通道混合信号与各分量之间关系的紧密程度,K-L散度越小,则分量与原混合信号的关系越紧密,该分量为信号的真实成分,反之关系越疏远,该分量为需剔除的虚假分量。 1)计算白化矩阵W,白化矩阵W可根据观测信号的自相关矩阵的特征值分解得到: (14) 式中:λ1,λ2,…,λn为原始数据零均值化后的自相关矩阵的n个最大特征值;h1,h2,…,hn分别为特征值对应的特征向量;σ2是噪声的方差。 2)白化后的信号为: Z(t)=WX(t) (15) 3)计算观测信号白化后的采样协方差矩阵R(τ): R(τ)=E[Z(t+τ)ZT(t)]=ARZ(τ)AT (16) τ∈{τj|j=1,2,…,k} (17) 4)计算正交矩阵U,对于所有的R(τj),采用联合近似对角化算法,得出正交矩阵U满足: UTR(τj)U=Dj (18) 式中:Dj是1组对角矩阵。 5)计算分离矩阵和分离信号,混合矩阵A=W-1U,所以分离矩阵B=A-1=UTW,分离信号: Y(t)=UTWX(t) (19) 挠度分离的步骤: 2)计算每个分量的排列熵,将排列熵值相近的分量相加,组成新的一系列分量; 桥梁在运营过程中的温度效应的挠度信号主要由日温差及年温差组成,桥梁运营过程中还会由于预应力损失及混凝土收缩徐变而引起长期挠度。为更好模拟桥梁挠度信号,在Midas Civil软件上建立武汉某斜拉桥有限元模型并对结构仿真分析,模型如图1所示,模拟桥梁挠度信号可表示为: 图1 武汉某斜拉桥模型Fig.1 Model of a cable-stayed bridge in Wuhan f(t)=f1(t)+f2(t)+f3(t) (20) 式中:f(t)为总体挠度信号,mm;f1(t)为日温差效应,mm,f1(t)=f11(t)+f12(t),f11(t)整体温差效应,mm,f12(t)为截面日温差效应,mm;f2(t)为年温差效应,mm;f3(t)为长期挠度,mm。 对于温度作用下挠度信号的模拟,桥梁模型整体升温1 ℃,跨中向下产生1.86 mm偏移;整体降温1 ℃,跨中向上产生1.86 mm偏移;主梁截面线性增加温差1 ℃,跨中向下产生0.54 mm偏移。假定日温差和年温差均为正弦变化的周期性函数,其中整体日温差和截面日温差共同组成日温差,取每日的整体日温差10 ℃,截面日温差5 ℃以及年温差30 ℃。由此可得,整体日温差f11(t)=9.3sin(πt/24),截面日温差f12(t)=1.35sin(πt/24),年温差f2(t)=27.9sin(πt/8 760)。 对于长期挠度的模拟,参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018),用指数型函数拟合得到长期挠度[13]。各成分挠度信号及总体桥梁挠度模拟信号如图2所示,为显示方便,日温差选取前5 000 h内数据绘图。 图2 各成分模拟信号及总挠度模拟信号Fig.2 Simulation signals of each component and total deflection 依据拟定分解流程,对原始信号通过CEEMDAN分解得到13个不同尺度特征的模态分量IMF和1个残余项R,CEEMDAN算法在一定程度上减轻了EEMD的模态混叠问题,但仍存在一定的模态混叠问题,故需进行进一步处理[15-16]。首先计算各分量的排列熵,将排列熵值相近的分量相加得到重组分量,再结合K-L散度剔除虚假的重组分量。各分量排列熵值如图3所示,由图3可知,各分量排列熵值随着分量频率的减小而逐渐降低,即频率低的分量复杂度越低,以各分量排列熵值大小为标准对各分量进行重组。图3中,IMF1和IMF2的排列熵值明显大于其他所有分量,且熵值相近,故将两者相加作为1个新的分量CF1;IMF3,IMF4,IMF5的PE值相差为0.005左右,复杂度相似,故可将三者相加得到新的分量CF2;同理将IMF6,IMF7,IMF8合并为CF3;将IMF9,IMF10,IMF11,IMF12,IMF13合并为CF4;残余项R的PE值最小,作为重组分量CF5。 图3 各分量的排列熵值Fig.3 Permutation entropy of each component 对于分解重组得到的分量中必然存在部分虚假分量,本文基于K-L散度理论剔除虚假分量。首先计算各分量与原始信号的K-L散度值,结果如图4所示,由图4可知,重组分量CF2,CF4,CF5的K-L散度值最小,故选择CF2,CF4,CF5作为原始信号的主要成分,其他的予以剔除;最后基于SOBI原理,对提取出来的CF2,CF4,CF5组合为高维矩阵分析,估计原始信号,得到分离结果如图5所示,为显示方便,日温差分离结果选取前5 000 h内数据绘图。 图4 基于K-L散度的虚假模态识别Fig.4 False modal recognition based on K-L divergence 图5 基于SOBI原理的信号分离结果Fig.5 Signal separation results based on SOBI principle 对于分离结果的效果评价,采用分离结果与原始信号间的相关系数及平均绝对误差来评价,两者分别如下定义: 相关系数: (21) 平均绝对误差: (22) 表1 各成分分离结果的评价指标Table 1 Evaluation indexes for separation results of each component 武汉某斜拉桥在运营中结合北斗定位导航技术,对其主体结构的三维变形进行实时监测。北斗监测系统较传统监测方式,具有精度较高、不受气候条件影响且实时高效率等特点,桥面测点布置如图6所示。 图6 武汉某斜拉桥主桥监测测点布置Fig.6 Layout of monitoring points on main bridge of a cable-stayed bridge in Wuhan 考虑相邻测点布置处的桥面受到温度作用的影响基本相近,两相邻测点记录的挠度数据中温度效应及长期挠度的变化趋势应具有较强的相关性。故对于实测数据的分离效果评价可通过对称测点分离结果间的相关性来评价。 为验证本文方法在实际应用中的有效性,采集背景桥梁实时监测挠度1年内的数据,利用CEEMDAN-SOBI对桥梁的各挠度成分进行分离。采集测点编号为BD12和BD35,采集时间段为2017年9月1日00:00:00至2018年8月1日00:00:00,采样频率为1 h/次,采集得到的挠度监测数据如图7所示。为避免部分随机脉冲噪声对后续分解的影响,先对原始信号进行高斯平滑,去除异常点,再对信号进行分离。日温差效应分离结果如图8所示;年温差效应分离结果如图9所示;长期挠度分离结果如图10所示。 图7 动挠度实测数据Fig.7 Measured data of dynamic deflection 图8 日温差效应分离结果Fig.8 Separation results of daily temperature difference effect 图9 年温差效应分离结果Fig.9 Separation results of annual temperature difference effect 图10 长期挠度分离结果Fig.10 Separation results of long-term deflection 从图8~10可知,所选跨中对称测点BD12和BD35在1年内日温差效应、年温差效应及长期挠度变化趋势具有很明显的相似性,分别计算基于CEEMDAN-SOBI与改进PCA和EEMD[12]方法得到的2测点各挠度成分的分离结果之间的相关系数,如表2所示。从表2可知,各成分间相关系数均较高,证明本文所提方法能较好分离得到实际工程中监测挠度的各成分,且计算精度要优于改进PCA和EEMD方法。 表2 测点BD12和BD35的实测挠度各成分分离结果间的相关系数Table 2 Correlation coefficient between separation results of each component for measured deflection at measuring points BD12 and BD35 1)CEEMDAN减轻了传统EMD和EEMD算法分解信号产生的模态混叠问题,采用排列熵结合K-L散度剔除虚假分量减轻了直接基于K-L散度剔除虚假分量容易产生的过度剔除问题。 2)将CEEMDAN-SOBI算法应用到模拟信号和实测信号的分离,模拟信号分离结果显示分离值与实际值的相关性及平均绝对误差趋于理想值;主跨跨中对称测点实测信号各成分分离结果具有较高的相关性,均在0.94以上,验证了CEEMDAN-SOBI算法在分离实际桥梁监测挠度各成分的有效性;对比分析了本文计算方法和已有方法对挠度信号的分离效果,结果表明本文方法具有更高精度。 3)本文所提方法是以各效应值时间尺度上的差异为基本条件的,桥梁结构实际运营中,车辆堵车条件下缓慢通行以及积雪等形成的具有与温度变化尺度相近的荷载会对温度挠度的准确分离产生一定的干扰,有必要对之监控并剔除。本文提出的方法还可以应用于桥梁长期监测系统中索力和应变的各效应值的分离。1.3 K-L散度
1.4 SOBI算法原理

1.5 挠度信号分离流程

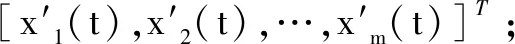

2 桥梁模拟挠度信号分离
2.1 挠度信号模拟

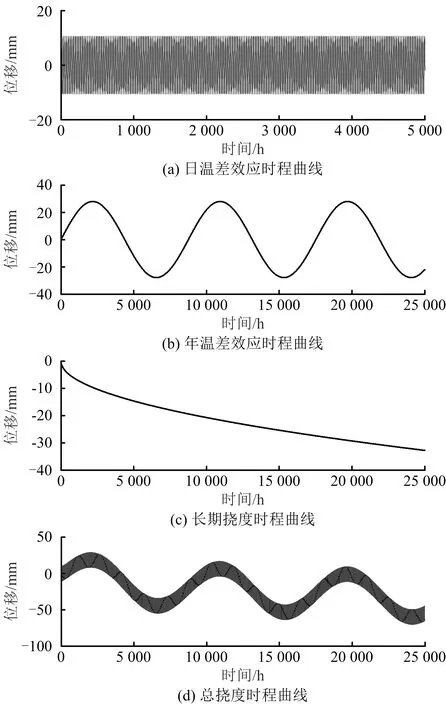
2.2 挠度信号分离





3 实测桥梁挠度信号成分分离
3.1 工程背景
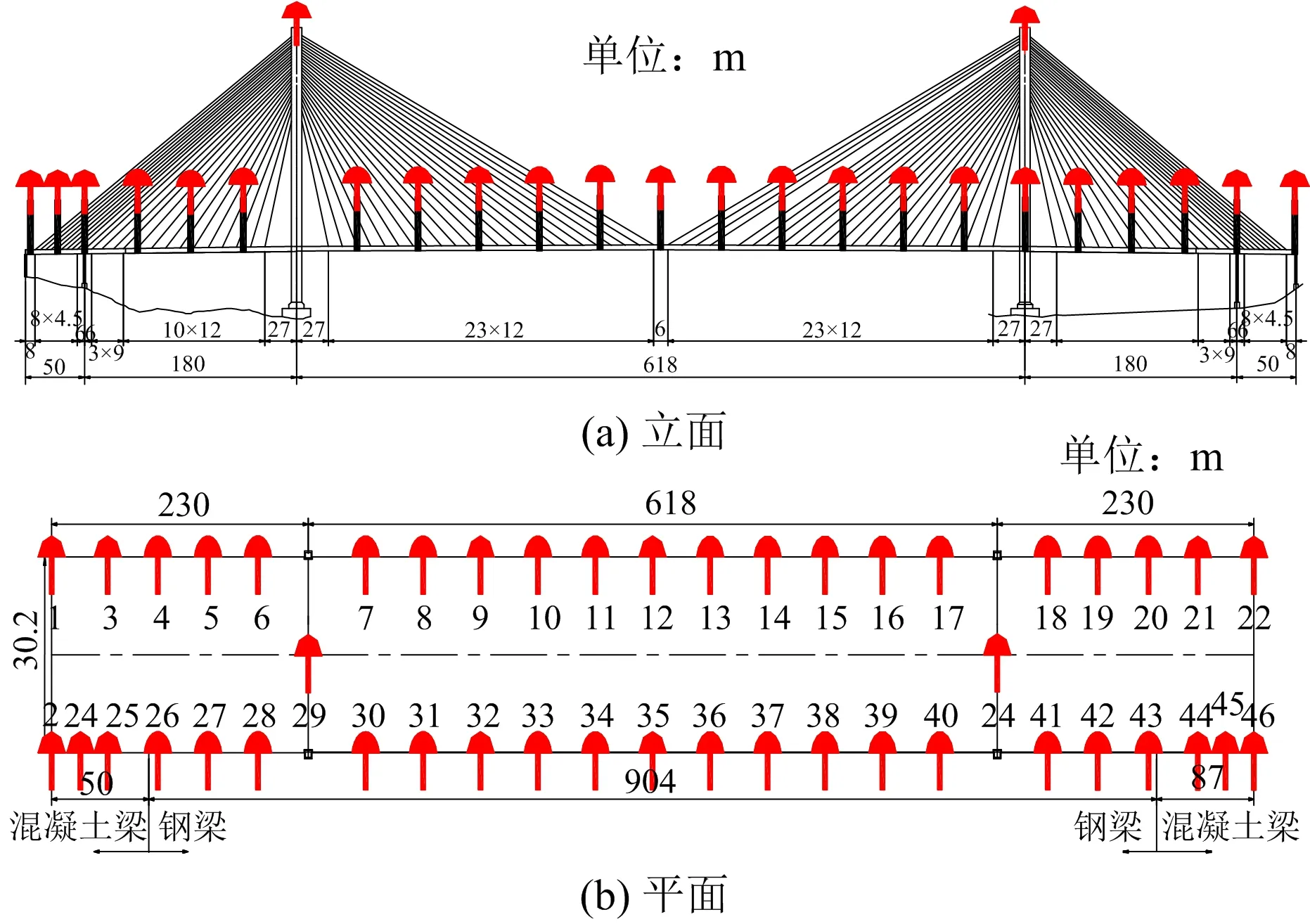
3.2 实测挠度信号的各成分分离



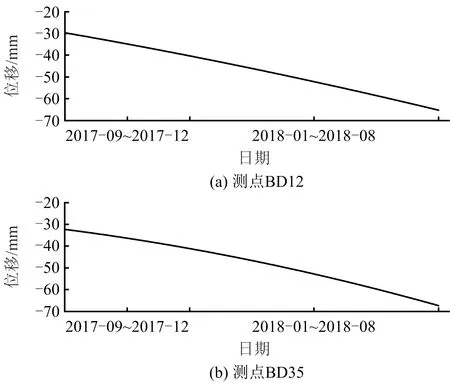
4 结论
