利用形态滤波去ECG基线漂移的简单方法

徐万松 川北医学院 医学影像学院 （四川 南充 637000）

内容提要： 心电信号（ECG）在进行自动处理前一般要经过去基线漂移等预处理。去ECG基线漂移方法较多，文章利用形态滤波的方法，根据心电信号中各特征波形的时间宽度，选择合适尺寸的结构元素对含基漂ECG信号进行滤波处理，滤除QRS波群及P、T波等特征波形，然后利用平滑滤波得到基漂信号，最后利用原始ECG信号减去基漂信号，从而去除基线漂移。该算法计算简单、实时性好，在Matlab平台上经过MIT-BIH数据库中实际ECG信号的验证，去基线漂移效果较好。

心电信号（ECG）由于呼吸运动、电极与皮肤之间接触阻抗以及放大器温漂等因素影响，会产生基线漂移。基线漂移一般是频响小于1Hz的低频扰动，通常表现为缓慢变化的曲线，它对ECG信号的正确分析和自动处理有较大影响，应在心电信号预处理中予以消除。根据目前资料来看，采用基于数学形态学的形态滤波算法的方法去基线漂移效果较好[1]。

1.数学形态学滤波器

1.1 数学形态学

数学形态学（Mathematical Morphology）是一门建立在格论和拓扑学基础之上的图像分析学科，其基本的运算包括：腐蚀和膨胀、开运算和闭运算、骨架抽取等。数学形态学方法利用一个称作结构元素的“探针”收集图像的信息，当探针在图像中不断移动时，便可考察图像各个部分之间的相互关系，从而了解图像的结构特征。

1.2 腐蚀和膨胀

腐蚀和膨胀是数学形态学中最基本的运算。其他更为复杂的形态学运算都可通过它们来定义。由于心电信号是一维信号，这里简述定义在一维信号处理中的腐蚀和膨胀。

设f(n)，(n=0,1…N-1)和k(m)，(m=0,1…M-1)为一维离散函数，且N≫M。其中f(n)为待处理信号序列，k(m)为结构元素。

腐蚀是取结构元素与信号的最大相关点集。f(n)关于k(n)的腐蚀运算定义为公式（1）：

注：n=(0,1,…N-M)

膨胀是腐蚀的对偶运算（逆运算）。f(n)关于k(n)的膨胀运算定义为公式（2）：

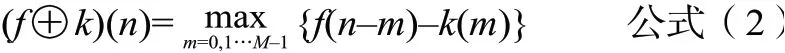
注：n=(M-1,M,N-1)

1.3 开运算和闭运算

开、闭运算是形态学的二次运算，由腐蚀和膨胀这两种运算的级联得到。

f(n)关于k(n)的开运算定义为公式（3）：

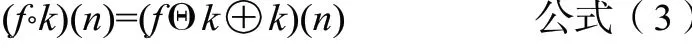
f(n)关于k(n)的闭运算定义为公式（4）：

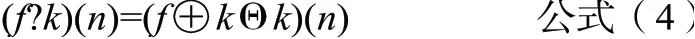
开运算和闭运算分别是在信号的下方和上方移动结构元素，并在每一点记录结构元素的最高点和最低点。开运算可消去信号中的波峰，闭运算可填充信号中的波谷。

1.4 形态学滤波器设计

形态滤波器的实质是通过组合运用开、闭运算，消除信号中特定宽度的波峰、波谷。信号中实际被滤除的成分与运算中所采用的结构元素有关[2]。由于开运算的收缩性使得开闭滤波器的输出幅值较小，闭运算的扩张性使得闭开滤波器的输出幅值较大，为了有效抑制单向偏移，采用这两种滤波器的组合形式。即公式（5）：

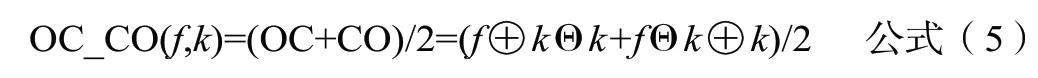
结构元素的选取在形态滤波器的设计中非常重要，不同的形状和尺寸都会影响形态变换的性能。一般而言结构元素的形状要尽可能接近待分析信号的图形特点，结构元素的尺寸应大于被滤信号的尺寸，而小于被保留信号的尺寸[3]。

2.ECG信号的基线消除方法

2.1 ECG信号特点

典型的ECG波形如图1所示，主要由P波、QRS波群和T波等典型特征波形组成。临床实测的ECG信号可看作是特征波形与缓变基线漂移信号叠加而成。

不同于杂乱无章的脉冲噪声，ECG信号波形有特定变化规律，一般地QRS波群振幅高而占时短（0.6～0.10s），P波（0.08～0.11s）和T波（0.05～0.25s）振幅低而时间较长，具体时间宽度因人而异。

2.2 基于形态滤波消除基线漂移算法框架流程

ECG信号可看作是特征波形与缓变基线漂移信号的叠加，可先分离出基漂信号再做减法处理。具体而言，首先采用宽度较大的结构元素，通过一系列的开、闭运算，滤除QRS波群及P波、T波，得到基线漂移信号；然后对基漂信号作平滑处理；最后将源ECG信号与缓变基漂信号做减法处理，从而得到去除基线漂移的ECG信号。算法流程图如图2所示。

图1. 典型ECG 波形特征波形

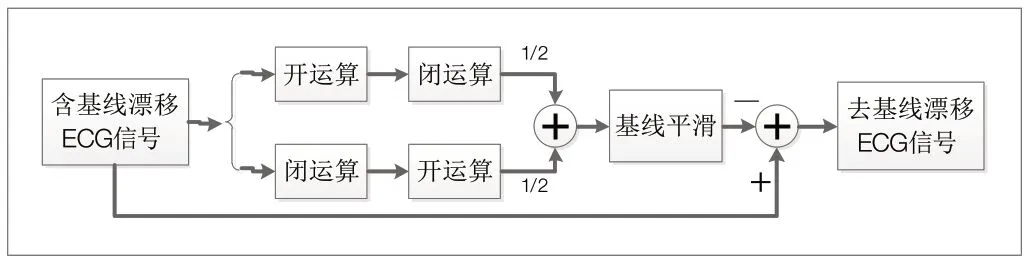
图2. ECG 去基线漂移信号处理流程图

2.2.1 去QRS、P、T波特征波形

一般情况下QRS波群及P波的时间宽度相当，因此滤除QRS波群和P波特征波形可同时进行，而T波一般较宽，因此进行形态滤波时其结构元素的宽度选择尤为重要，一方面算法对于不同个体的ECG心电信号处理具有较强的鲁棒性，另一方面也要求失真尽量小。这里选择结构元素宽度与较宽的T波相当，一方面综合考虑了同时滤除QRS波群、P波、T波等特征波形，另一方面兼顾较小的失真。这里采用具有代表性的MIT-BIH数据库中的ECG数据（第115号数据），其采样率Fs=360。而QRS波群、P波的时间宽度相当，若宽度选择过小会造成滤波不充分，太大则容易引起失真，因此选择时间宽度T=0.25s，即形态滤波器结构元素宽度M1=360×0.25≈90。

由于开运算的收缩性使得ECG信号经开-闭滤波处理后信号幅度变小，而闭运算的扩张性使得ECG信号经闭-开滤波器处理后信号幅度变大。为了抑制信号的单向漂移，宜采用这两种滤波器的综合形式。原始含基漂的ECG信号和经过去QRS波、P波、T波等特征波得到的波形分别如图3所示。

2.2.2 基漂信号拟合

对于一维信号滤波而言，所采用的扁平结构元素的长度对波形的平滑程度有较大影响。一般地在一定范围内随着扁平结构元素长度的增加，波形变得更平滑，亦即波形突变更少。对于本文所讨论的ECG信号形态滤波而言，结构元素的宽度选择受限于待滤除波形（如QRS波群、P波、T波宽度），导致滤波处理后得到的基漂信号突变严重，该基漂信号内高频成分较多。而如前文所述，基线漂移为低频缓慢变化，因此这里对含波形突变的基漂信号作平滑处理，以期得到平滑、缓变的基漂信号。这里采用滑动平均法，滑动窗口宽度为100。经过平滑处理后的基漂信号如图4（a）所示。

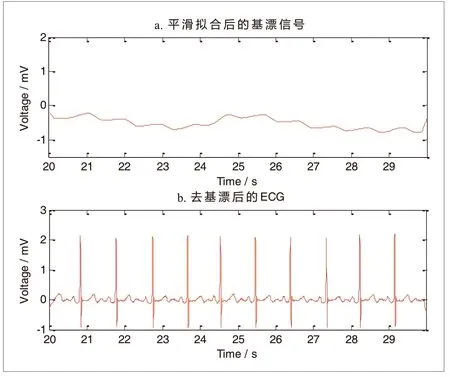
图4. 提取的基漂信号（a）和去基线漂移后的信号（b）

2.2.3 ECG去基漂

ECG信号可看作为特征波形与基漂信号的叠加，如将ECG信号减去前面处理得到的平滑基漂信号，即完成去基线漂移，得到的波形如图4（b）所示。

3.小总

去基线漂移是ECG信号处理中非常重要的一个步骤，对于后续波形分析做铺垫。随着心电采集设备的小型化，智慧医疗、远程医疗迅速发展、自动化程度越来越高，心电等信号的自动化处理要求越来越高，要求实时处理ECG信号[4]。去ECG基线漂移的研究较多，基于形态滤波的方法原理简单，只涉及到一些加减法，计算量小；基于形态学处理算法的鲁棒性较好，去基漂效果好，受到较多关注。本文对以往算法进行了简化，不但有效还原了基漂信号，而且计算量小，适合实时处理。