舵机电位器的反馈位置误差补偿方法研究

郭凯红，高炳东，陈 硕，庞喜浪，熊官送，王 军

(1.海军装备部装备审价中心，北京 100074；2.北京自动化控制设备研究所，北京 100074)

0 引言

导弹用舵机作为执行机构，操纵舵面偏转，同时反馈舵面偏角，保证了导弹主动飞行段的制导和稳定。

电位器是一种将位置或角度转换为一定函数关系电压输出的传感器，由于具备低成本、高可靠、易配置等特点，常作为监测舵面偏角的位置传感器[1-3]，其性能的好坏直接影响导弹制导精度的优劣[4]。然而，电位器基准电压线性误差[5]、负载效应非线性误差[6-7]等因素均能产生反馈位置误差，即舵面偏角误差。在现有线性控制分配方法下，气动舵面产生的力和力矩与舵面偏角在一定范围内呈线性相关，舵面偏角误差将导致导弹发射、大机动飞行时控制效率降低[8]，甚至影响到控制系统回路的稳定性。

文献[9-10]利用2个独立约瑟夫逊电压基准(Josephson Voltage Standard，JVS)减小了电位器基准电压线性误差，实现了高精度任意电压输出，但JVS硬件装置极其复杂，工程上难以实现。文献[11]选用低阻抗电位器并使其工作在零位附近较小行程内，以减小负载效应非线性误差，但功耗提高且精度降低。

本文基于电位器等效电路模型，对电位器基准电压线性误差和负载效应非线性误差展开机理分析和实验验证，提出了一种舵机电位器的反馈位置误差补偿方法，对AD芯片采集的基准电压和实际反馈位置进行解算，得到了基准电压线性误差补偿系数和负载效应非线性误差补偿系数，实现了舵面偏角的有效修正，且成本低，易于工程应用。

1 电位器等效电路模型分析

电位器的拓扑结构类似于滑动变阻器，理想等效电路模型如图1所示[12-13]。在电刷滑动的过程中，电位器阻抗划分为(1-k)R和kR互补的两部分，对A、B这2个基准电压进行分压，反馈电刷位置电压。

(a)

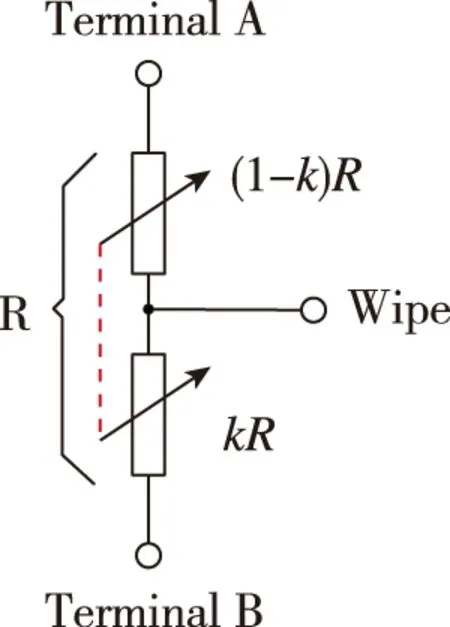
(b)

实际应用的电位器输出阻抗范围并非无穷小值，后级输入阻抗RL也并非无穷大值，电位器存在负载非线性效应，其输出量受到负载的非线性影响。考虑负载效应的电位器等效电路模型如图2所示。

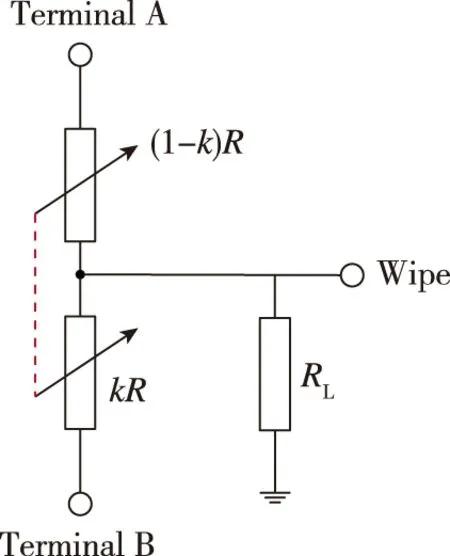
图2 考虑负载效应的电位器等效电路模型Fig.2 Potentiometers’ equivalent circuit model considering load effect

2 电位器反馈位置误差分析及验证

由图2模型可知，电位器反馈位置误差主要为：1)电位器基准电压线性误差；2)电位器负载效应非线性误差[14-15]。以下做简要分析并进行实验验证。

2.1 电位器基准电压线性误差

电位器基准电压作为反馈位置解算的基准[16]，其波动将导致解算结果发生线性变化。

在理想情况下，以±Vin为基准电压、±Ran为工作量程的电位器反馈位置θ解算式为

(1)

其中，Vout为反馈位置电压。

考虑基准电压线性误差的反馈位置θlin解算式为

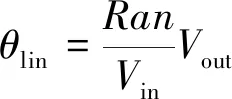
(2)

其中，ΔV1和ΔV2分别表示基准电压+Vin和-Vin的波动量。

因此，电位器基准电压线性误差Errlin解算式为

Errlin=θlin-θ

(3)

在Vin=15V，Ran=150°，Vout=0V的实际工况下，基准电压线性误差Errlin与基准电压波动量(ΔV1、ΔV2)的关系曲线如图3所示。零位处的基准电压线性误差来源于基准电压+Vin和-Vin的不对称波动。当+Vin增大至15.1V，-Vin升至-14.9V时，零位位置误差为1°；当+Vin增大至16.0V，-Vin升至-14.0V时，零位位置误差为10°。

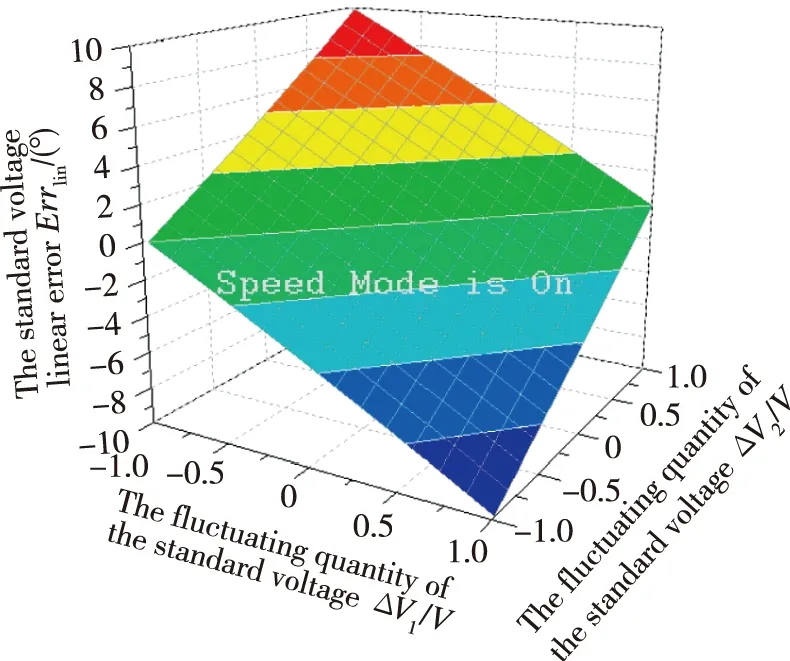
图3 零位处的基准电压线性误差曲线Fig.3 The curve of reference voltage linear error at zero-point

2.2 电位器负载效应非线性误差

由于电位器输出阻抗与后级输入阻抗直接相连产生耦合，只有当后级输入阻抗与电位器输出阻抗之比为无穷大时，电位器的负载特性才是绝对线性的。两电阻之比越小，非线性越严重。

考虑电源模块内阻，电位器负载效应示意图如图4所示。其中，r1和r2分别为电源模块+Vin和-Vin对GND的内阻。

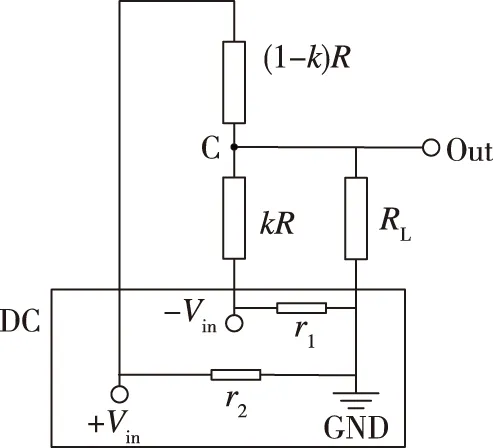
图4 电位器负载效应示意图Fig.4 The schematic diagram of potentiometers’ load effect

当电刷位置C处电势为正时，如图5(a) 所示，电流由+Vin端流至点C，由点C分流分别流经kR和RL后汇聚于-Vin。在负载RL的影响下，对+Vin和-Vin进行分压的并非(1-k)R和kR，而是(1-k)R和kR//(RL+r1)。同理，当电刷位置C处电势为负时，如图5(b) 所示，对+Vin和-Vin进行分压的是[(1-k)R]//(RL+r1)和kR。

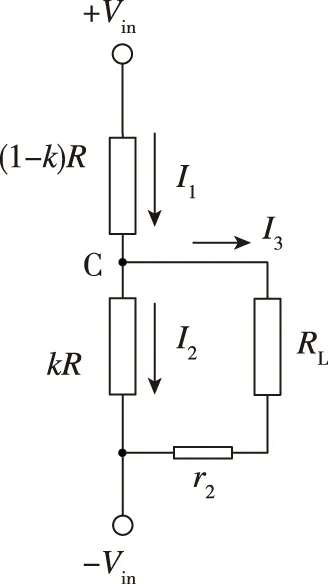
(a)

(b)

在节点C利用基尔霍夫电流定律，可列

(4)

代入后，均得到

(5)

反馈位置电压Vout为

(6)

由式(1)，考虑负载效应非线性误差的反馈位置θnol为

(7)

因此，电位器负载效应非线性误差Errnol解算式为

Errnol=θnol-θ

(8)

在Vin=15V，Ran=150°，R=2.2kΩ的实际工况下，选用典型AD转换芯片AD7943，其输入阻抗RL为9kΩ，负载效应非线性误差曲线如图6所示。负载效应非线性误差以零位中心对称分布，在零位和两端时，非线性位置误差为0；在k=0.79时，非线性位置误差最大，最大值为3.39°。

图6 负载效应非线性误差曲线Fig.6 The curve of load effect nonlinear error

2.3 电位器误差分析结果实验验证

以电位器的应用情况为例，选用基准电压为±15V，随负载波动至 ±14.4V；选用电位器量程为±150°、总阻抗为2.2kΩ；选用AD转换芯片为AD7943，其采样输入阻抗为9kΩ。

理想情况下的反馈位置输出为

θ=(2k-1)Ran

(9)

考虑基准电压线性误差和负载效应非线性误差的反馈位置θlin+nol为

θlin+nol=klinknolθ

(10)

其中，klin为基准电压线性误差系数，定义式为

klin=(Vin+ΔV1)/Vin

(11)

knol为负载效应非线性误差系数，定义式为

knol=1/((1-k)kR/RL+1)

(12)

因此，反馈位置误差Errlin+nol解算式为

Errlin+nol=θlin+nol-θ

(13)

在舵面偏角范围±20°(即0.433≤k≤ 0.567)内，通过高精度转角指示器对舵面偏角进行实测，将舵面偏角折算为电刷位置，与上述分析进行对比，曲线如图7所示。

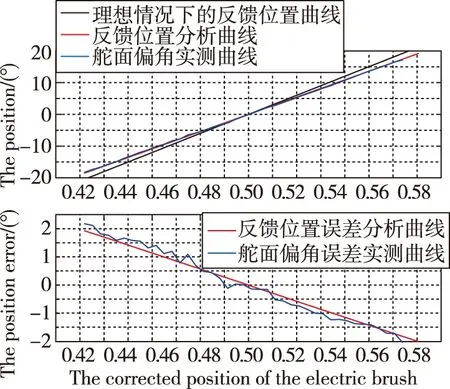
图7 反馈位置误差分析和实测对比图Fig.7 Feedback position error analysis and measurement comparison diagram

通过数据分析可知，将ΔV1和RL设定为可变参数，迭代区间分别为 [-1,1] 和 [1,3] ，对舵面偏角实测曲线按式(10)进行拟合，选取标准差和拟合度为评价标准，拟合结果为：ΔV1=-0.5705V，标准差σΔV1=0.0018，RL=9.2304，标准差为σRL=0.02104，拟合度R2=99.987%。

因此，分析结果和实测结果较为匹配，表明了理论分析结果置信度较高。

3 电位器反馈位置误差补偿方法

本文提出的舵机电位器的反馈位置误差补偿方法，首先通过补偿电路使两端基准电压波动基本对称，然后根据上述机理分析进行算法补偿，对反馈位置做适当修正达到误差补偿的目的。

问题描述：对θlin+nol进行补偿，使θlin+nol-θ满足工程需求。

补偿方法描述：

1)在基准电压上各串联一个负载，如图8所示，以减小电刷移动造成基准电压不对称波动。

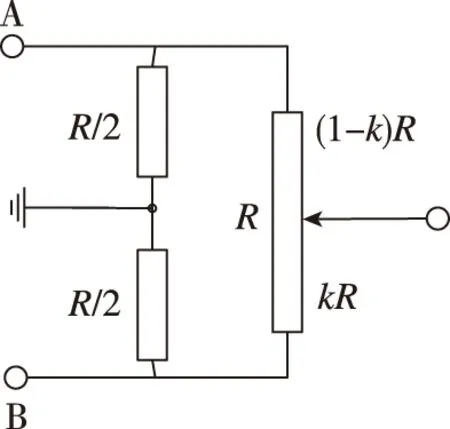
图8 基准电压的负载不对称补偿电路Fig.8 Load unsymmetrical compensation circuit of reference voltage

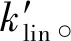
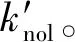
(14)

5)由式(15)得到补偿后电位器反馈位置

(15)

4 实验验证

为验证本文提出的舵机电位器反馈位置误差补偿方法的有效性，开展了补偿方法验证工作。

应用上述补偿方法，通过高精度转角指示器对舵面偏角进行实测，将舵面偏角折算为电刷位置，得到舵面偏角误差补偿方法验证曲线，如图9所示。

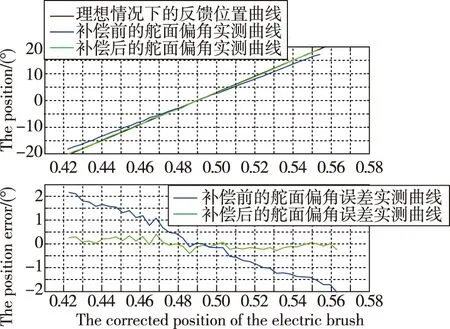
图9 舵面偏角误差补偿方法验证曲线Fig.9 Validation curve of rudder deflection error compensation method

由图9可知：舵面偏角误差得到有效修正，补偿后的舵面偏角实测曲线与理想情况下反馈位置曲线几乎完全重合。在舵面偏角范围±20°内，补偿前，反馈位置误差和舵面偏角呈负相关关系，最大反馈位置误差对应舵面偏角为-20°和+20°，反馈位置误差分别为2.17°和-2.02°；补偿后，反馈位置误差主要来自测量误差，最大反馈位置误差仅为0.38°。

5 结论

本文基于电位器等效电路模型，对电位器基准电压线性误差和负载效应非线性误差展开了机理分析和实验验证，提出了一种舵机电位器的反馈位置误差补偿方法，对AD芯片采集的基准电压和实际反馈位置进行解算，得到了基准电压线性误差补偿系数和负载效应非线性误差补偿系数，实现了舵面偏角的有效修正，并开展了补偿方法的验证工作。实验结果验证了该反馈位置误差补偿方法的正确性和有效性，实现了舵面偏角的有效修正，且成本低，易于工程应用，对提高导弹控制效率具有重要意义。