空间平台机动变轨自主导航研究

胡雨可，严恭敏，郭 鹍

(1.西北工业大学自动化学院，西安 710129；2.中船航海科技有限责任公司，北京 100070)

0 引言

基于现代航天与空间技术基础发展起来的空间机动平台，使现代战争的作战范围延伸到了轨道空间范围内。美国的“轨道快车”计划已于2007年完成全部演示任务，其空间平台具有很强的机动变轨能力[1]；此外，“轨道试验飞行器”计划截止2016年，已先后4次发射X-37B升空，其具有监视及摧毁其他卫星的能力[2]。可见空间平台作为武器发射平台在现代战争中将发挥重要作用，因此提高空间平台的机动能力和自主导航能力具有极大的战略意义。

卫星工具包(Satellite Tool Kit，STK)提供了高精度地球引力势、大气阻力、太阳光压以及各种摄动模型，可对卫星飞行轨迹进行高精度模拟。利用STK设计空间平台在轨飞行的轨迹，或者对在轨飞行段进行惯性/星光组合导航仿真分析，国内外学者已进行了大量研究，取得了显著的成果[3-5]。但在变轨机动过程中，空间平台机动的快速变化，必然使得惯性/星敏感器的组合效果与在轨情况不同，而在这方面的研究还并不多见。

本文主要运用STK仿真了空间平台机动变轨方案；再利用Kalman滤波设计了组合导航方案，将惯性导航能够连续提供输出但长时间误差积累的特点，与星光导航输出频率不高但长时无误差累积的特点进行优势互补[6-9]，有效提高了空间平台的自主导航能力；并采用基于协方差更新的误差分配方法[10-12]，分析了导航过程中影响导航精度的主要因素。

1 惯性/星敏感器的Kalman滤波算法

空间平台一般处于较高轨道，其轨道高度约为200～4000km，甚至更高。在没有大气层影响的情况下，采用大视场星光敏感器(Star Sensor，SS)可以避免小视场星体跟踪器在大机动时无法稳定工作的问题。在此基础上，利用星敏感器输出和惯导输出建立组合导航的状态方程和量测方程。

1.1 系统状态方程

组合导航系统的状态方程可表示为

(1)

在地心惯性坐标系i下，惯导系统的导航微分模型为[13]

(2)

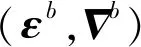
(3)

导航误差可表示为

(4)

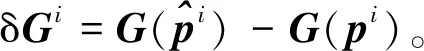
1.2 量测方程

(5)

由式(5)可得

(6)

利用式(6)的反对称结构特性，得到量测方程

(7)

式中，H=[I3×303×12]。

2 组合导航的误差分析

2.1 基于协方差更新的误差分配

误差分配分析的目的是通过仿真手段获得各个误差源在整个空间平台自主导航过程中的影响大小，从而在实际应用前能对现有的器件精度指标进行调整。利用Kalman滤波方程中的协方差矩阵更新公式能够准确得到每个时刻状态向量X中任意一项误差的方差。通过线性误差模型的叠加性可以得到任意一项状态在任一时刻的误差分配清单。对于组合导航系统而言，需要建立真实高阶和实际低阶的两种误差模型。真实高阶模型尽可能地包含各种误差源，而设计的低阶次优滤波器则通过计算的增益K对真实的误差状态产生影响。

影响最终导航精度的因素包括初始状态误差、过程噪声误差和量测噪声误差。这三类误差的传播特性不尽相同。

由于中、高精度组合导航系统误差模型的线性可加性，任一时刻滤波状态第i个元素误差Xi的方差可以写成如下形式[14]

(8)

2.2 组合导航真实环境的误差模型

1)IMU误差模型[14]

(9)

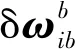
2)重力误差模型

空间平台在变轨机动过程中，由于速度高且变化较快，需要建立合理的重力误差模型来消除重力在导航算法速度更新过程中产生的影响。将重力误差项看作与距离相关的一阶马尔科夫模型

(10)

式中，dδgmdl表示经过无限小的距离ds内重力模型误差的变化量；lg为重力模型的相关距离；ngw为马尔科夫过程的驱动噪声。

对式(10)两边积分得到其时间的模型后，可将重力模型误差写成如下形式

(11)

目前,星敏感器测量精度已经达到角秒级，且误差不随时间累积。因此,本文将星敏感器测量误差考虑为零均值的白噪声过程，其误差模型就不再赘述。

3 基于STK的变轨轨迹生成

3.1 球谐函数重力模型

常用的低阶WGS84重力模型未考虑重力的北向和东向分量，在高于20km的空域，WGS84的重力模值误差将对导航精度产生较大影响。针对空间平台高空域的工作环境，采用高阶的球谐重力模型较为适合。

实际应用中，假设地球质量关于极轴对称分布，地球坐标系原点、地球质心和地球几何中心一致，并且不考虑重力异常影响，那么球谐模型地球引力位可以简化为[15]

(12)

其中，Jn为球谐波系数。此时引力的表达式为

(13)

(14)

由于随着重力模型阶数的增长，重力的计算量会大幅增加，而球谐波系数Jn将会衰减，从而导致重力模型中的高阶项对重力影响较小。综合考虑空间平台工作的高度环境和重力模型计算的复杂程度，STK生成轨迹采用J4重力模型，惯导算法中也使用相同的J4模型进行IMU反演和导航计算。

3.2 机动变轨轨迹生成

利用STK中的高精度卫星轨迹模型(High-Precision Orbit Propagator，HPOP)生成空间平台的轨道数据。通过设定空间平台的6个轨道根数得到飞行轨迹，如图 1所示。导航参数和机动参数可从STK报表功能中获取，将获取的导航参数通过惯导反演算法进行验证，确定STK中的数据是否可用，以及惯导算法是否满足导航需求。

图1 飞行轨迹3D图像Fig.1 3D flight trajectory

此外，借助STK中的Astrogator功能，通过对初始轨道、目标轨道以及3个轴向加速度的设置，可以得到实验所需要的共面变轨或者是非共面变轨轨迹。为了研究变轨机动过程中的导航精度，轨道机动不能用理论研究时所采取的冲量法，应该考虑发动机推力是一个有限量，轨道根数的改变具有一定的时间过程。变轨过程采用轨道机动的制导方法，将STK中Astrogator功能的Maneuver Type改为Finite，通过改变空间平台的加速度实现变轨机动。

4 仿真结果与分析

仿真结果如图2～图10所示，其中图2和图3为在轨段惯性/星敏感器组合导航与惯性导航的三轴姿态与速度误差对比；图4为组合导航的位置误差分配结果；图5和图6为变轨机动过程中惯性/星敏感器姿态组合导航与纯惯导的三轴姿态与速度误差对比；图7～图9为机动变轨过程中加速度计常值偏置分别为100μg和10μg时惯性导航误差对比；图10为变轨机动过程的纯惯导速度误差分配结果。其中图4与图10横坐标含义为：1)初始时刻的导航参数误差；2)陀螺静态零偏误差；3)加速度计静态零偏误差；4)陀螺动态零偏误差；5)加速度计动态零偏误差；6)陀螺随机游走误差；7)加速度计随机游走误差；8)陀螺刻度系数相关误差；9)加速度计刻度系数相关误差；10)不正交与不对准误差；11)重力模型误差；12)量测噪声误差。

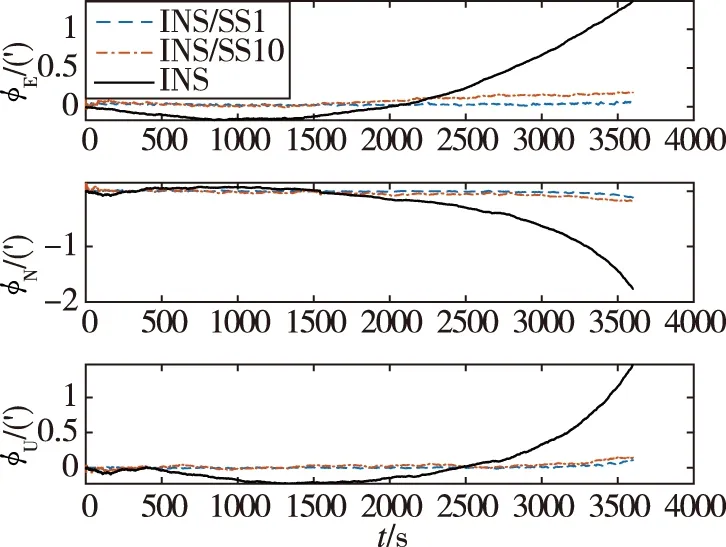
图2 惯性/星敏感器姿态组合与惯导姿态误差对比Fig.2 Attitude error of INS/SS compared with INS

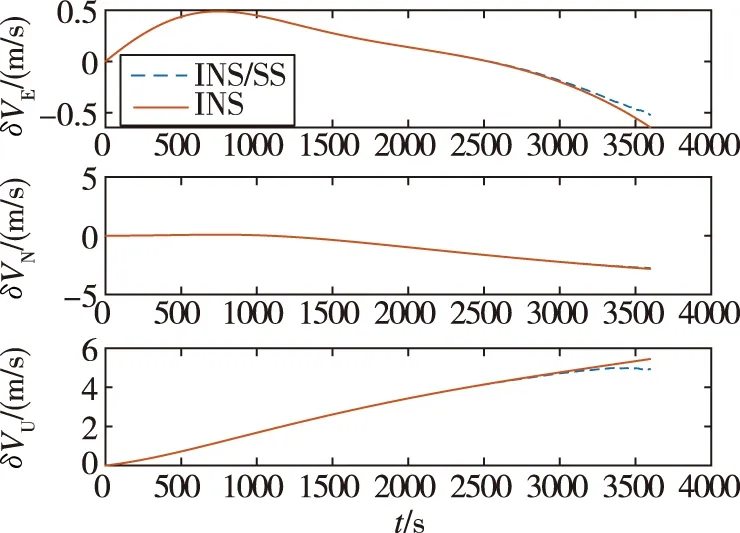
图3 惯性/星敏感器姿态组合与惯导速度误差对比Fig.3 Velocity error of INS/SS compared with INS

图4 组合导航位置误差分配Fig.4 Position error distribution of INS/SS

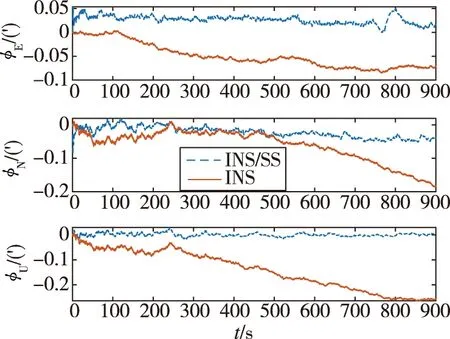
图5 变轨机动段组合导航与惯导姿态误差对比Fig.5 Attitude error of INS/SS compared with INS during orbit maneuvering

图6 变轨机动段组合导航与惯导速度误差对比Fig.6 Velocity error of INS/SS compared with INS during maneuvering

图7 不同加速度计常值偏置姿态误差对比Fig.7 Attitude error comparison with different

图8 不同加速度计常值偏置位置误差对比Fig.8 Position error comparison with different

图9 不同加速度计常值偏置速度误差对比Fig.9 Velocity error comparison with different

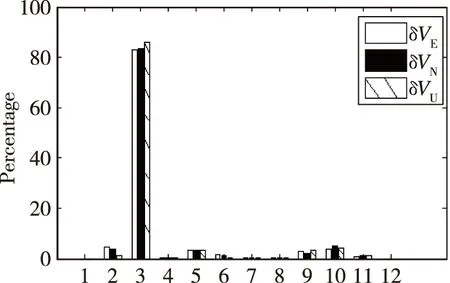
图10 变轨机动段速度误差分配Fig.10 Velocity error distribution during orbit maneuvering

对仿真结果分析如下：

1)如图2和图3所示，在轨段与轨道机动段捷联惯导解算的姿态误差随时间的增加而积累，导航参数发散速度很快。惯性/星敏感器姿态组合导航对姿态误差有明显修正，姿态迅速收敛，稳定误差精度达到5″，有效地抑制了姿态误差的发散。图2中点划线和虚线分别表示星敏感器姿态输出精度为10″和1″时的姿态误差曲线，可见1″精度的星敏感器对姿态的修正效果优于10″。由于太空中在轨段飞行，空间平台几乎处于完全失重状态，其加速度计的输出几乎为0。由速度误差方程

(15)

2)由图4可知，在轨段组合导航中影响位置误差估计的主要因素分别是：不正交与不对准误差、加速度计刻度系数相关误差和重力模型误差。量测噪声误差会对位置精度产生影响，但并不是决定性的因素。

3)图7～图9显示，变轨机动过程中加速度计的精度对姿态影响不明显，但对空间平台速度与位置精度有较大影响，100μg和10μg的加速度计常值偏置仿真位置误差分别约为200m和20m。由此可见，加速度计是影响定位精度的主要因素。而在纯惯导速度误差分配图10中表明，影响定位精度的最主要因素是加速度计静态零偏误差，结论与图8分析一致。

5 结论

本文采用惯性/星敏感器组合，通过STK仿真软件设计了复杂摄动模型，更接近真实环境的高精度空间平台机动变轨轨迹；利用Kalman滤波方法研究了空间平台在变轨机动过程与在轨飞行时的导航精度；最后通过误差分配方法，分析了影响导航精度的主要因素，为提高空间平台自主导航能力提供了依据。

实际应用中，为了提高空间平台的自主导航能力，提出了以下几点建议：1)长航时飞行时，适当提高星敏感器测量精度将有效减小空间平台的姿态误差；2)采用简化球谐J4重力模型能够满足空间平台的导航需求；3)机动变轨时间在20min以内时，无论是组合导航或者纯惯导，采用加速度计常值偏置为10μg甚至更高精度的加速度计将大幅提高空间平台的定位精度，从而实现空间平台机动变轨时的自主导航。