MEMS惯测技术在管道测绘系统中的应用

2019-12-11杨继红吴亮华

导航定位与授时 2019年6期

杨继红，马涛，吴亮华，季阳

(1.海装驻北京地区某军事代表室，北京 100074; 2.北京自动化控制设备研究所，北京 100074)

0 引言

管道作为石油、天然气最经济合理的运输方式，具有诸多优点，但油气管道长期服役后，会因外部干扰、腐蚀、管材和施工质量等原因造成安全隐患。因此，需要借助各种检测技术，有效地检测出管道存在的缺陷和变形，并精准确定存在缺陷和变形的位置，为管道的完整性管理和安全评价提供依据，确保管道的安全运行。

随着惯性技术的不断发展，采用惯性技术进行测绘已经取得了许多成功的案例[1]，其中，采用惯性测量装置精确测绘出管道的地理坐标[2-6]，对管道缺陷进行准确定位，是一种十分有效的方法。并且，随着微机电系统(Micro-Electro-Mechanical System，MEMS)技术的不断成熟，应用MEMS惯测技术可以对口径更小的管道进行测绘，扩大了惯性技术对管道测绘的覆盖范围。

惯性测量技术中利用载体加速度的二次积分获得载体位置，因此，获得积分初始值也是惯性测量装置在工程应用中的重要环节。一般地，管道惯测装置的初始位置由外部装订，初始速度为0，而初始姿态值需要由惯测装置初始对准得到[7]。

由于MEMS惯性器件的测量精度通常较低，MEMS陀螺敏感的地球角速度湮没在陀螺噪声中，无法进行自对准。因此，MEMS惯测装置在使用中经常利用外部信息为其提供方位初始信息，如磁罗盘、双天线卫星接收机等。但由于管道测绘的具体应用条件，难以采用这些设备提供初始方位，造成MEMS惯测装置在管道测绘中使用不便。

本文利用地标点信息，直接为MEMS惯测装置装订方位信息，并利用里程计信息作为观测量，采用因子图原理和和积算法进行组合导航，利用到达路标点的信息修正初始方位。初始方位修正后，再次进行组合导航，并进行平滑计算，实现管道中心线的精确测量，测量现场无需使用其他配套设备，也无需额外操作，有利于MEMS惯测装置在管道测绘中的应用推广。

1 系统模型

1.1 坐标系定义

n：导航坐标系oxnynzn，东北天地理坐标系，xn轴指向东，yn轴指向北，zn轴指向天；

b：惯测装置载体坐标系oxbybzb，右前上坐标系，xb轴指向惯测装置的右侧，yb轴指向惯测装置的前向，zb轴指向惯测装置的上方；

m：里程计载体坐标系oxmymzm，右前上坐标系，ym轴指向里程计测量轴的前向，xm轴与ym轴垂直指向右侧，zm轴与oxmym面垂直指向上；

i：惯性坐标系oxiyizi，与b系初始时刻指向相同；

e：地球坐标系oxeyeze，oxeye平行于赤道平面，xe轴指本初子午线方向，ze轴指向北极，ye轴与其他两轴组成右手系。

1.2 惯性导航误差模型

本文直接给出惯性导航误差模型如下[8-11]

(1)

1.3 系统状态模型

选取系统的状态变量为

其中，βx和βy分别为里程计对应轴向的安装误差，δK为里程计标度因数误差。

假设惯性器件误差为零偏误差与白噪声之和，零偏误差为随机常值；假设里程计安装误差残差及标度因数误差在系统运行中基本保持不变，则

(2)

根据式(1)、式(2)可得系统的状态方程为

(3)

其中：F为系统状态矩阵，W为系统噪声，分别由陀螺测量噪声和加速度级测量噪声组成。

1.4 系统观测模型

里程计输出信息为位移增量，可在一定时间内对其进行累积[12-15]，并且与同时间内的惯性导航位移做差，得到系统的观测变量，即

(4)

根据式(4)得系统的观测方程为

Z=HX+V

(5)

其中：H为观测矩阵，V为观测噪声，ΔS为里程计输出累积的位移变化量。则观测矩阵为

(6)

2 基于因子图的递推估计算法

因子图是一种用来描述如何将多变量的全局函数分解成多个局部函数乘积形式的双向图[16]，由变量节点、函数节点和边线组成。因子图的边线是指变量节点和函数节点的连线，当且仅当该变量是函数的自变量时，对应的变量节点才与对应的函数节点用边线连接。

将式(3)、式(5)表示的线性系统进行离散化，可得

(7)

式(7)表示的系统为一阶马尔科夫系统，画出其因子图如图1所示，其中白色圆圈表示标量节点，黑色方框表示函数节点。

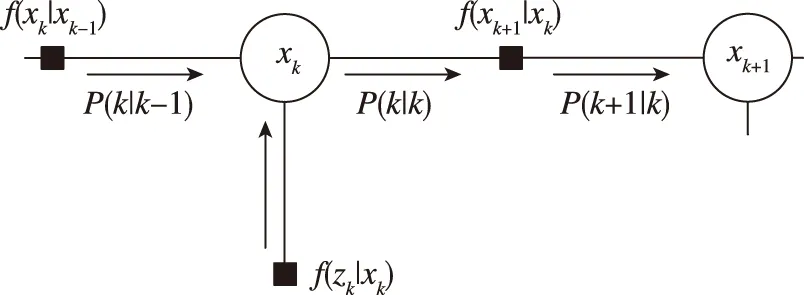
图1 组合导航系统的因子图Fig.1 The factor graph of integrated navigation system measurement

根据因子图的和积算法[17]，由变量节点传递给函数节点的消息表示为

μx→f(x)=∏h∈n(x){f}μf→x(x)

(8)

由函数节点传递给变量节点的消息表示为

μf→x(x)=∑～{x}(f(X)∏z∈n(f){x}μz→f(z))

(9)

根据图1所示的系统因子图，将系统(7)写成条件概率密度函数的形式，可以表示为

f(x1,…,xk|z1,…,zk)=

(10)

将变量节点传递给函数节点的消息表示为P(k|k)，将函数节点传递给变量节点的消息表示为P(k+1|k)，则根据图1和式(8)、式(9)可得

P(k|k)=f(xk|z1,…,zk)

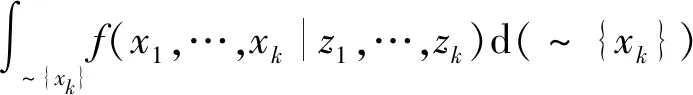
=P(k|k-1)f(zk|xk)

(11)

(12)

根据式(11)和式(12)，即可实现对系统状态变量的递推估计。

3 试验结果

为了验证MEMS惯测技术在管道测绘系统中的应用效果，进行了管道牵引试验，试验设备连接如图2所示。试验管道长度约103.8m，牵引速度约为1m/s，共试验3次，第2次和第3次试验在管道中部约50.5m处，较第1次试验分别沉降20cm和41.5cm，共采集3个条次数据，管道中心线测绘结果如图3～图5所示。

图2 牵引试验设备连接示意图Fig.2 Schematics of device linking in dragging tests

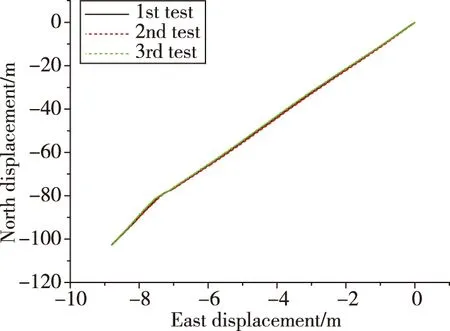
图3 牵引测试水平位移结果Fig.3 Horizontal displacement in dragging tests

图4 牵引测试北向误差结果Fig.4 North displacement error in dragging tests

图5 牵引测试高度结果Fig.5 Height in dragging tests

由于测试没有绝对基准，需要通过3次测量的重复性来说明测量结果精度，所以将3次试验的同项结果在同一曲线图中呈现。图3和图4分别为3次试验的水平位置测量结果和高度测量结果，可以看出，3次测试的水平位移基本相同，但由于每次试验的时间长度略有不同，无法通过直接相减观察位移测量结果的重复性。因为实际管道在北向位移随里程基本呈线性变化，所以利用各次试验的北向位移结果直接与随里程线性的直线相减作为北向位移测量误差，结果见图4。可以看出，各次试验的北向位移基本相同，最大相差点在管道中部沉降点之后，为第1次试验和第3次试验的差值，约为5cm。图5为高度测量结果，可以看出测量结果基本体现了试验中的沉降过程，在沉降点的测量结果分别为6.55m、6.33m和6.18m，最大偏差同样在5cm以内。