GGA+U方法研究不同浓度镧(La)与氮(N)掺杂纤锌矿ZnO的光学性质
2019-12-09刘桂安王少霞赵旭才雷博程黄以能张丽丽
刘桂安,王少霞,赵旭才,雷博程,夏 桐,黄以能,2,张丽丽,2
(1.伊犁师范学院 物理科学与技术分院 新疆凝聚态相变与微结构实验室,伊宁 835000; 2.南京大学 物理学院 国家固体微结构重点实验室,南京 210093)
1 引 言
ZnO是一种宽禁带半导体材料,禁带宽度为3.37 eV,激子束缚能高达60 meV,具有高的化学稳定性以及优良的压电特性,使其在电学、光学以及电磁学等方面具有很大的应用潜力[1-3]. 自从1997 年Tang 等[4]报道了ZnO 薄膜的近紫外受激发射现象以后,ZnO再次成为当今半导体材料研究领域的热点. 近年来,人们对ZnO材料做了大量的实验与理论方面的研究工作,并且还发现通过掺杂可以改变ZnO 的性质. 例如:Minami 等[5]人发现了Sc和Y掺杂的ZnO 体系的导电性显著增强;对其掺杂Al,Gs和In等元素可得到导电性能较好的n型ZnO薄膜材料[6-9];Cr,Cd,Cu[10-12]等金属掺杂ZnO后,在可见光区域光催化活性增强;研究发现N,S,C等非金属掺杂的ZnO也出现了可见光区域光吸收增强的现象[13-15],然而,金属掺杂和非金属掺杂都存在一定的不足,比如金属掺杂容易形成金属团簇,使得体系出现不稳定相,而非金属掺杂中,由于其溶解度低、电离能高等原因,很难实现ZnO的非金属掺杂[16],所以人们想到用共掺的方式来对其改性. Hou等人[17]发现在Al-2N共掺的ZnO会发生光学吸收谱吸收边红移的现象;而对于La-N共掺杂的研究方面,齐蕾[18]等人发现La-N共掺杂TiO2光催化剂与单掺N的TiO2以及纯TiO2相比,光催化活性有明显提高,当煅烧温度为600 ℃,添加La的摩尔分数为0.10%时,光催化活性最佳. 鉴于以上原因本文将利用第一性原理方法,以纤锌矿ZnO为本征体,将不同浓度镧(La)与氮(N)共掺杂入纤锌矿ZnO中,计算得到本征ZnO及掺杂体系的电子结构及光学性质,并进行研究对比,得出相关结论,从而为ZnO材料的掺杂,改善其电学性质、光学性质提供理论依据.
2 计算方法及模型
本实验的计算工作是基于密度泛函理论的第一性原理方法[19, 20],利用Materials studio 8.0中的CASTEP软件完成计算. 具有六角纤锌矿结构的ZnO 属于六方晶系,空间群为P63MC.晶格常数实验值为[21-23]:a=b= 0.325 0 nm ,c= 0.5207 nm ,c/a=1.602,α=β=90°,γ=120°在计算中不考虑自旋影响,选用超软赝势来近似描述价电子与离子之间的相互作用;平面波截断能Ecut为300 eV,布里渊区K点取值为2×2×2,自洽精度(SCF)为2.0×10-6eV/atom,交换关联函数用GGA/PBE进行处理;并采用GGA+U的方法来修正带隙[24],当采用GGA+U(UZn:3d=8.12 eV、UO:2p=4.64 eV)得到其禁带宽度为3.374 eV,与实验值符合的非常好. 3D模型中各原子的位置分别为:Zn原子在立方体的面心,其坐标为(0.330,0.6667,0),O原子在立方体的体心,其坐标为(0.3330,0.6667,0.3828). 以2×2×1的ZnO超胞作为计算不同掺杂浓度对电子结构影响的模型,具体为非金属元素N原子替代模型内部的一个O原子,形成ZnO0.875N0.125超胞模型;用金属原子La原子代替一个Zn原子,形成Zn0.875La0.125O再用不同浓度元素La替代ZnO0.875N0.125模型中的Zn原子,形成Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)的超胞模型,其中本文所涉及的4种原子的电子组态分别为:Zn(3d104s2),O(2s22p4),La(5d16s2),N(2s22p3),掺杂体系结构如图1所示.
3 计算结果与讨论
3.1 结构优化
表一为本征ZnO经过几何优化过的晶格参数,由表中数据可得,本实验得出的计算值与袁俊辉得出的计算结果相近. 与实验值与实验值相比,本实验ZnO的晶格常数和体积的误差都在百分之一以内,在计算误差的合理可接受范围之内,即说明本文所选计算参数是合理的.
表1 本征ZnO晶格常数和体积
Table 1 the lattice constants and volumes of pure ZnO
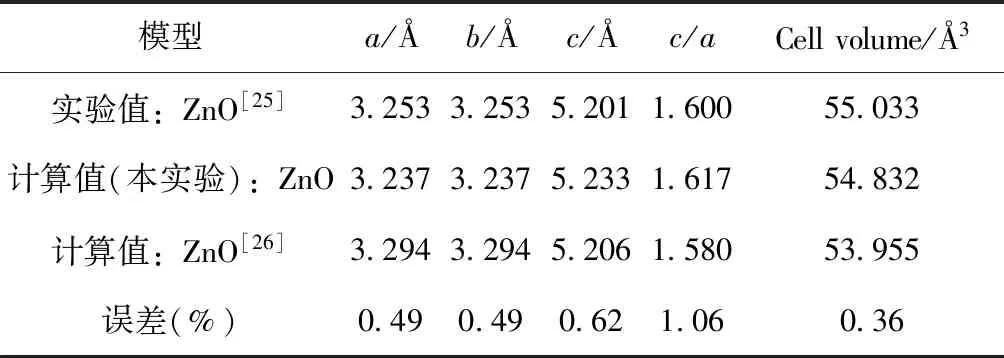
模型a/Åb/Åc/Åc/aCellvolume/Å3实验值:ZnO[25]3.2533.2535.2011.60055.033计算值(本实验):ZnO3.2373.2375.2331.61754.832计算值:ZnO[26]3.2943.2945.2061.58053.955误差(%)0.490.490.621.060.36
表二为ZnO及La、N单掺和共掺体系晶格常数和体积,由表中数据可得单掺体系的晶格常数和体积相对于本征ZnO体系都有所增加,这可能是由于引入的杂质La、N的半径都比被替代原子Zn、O的半径要大,所以导致单掺体系发生如此变化. 在共掺体系中随着La浓度的增加,体系的晶格常数以及体积都呈现增大的趋势,但c/a的值却在逐渐变小,这说明随着La浓度的增加,晶格畸变的程度也在增大,对晶格周期势场的影响也就越大,这将在后面的电子结构分析中体现出来.

图1 结构模型 (a). 纯ZnO (b). ZnO0.875N0.125; (c). Zn0.875La0.125O;(d). Zn0.875La0.125O0.875N0.125; (e). Zn0.75La0.25O0.875N0.125; (f). Zn0.625La0.375O0.875N0.125Fig. 1 Structural models a). Pure ZnO; b). ZnO0.875N0.125; c). Zn0.875La0.125O; d). Zn0.875La0.125O0.875N0.125; e). Zn0.75La0.25O0.875N0.125 f).Zn0.625La0.375O0.875N0.125
表2 ZnO及La、N单掺和共掺体系晶格常数和体积
Table 2 Lattice constants and volumes of ZnO and La, N single doping and co-doping systems
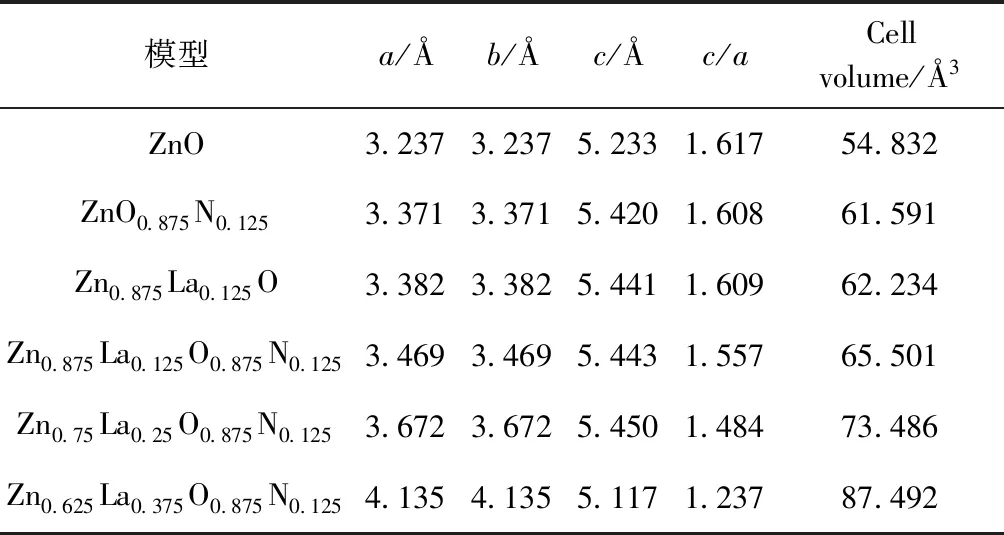
模型a/Åb/Åc/Åc/aCellvolume/Å3ZnO3.2373.2375.2331.61754.832ZnO0.875N0.1253.3713.3715.4201.60861.591Zn0.875La0.125O3.3823.3825.4411.60962.234Zn0.875La0.125O0.875N0.1253.4693.4695.4431.55765.501Zn0.75La0.25O0.875N0.1253.6723.6725.4501.48473.486Zn0.625La0.375O0.875N0.1254.1354.1355.1171.23787.492
表3为纯ZnO、单掺La、N体系及Zn1-xLaxO0.875N0.125(x=0.125,0.25,0.375)共掺体系几何优化后体系的总能量,形成能以及键布局. 形成能表示掺杂形成的难易程度,其值越正,表示不容易形成,其值越负,表示杂质越容易掺杂进入,其公式如下:
Ef=Edefect-Eperfect-nEN-mELa+nEO+mEZn
(1)
公式中Eperfect和Edefect分别掺杂前后体系总能量,EN、ELa、EO、EZn分别为N、La、O、Zn原子的基态能量. n,m分别表示掺入的杂质原子的个数和被替代原子的个数. 从表中可以看出,单掺La、N体系以及Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体相比较于纯ZnO,体系总能量增大,其形成能有所减小,其中Zn0.75La0.25O0.875N0.125体系的形成能最小,说明该体系最为稳定. 键布居数为正,数值越大其共价性越强,若其值为负,数值越小其离子性越强. 由表中键布局数可知:从单掺到共掺随着共掺体系La浓度的增加,最大及最小Zn-O键长的差值在减小,证明共掺体系发生了较强的畸变,并且随着掺杂浓度的升高,其畸变的强度就越强,此结果与晶格常数分析结果一致,该现象会导致ZnO原有的晶体对称性被破坏,正负电荷中心不在重合,而产生局域电势差,有利于阻碍光生空穴和电子对的复合,进而有望提高材料的光催化性能. 且各掺杂体系的La-O键布局数比Zn-O键布局小,说明La-O的共价性比Zn-O差,当本征ZnO体系引入La杂质后体系的稳定性变差,而Zn-N键布局数比Zn-O键布局大,Zn-N共价性较强,说明N的掺入可改善因La掺入的不稳定性.
3.2 电子结构分析
图2(a)是纯ZnO的能带结构图,经计算得,纯ZnO的禁带宽度是3.374 eV,与实验值3.37 eV符合的很好,说明计算得到的能带变化规律是可信的,可以对能带和态密度进行定性分析.
对比图2(b)为N单掺ZnO能带图,其禁带宽度变为3.77 eV,相比较于纯的ZnO略微的增大,但由于N的掺杂引了杂质能级,其与价带和导带的间隙分别是0.55 eV、1.30 eV,可作为电子从价带跃迁到导带的桥梁,即电子可以先被很小的能量激发跃迁到杂质能级,在继续吸收能量从杂质能级跃迁到导带,所以外界只需要提供很小的能量就可以使电子从价带跃迁到导带,从而实现ZnO对可见光的吸收,提高其对光的利用率. 其吸收带边也会发生红移,后面得到的吸收图谱一致.

表3 各模型的能量,形成能,键布居数,与键长
a为各体系中最长Zn-O键的布局数,b为各体系中最短Zn-O键的布局数,c为各体系中最长La-O键的布局数,d为各体系中最短La-O键的布局数,e为各体系中最长 Zn-N键的布局数.
对比图2(c)为La单掺ZnO能带图,与图(a)对比可知其其导带和价带都有略微的下移使禁带宽度减小了0.004 eV,这有利于吸收带边的红移. 图(d-f)为Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系的能带图,其禁带宽度分别为4.22 eV、3.36 eV、4.98 eV,虽然三种共掺体系的禁带宽度都有略微的增大,但共掺体系产生了杂质能级,且体系杂质能级与价带和导带之间的间隙为分别为1.58 eV、1.41 eV;1.33 eV、1.60 eV;0.82 eV、0.95 eV,相比较其原来的禁带宽度是减小的,而且其杂质能级的产生会阻碍电子和空穴的复合,提高其光催化活性.
比较Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系的能带图三张共掺体系能带图,随着掺杂La浓度增加,杂质能级与价带和导带的间隙逐渐减小,电子跃迁所需能量逐渐减小,其中Zn0.625La0.375O0.875N0.125的间隙最小,电子发生跃迁所需能量最小,说明其光催能力最强.
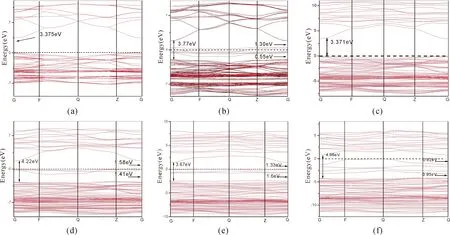
图2 能带图 (a).纯ZnO (b).ZnO0.875N0.125;(c).Zn0.875La0.125O; (d). Zn0.875La0.125O0.875N0.125; (e). Zn0.75La0.25O0.875N0.125; (f). Zn0.625La0.375O0.875N0.125Fig.2 Band structures: a). Pure ZnO; b). ZnO0.875N0.125; c). Zn0.875La0.125O; d). Zn0.875La0.125O0.875N0.125; e). Zn0.75La0.25O0.875N0.125 f). Zn0.625La0.375O0.875N0.125
从图3(a)的态密度图看出,未掺杂时,在费米能级附近,纯ZnO的价带主要是由Zn-3d态和O-2p态贡献,Zn-3d态和O-2p态相互叠加形成-3.40 eV处的态密度峰,O的2p态引起了-1.17 eV的态密度峰,导带中最高峰受Zn-3d的影响.
由图3(b)的态密度图看出,N单掺杂体系,价带主要是由Zn-3d态、O-2p态贡献、N-2p态贡献. 并且禁带中间出现了一个态密度峰,这说明图2(b)中杂质能级的出现由N-2p态做主要贡献.
由图3(c)的态密度图看出,La单掺杂体系,价带主要由Zn-3d态、O-2p态贡献贡献,导带主要由La-5d态贡献.
由图3(d-f)的态密度图看出,在Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)三个共掺体系中,费米能级附近主价带要分别由Zn-3d态、O-2p态和N-2p态贡献,导带主要由La-5d态贡献. 并且在禁带形成的杂质能级大部分由N-2p态贡献,只有少部分由La-5d态贡献.
由于杂质能级的产生,掺杂体系相比于纯ZnO,其导电性能都有所增强,同时也使其光催化功能有所提升.
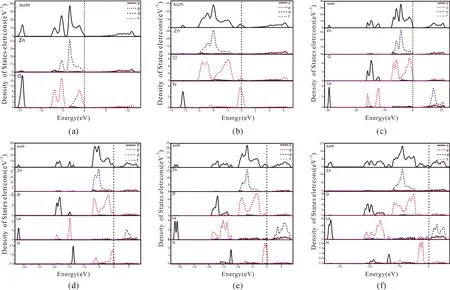
图3 能态密度图 (a).纯ZnO (b).ZnO0.875N0.125;(c).Zn0.875La0.125O; (d).Zn0.875La0.125O0.875N0.125; (e).Zn0.75La0.25O0.875N0.125; (f).Zn0.625La0.375O0.875N0.125Fig. 3 Densities of states a).Pure ZnO; b).ZnO0.875N0.125; c).Zn0.875La0.125O; d).Zn0.875La0.125O0.875N0.125; e).Zn0.75La0.25O0.875N0.125 f).Zn0.625La0.375O0.875N0.125
3.3 光学性质
众所周知,介电函数可以反映固体能带结构以及各种光谱信息,是沟通固体电子结构和带间跃迁微观物理过程的桥梁.
图4是纯ZnO体系,La、N单掺体系和Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系的介电函数实部图. 从图中我们可以看到:五种体系的静介电常数分别为1.83、6.40、6.12、2.57、6.87、11.56,可以看出单掺N体系的静介电常数大于纯ZnO体系的,而在Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)三个共掺体系中,随着镧浓度的增加,静介电常数逐渐增大,经对比可得单掺La、N体系和Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)三种共掺杂体系静介电常数比纯的ZnO的静介电常数有所增大,这种变化告诉我们,掺杂是改变物体介电性能的有效手段.
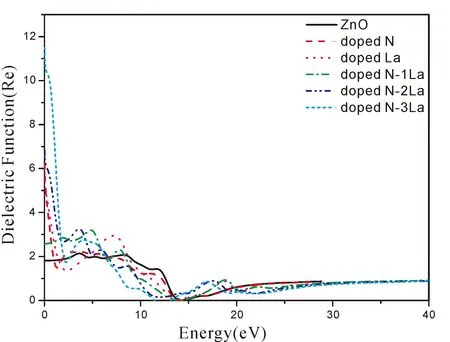
图4 介电函数实部Fig.4 Dielectric function real parts
图5为纯ZnO体系La、N单掺ZnO体系和Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系的介电函数虚部图,从图中我们可以看到:ZnO的介电函数虚部有三个主峰,分别出现在4.61 eV,6.04 eV,15.92 eV处. 4.61 eV处的峰主要由Zn-3d态和O-2p态之间的电子跃迁形成. 单掺N体系的介电函数的虚部有三个主峰,分别出现在0.48 eV,3.71 eV,9.86 eV处. 0.48 eV处的峰主要由Zn-3d态、O-2p态以及N-2p态之间的电子跃迁形成. Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系的介电函数的虚部的主峰,主要由La-5d态、Zn-3d态、O-2p态以及N-2p态之间的电子跃迁形成. 且掺杂后体系的介电函数发生了明显的红移,纯ZnO介电函数值在小于3.5 eV基本为零,而在各个掺杂体系在0-2.5 eV之间都出现了大小不等的峰值,其中Zn0.625La0.375O0.875N0.125的峰值最大,这是因为在图2(f)中可以看到其杂质能级与价带的间隙非常小,这降低了电子跃迁所需要的能量,增大了电子跃迁的概率,此峰就源于杂质能级上的电子到导带的跃迁.
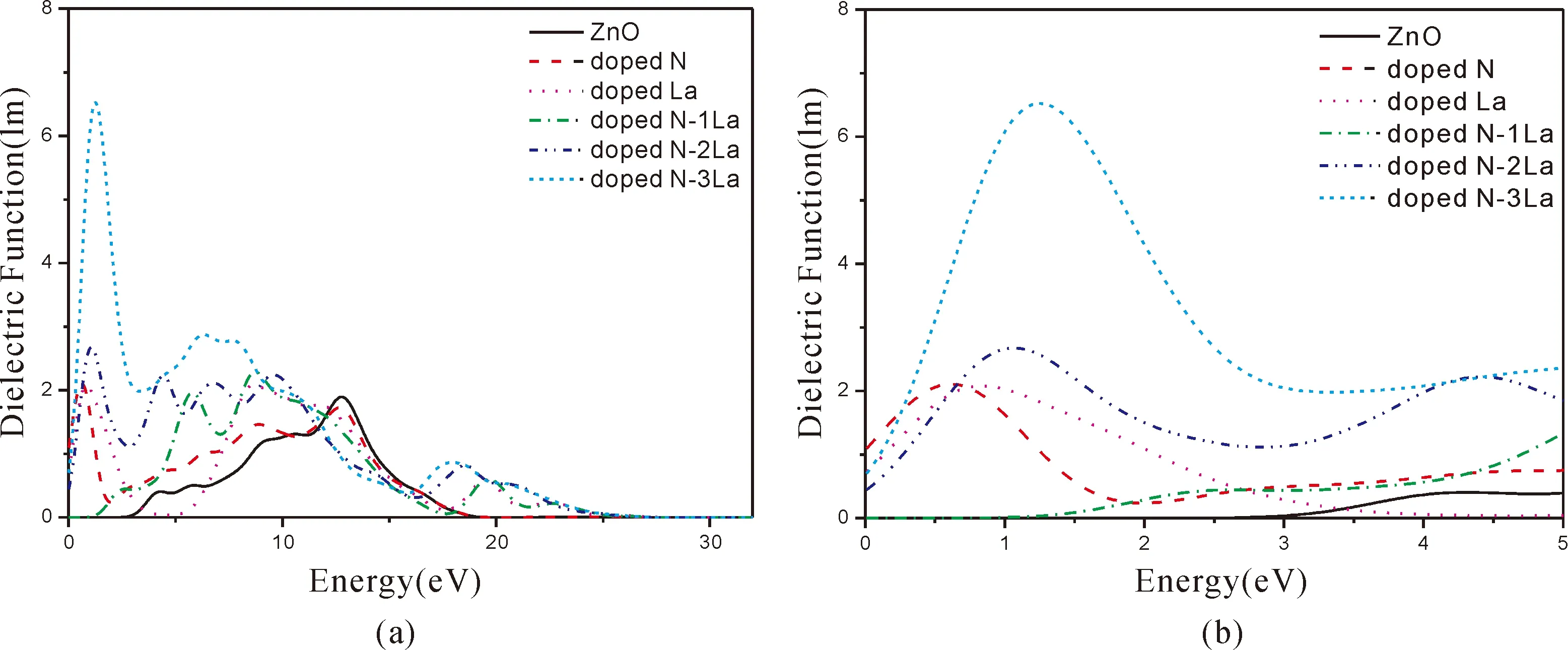
图5 (a). 介电函数虚部 ; (b). 部分放大介电函数虚部Fig. 5 (a). The virtual parts of the dielectric function; (b). The enlarger virtual parts of the dielectric functions
从图6掺杂前后纤锌矿ZnO的吸收光谱可知:相比较纯ZnO,所有掺杂体系的吸收带边都都有发生了明显红移,这得益于杂质能级的引入. 且纯ZnO体系,单掺La、N体系以及Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)的第一个吸收峰的峰分别位于4.30 eV、1.04 eV、1.87 eV、2.51 eV、1.56 eV、2.02 eV. 其中峰值最高的为Zn0.625La0.375O0.875N0.125体系,说明该体系对光的吸收强度最大. 由各体系的第一个峰的位置发现掺杂已经将ZnO对光的吸收范围拓展到了可见光区域1.64~3.19 eV(对应波长为390~770 nm),而且Zn0.625La0.375O0.875N0.125体系不管是吸收范围还是吸收强度都远优于其他体系,这可能是由于其杂质能级与价带的间隙非常小,降低了禁带宽度且提高光生在载流子的效率.
4 结 论
本文主要应用基于密度泛函的第一性原理计算纯非金属元素N掺杂ZnO,La、N单掺ZnO体系以及Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)三个共掺体系,2×2×1超胞体系的能带结构、态密度和光学性质,然后和纯ZnO进行对比.
由晶体结构分析得:纯ZnO、单掺N体系及Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体系几何优化后体系的总能量,形成能以及键布局. 从表中可以看出,单掺N体系以及Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)共掺体相比较于纯ZnO,体系总能量增大,其形成能有所减小,其中Zn0.75La0.25O0.875N0.125体系的形成能最小,说明该体系最为稳定. 随着掺杂浓度的升高,其畸变的强度就越强,该现象会导致ZnO原有的晶体对称性被破坏,有利于阻碍光生空穴和电子对的复合,进而有望提高材料的光催化性能,且由键布局数可知,且N的掺入可改善因La掺入的不稳定性.
由电子结构分析得:相比于纯ZnO体系,单掺La、N体系和Zn1-nLanO0.875N0.125(n=0.125,0.25,0.375)三个共掺体系的禁带宽度都有略微的增加,但是由于掺杂引入了杂质能级使得电子从价带跃迁到导带需要的能量变小,更易发生跃迁,即对低能光的响应更好. 随着La浓度的增加,杂质能级与价带和导带的间隙逐渐减小,电子跃迁所需能量逐渐减小,其中Zn0.625La0.375O0.875N0.125的间隙最小,电子发生跃迁所需能量最小,可以预测其光催能力最强.

图6 (a).吸收光谱; (b).部分放大吸收光谱Fig. 6 (a).Absorption spectra ; (b).Enlarge absorption spectra
由光学性质分析得:与纯ZnO相比,所有掺杂体系吸收带边都发生了红移,表示掺杂后体系对可见光的响应更好了. 其中Zn0.625La0.375O0.875N0.125体系对无论是吸收范围还是吸收强度都是表现最好的,与电子结构的分析相对应.
