井孔散射波数值模拟及提取方法

2019-12-09雷豁黑创罗明璋李修权长江大学电子信息学院湖北荆州434023

长江大学学报(自科版) 2019年12期

雷豁，黑创，罗明璋，李修权 (长江大学电子信息学院，湖北荆州 434023)

肖张波 (中海石油(中国)有限公司深圳分公司，广东深圳 518067)

在早期的地震勘探中，地球被认为是由一系列具有不同弹性的水平层组成，没有考虑各种尺度的非均匀性。而在实际地震勘探中，地层往往具有非均匀性[1,2]，地震波遇到非均匀体会产生散射效应，散射波为量化估计随机非均匀性的强度提供了有用的工具[3～5]，通过散射波场的特征还可以推测非均匀体的分布和性质[6]。现阶段关于地球物理问题的弹性波散射研究主要集中在大尺度传播的地震波方面[7～10]，而关于井孔声波中的弹性散射研究较少。散射波通常被认为是噪声并在数据处理中被抑制，事实上，散射波包含了有关井孔周围岩层非均匀性的重要信息。Tang等[11]研究了二维随机介质的波场响应，结果表明，在单极和偶极波形中都会产生显著的散射波，且偶极子散射主要以S-S(横波-横波)散射为主，可有效用于诊断岩石非均质性。散射波的衰减特性可以用来评价地层的非均匀性以及致密储层的压裂效果[12]，且散射波还可以用来识别地震流体[13]。随着测井技术的发展，包括单极、偶极和多极子的阵列声波测井已经得到广泛应用[14,15]，若能对声波测井数据中的散射波进行提取和适当分析，将为地层的表征提供有价值的信息，为声波测井的处理和解释开辟新的应用前景。为此，笔者数值模拟了各向同性随机介质模型下的波场特征，对单点和井段波形进行了频率-波数(F-K)分析，并利用F-K滤波提取了井孔散射波。

1 各向同性随机介质模型

实际地层中的岩石物性参数在空间分布上往往是非均匀的，既有纵向上的非均匀性，又有横向上的非均匀性，随机介质模型被广泛用于描述岩石中的非均匀起伏变化。随机分布可以用高斯函数、指数函数和Von-Karman函数来描述[16,17]。指数函数、高斯函数表示相关距离上的平滑变化，而Von-Karman函数可以模拟小于相关距离的变化。因此，研究使用Von-Karman函数来模拟岩石的非均匀性。

二维Von-Karman函数表达式为：

(1)

式中：R为Von-Karman函数；x、y分别为横向、纵向位置，m；ε为随机介质的扰动量，1；κ为赫斯特数，1；Г(κ)为伽马函数；a、b分别为X、Y坐标方向的相关距离，m；kκ为第二类κ阶贝塞尔函数。

根据Von-Karman函数，建立了服从随机分布的各向同性随机介质模型，具体模型参数见表1，模型如图1所示。图2给出了距井外1m处的横波速度沿井轴的统计直方图，可以看出，距井外1m处的横波速度围绕背景介质地层横波速度扰动，呈正态分布，反映了地层介质参数空间分布的非均匀性。

表1 各向同性随机介质模型参数

注：r、z分别为径向、轴向距离。图1 各向同性随机介质模型图2 横波速度统计直方图

2 正演模拟

电缆声波测井主要有单极子和偶极子2种类型的声源，由于单极子声波测井的散射波成分比较复杂，不利于散射波的分析，而偶极子声源井外辐射能量主要以SH波(水平偏振横波)为主，散射波以S-S散射波为主，形态单一，故研究以偶极声源辐射的横波和散射波作为研究对象。地层中SH波的位移矢量uSH可以表示为：

(2)

SH波的位移势函数χ表示为：

(3)

根据动力学声波平衡方程，在不考虑外部体积力的情况下，弹性介质在X、Z方向上的位移运动方程可以表示为：

(4)

式中：ρ为弹性介质的密度，kg/m3；ux、uz分别为X、Z坐标方向上的位移，m；t为时间，s；λ、μ为弹性介质的拉梅系数，1。

使用中心差分格式方法，将上述方程离散化，得到二维弹性波动方程的有限差分形式：

(5)

模拟选用的声源类型为瑞克子波，计算时选取声源的中心频率为3kHz，网格大小为0.02m，时间步长为10-6s。

图3为随机介质模型下的SH波在5.8ms时刻的声场快照，可以看到声波在随机介质模型下产生了较为明显的散射波。图4给出了源距为3m，接收间距为0.1524m的井孔阵列波形，理论计算中均匀地层的波形只有直达波成分，通过与相同参数的均匀地层计算结果进行对比，选取均匀介质模型下直达波的时窗(1.5～4.5ms)设定为随机介质模型下直达波的时窗，滞后于直达波时窗的波视为尾波。从图4中可以看到在直达波之后依然出现了较强的尾波，从尾波在阵列波形中相位分布的随机性可以看出，其主要来自于井外地层中的散射。

图3 随机介质模型下5.8ms时刻的声场快照图4 随机介质模型下的井孔阵列波形

图5给出了随机介质模型下直达波和尾波的F-K分析结果，可以看出，随机介质模型下的直达波以地层横波速度(2300m/s)传播，而尾波却以较大的速度(视速度比地层横波速度大)传播，表明其主要来自井外地层的散射。

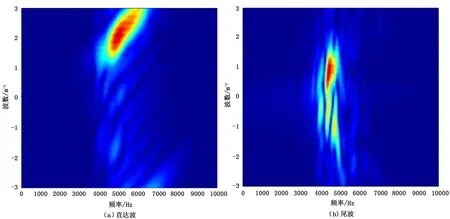
图5 随机介质模型下阵列波形F-K分析

图6(a)为随机介质模型下井段全波数据F-K分析结果，可以看出，在F-K谱中波数分布范围较大，能量主要集中在波数趋近于0的部分；图6(b)、(c)分别为直达波和尾波的F-K分析结果，可以看出，井段直达波能量较强，主要集中在波数趋近于0的区域，尾波能量较弱，波数分布范围较广。

图6 随机介质模型下井段声波数据F-K分析

基于上述特征分析，通过开窗，将图6(a)中波数趋近于0的部分赋值为0，利用二维反傅里叶变换，获取F-K滤波后的井段尾波数据。通过处理前、后的井段波形变密度显示结果(见图7)可以看出，处理后的井段波形滤除了直达波成分，只保留了尾波成分，达到了预期效果。

3 应用

图8(a)给出了某井处理前的井段波形变密度图，可以看出，不仅直达波能量较强，而且在深度3950～3956m、3967～3975m处存在明显的水平地层界面反射波(图中红色箭头标识处)，该种波的存在会严重干扰散射波的提取；利用二维傅里叶变换将现场波形变换到F-K域，将直达波和地层界面反射波信息剔除，然后再利用二维傅里叶反变换将F-K谱变换到时间-深度域；从变换后的波形变密度结果(见图8(b))可以看出，直达波和水平地层界面反射波已经被滤掉，只保留了地层散射波成分，说明F-K滤波方法是有效的。