基于有限元法的大坝应力、变形及稳定分析
2019-12-09艾子欣陈海霞郭穗丰
艾子欣,陈海霞,郭穗丰
(湖南省常德市水利水电勘测设计院,湖南 常德 415000)
实体混凝土重力坝是水利工程常见的挡水建筑物,主要利用自身重力维持坝身的稳定。通常采用刚体极限平衡法来进行抗滑稳定分析,但此法无法反应坝体及坝基不同部位的应力分布和变位场。有限元法(FEA)起始于20世纪中叶,经过70年的不断研究发展,并通过ANSYS、ADINA、MARK、ABQUS等众多通用和专用有限元软件的研发和应用,加之CAD软件与有限元的无缝集成[1- 2],使得有限单元法在工程界得到了广泛的应用[3]。有限元已成为解决边界条件、结构的位移场和应力场等复杂的工程分析计算问题的主要方法,为合理分析重力坝的应力、变形及抗滑稳定分析提供了有效的途径。
目前,采用有限元进行坝体稳定性大多数文献[4- 5]侧重于应力及变形分析,而未根据成果计算其抗滑稳定系数。仅部分文献[6- 8]通过“基于强度储备系数法”“有界降强分项系数法”研究可求得抗滑稳定系数,但相当繁琐。本文寻求一种计算简单、便于应用的潜在滑动面抗滑稳定安全系数计算方法,基于有限元法分析后的坝体平面应力成果,代入调整后抗滑稳定系数公式求出稳定系数。文中以非溢流坝段为例,采用有限单元法计算应力、变形、抗滑稳定系数,综合评定其稳定性。
1 计算方法
1.1 有限元计算原理
本文采用弹性有限元法解决边界条件、结构的位移场和应力场比较复杂的平面问题,其基本理论-弹性理论数值解法的基本概念和步骤[9]如下。
(1) 将结构离散化,划分为大量的、范围有限的单元,采用位移函数法,公式如下:
(1)
式中,u—单元结点的水平位移;v—单元结点的垂直位移;{δ}e—单元结点的位移列向量;[N]—形状函数矩阵,是坐标x,y的函数。
(2) 假定是小变形问题,因此弹性理论中的几何方程依然适用,即:
(2)
并得出单元应变和结点位移的关系式
{ε}=[B]{δ}e
(3)
式中,[B]—几何矩阵。
(3) 根据弹性理论中的广义虎克定律,可以得出单元的应力与应变的关系式 ,即
(4)
式中,{σ}—应力矩阵,[D]—弹性矩阵。
(4) 根据能量原理可以解出单元结点力与结点

表1 水位及泥沙压力基本参数表

表2 重力坝材料物理力学参数表
位移的关系式,即
{F}e=[k]e{δ}e
(5)
式中,[k]e—单元刚度矩阵,{δ}e—单元结点力列向量,{F}e—单元结点作用力。
(5) 列出全部结点的平衡条件,便得出总体平衡方程组,即
[K]{δ}={P}
(6)
式中,[K]—总体刚度矩阵,由单元矩阵组合而成,是一个稀疏的正定对称矩阵;{δ}—全部结点的位移列向量;{P}—全部结点的荷载列向量。
(6) 将几何约束方程引入方程(6),消去总体刚性位移,矩阵求逆便可解出结点位移,即
{δ}=[K]-1{P}
(7)
再利用式(3)和式(4)计算单元应力。
1.2 抗滑稳定计算公式
混凝土重力坝抗滑稳定安全系数是分析其稳定的重要指标。混凝土重力坝设计规范抗剪断公式[10]采用的是刚体极限平衡法。本次以抗剪断公式为基础,将有限元计算出的滑动面各单元σni和τni,代替原公式中的作用于坝体上部结构的滑动平面法向分值∑W和滑动平面切向分值∑P,从而将抗滑稳定系数计算公式[11]调整如下:
(8)
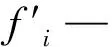
2 工程案例分析
2.1 工程概况
某水利枢纽工程水库总库容9.99亿m3,属于Ⅱ等工程,主要建筑物为2级,次要建筑物为3级。洪水标准采用100年一遇的洪水标准,1000年一遇的洪水标准校核。非溢流坝段采用混凝土重力坝形式,坝顶高程350.82m(扣除防浪墙1.2m后),坝基高程为303.00m,最大坝高47.82m。主要基本参数见表1—2,断面如图1所示。
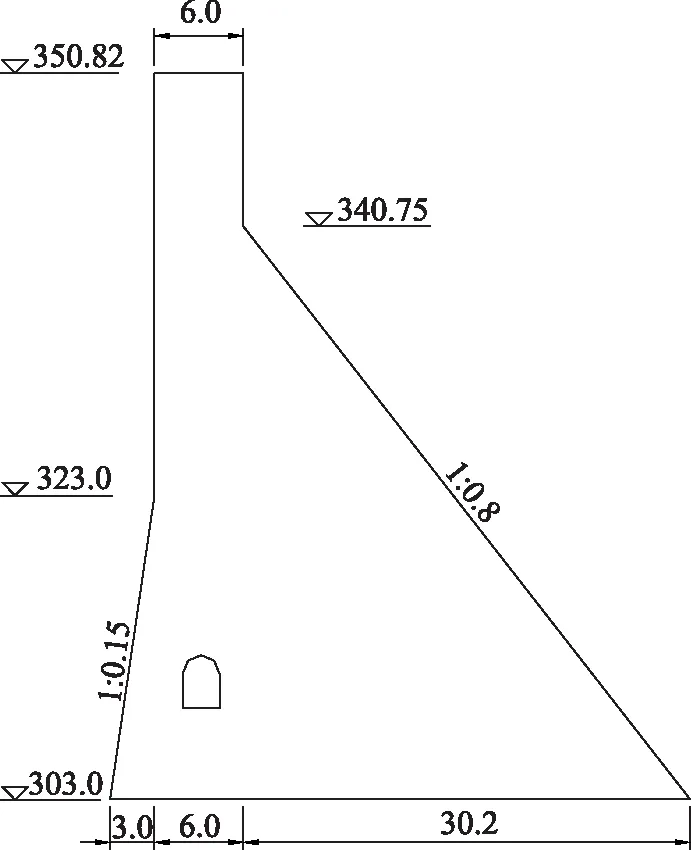
图1 非溢流坝段断面图(单位:m)
2.2 有限单元模型建立
模型建立时,对坝址区的复杂地质条件进行合理概化;输入边界、水位点、扬压力折减处的点等关键点;侧边的约束条件可取水平位移u=0,垂直位移v自由,底边为u=v=0。如图2所示。
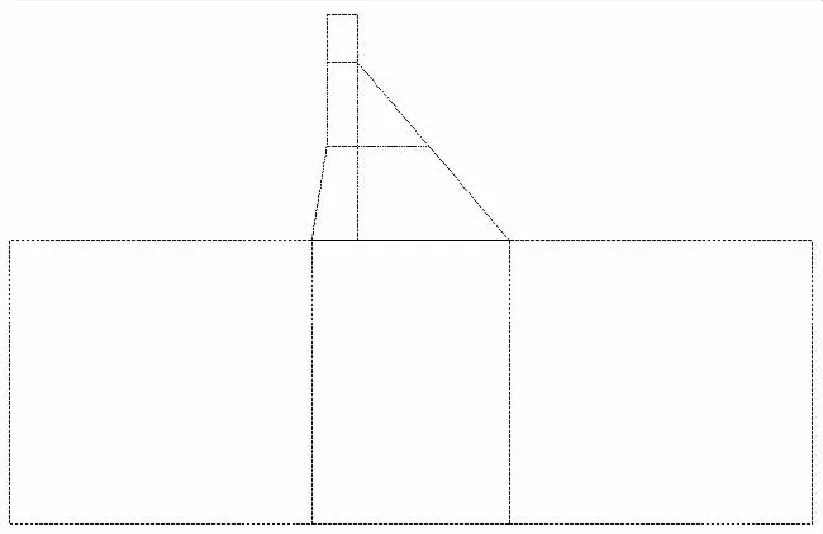
图2 大坝非溢流坝段实体模型图
2.3 网格划分
网格化分:本工程为平面应变问题,采用四结点等参单元。划分网格时,在应力集中区域(坝踵和坝趾附近等),因为应力变化剧烈,故将网格划分得小一些。单元的形状尽量避免小锐角和大钝角的出现,边长也不宜太大。坝体共分1902个单元,如图3所示。

图3 网格图
2.4 加载
大坝作用力有自重、水压力、泥沙压力、扬压力和地基受到的水压力等。其中自重以惯性力的形式施加,水压力、泥沙压力及扬压力以分布力的形式。力施加完后,就进行求解和后处理。
2.5 结果分析
(1)坝体应力分析
校核洪水情况时,模型σ1、σ3等值线如图4—5所示。

图4 校核洪水情况σ1等值线图
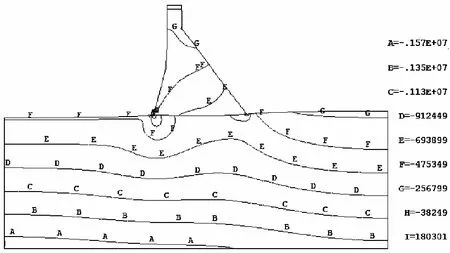
图5 校核洪水情况σ3等值线图
坝趾处最大压应力为750.53kPa<6.7MPa,因此满足材料强度要求。坝踵最大拉应力虽为485.030kPa>0,但这是由于应力集中造成的,可通过将该处网格细分或增加单元的结点来减小应力的求解值。也可根据拉应力范围来进行复核,根据规范坝体铅直方向的应力在计入扬压力时需满足坝体上游面拉应力区宽度易小于计算截面宽度的7%(铅直拉应力宽度/计算截面宽度),经计算,受拉区宽度与计算截面宽度的比值2.55%<7%,所以大坝应力满足强度要求。
(2)坝体变形分析
校核洪水情况时的变形及位移如图6—9所示。
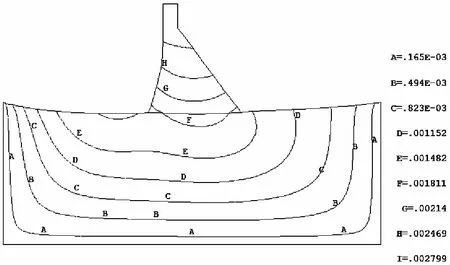
图6 校核洪水情况位移等值线图

图7 校核洪水情况x方向位移分量等值线图
经过后处理可知,校核洪水情况,结点2128(即坝顶上游侧)向下游发生的位移最大为19.613mm;结点747(坝踵处)沉降量最大为20.33mm;结点2127(即坝顶下游侧)的总位移也最大,为27.0mm,坝体各处变形亦均在允许范围(47820/650=73.70mm)之内。
根据图9中可知,由有限单元法分析的大坝变形与实际相符。自重使大坝整体下沉,但由于计算

图10 坝基单元划分

图8 校核洪水情况y方向位移分量等值线图

图9 校核洪水情况变形对比图
模型坝基上、下游所受水压力不同,出现了上游坝基比下游坝基y负方向偏移量大,变形明显。水平水压力使坝体向下游偏移,坝踵处位移较小,坝顶处由于坝体的位移的叠加位移值最大。
(3) 坝基抗滑稳定分析
通过有限元法计算,可以求解出坝体及坝基各个单元的应力和剪力,本次通过LIST文件显示出坝基各节点的应力和剪力。坝基上共分了40个节点,39个单元,如图10所示。各节点的应力的剪力结果见表3。
根据公式(8),计算得校核水洪水位时坝基的抗滑稳定安全系数为5.45,大于SL319—2005要求的2.5,则坝基的抗滑稳定满足要求。
3 结论
(1)本文简要介绍了有限元基本原理和步骤,并寻求了一种计算简单、便于应用的潜在滑动面抗滑稳定安全系数计算方法。
(2)根据计算结果可知,由于上游坝踵应力集中出现了拉应力,而用极限状态设计法计算该断面不出现拉应力;根据变形云图,可知有限单元法分析的大坝变形与实际相符;可通过LIST文件显示出各潜在滑动面的节点应力和剪力,根据公式求出各层的抗滑稳定系数。
(3)本文重点探讨了有限元法在大坝应力、变形及抗滑稳定计算分析中的应用,通过可视化软件界面能更直观的展现出坝体的应力、变形云图,是有效可行的一种设计方法,可弥补传统刚体极限平衡法的不足。

表3 坝基单元节点应力和剪力计算表
