泰森多边形距离反比加权法在BTOPMC模型中的应用分析

马亚丽，敖天其，王汉涛

(1.甘肃农业大学 水利水电工程学院，甘肃 兰州 730070；2.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065；3.中国长江三峡集团公司，湖北 宜昌 443133)

我国监测的雨量以点雨量为主，产流计算过程要求将点雨量转化为面雨量，为此，通过对雨量数据进行插值得到每一个网格计算单元的雨量值。目前，并不存在某一个降水插值模型能够适应诸多分布式水文模型，当然这也是水文学界的一个重要难题，因此针对某一个特定的水文模型，探讨某种雨量插值方法对其模拟精度以及参数的影响变化规律是有一定意义且十分必要的，不仅可以提高模型模拟的效果，而且更有利于我们深入地认识该水文模型。朱会义等[1]采用反距离加权插值法、克里金插值法、样条函数插值法等，根据潮白河流域58个雨量站1990年的降雨观测数据，得到插值结果的不确定性与雨量站个数成反比、与时间尺度成反比。陈艳英等[2]用样条函数法、克里金内插法及距离平方反比法，对温州地区1991—2001年90个观测站的月平均降雨进行雨量插值，结果表明各种方法效果均较好，距离平方反比法精度误差较小。覃建明等[3]提出了基于泰森多边形法法估算流溪河模型单元网格面雨量的方法，通过分析六场实测洪水过程的模拟效果，说明泰森多边形法适用于流溪河模型洪水预报降雨估算的需要。李金洁等[4]以西南地区1996—2000年93个气象台站观测的月均降雨量为基础，采用反距离加权法(IDW)和普通克里金(O-Kriging)两种方法进行空间插值，通过交叉验证结果对两种方法进行分析比对，结果表明：在降雨量的空间插值中，由于研究区域和时间尺度的不同，并不存在绝对的最优方法，应根据实际应用效果选择最适合的方法。汪青静等[5]采用4种空间插值算法对研究区2006—2014年的日降雨进行插值，并将面均雨量作为新安江模型的输入，分析和比较其降雨径流响应，建议选用计算简便的插值算法计算面雨量，比如泰森多边形、反距离权重法。本文为了探究泰森多边形的距离反比加权法与BTOPMC水文模型自带的最邻近插值法对洪水模拟效果的影响差异，利用泰森多边形的距离反比加权法对BTOPMC水文模型降雨空间插值方法进行改进，并对两者的模拟效果进行比较分析，以期提高BTOPMC模型洪水模拟的可靠性，从而进一步改进和完善BTOPMC模型，为将来深入研究该模型和广泛应用该模型奠定一定的基础。

1 BTOPMC模型简介

BTOPMC(Block-Wise use of TOPMODEL with Muskingum-Cunge Method)模型是一个基于物理机制的分布式流域水文模型[6- 7]，具体需要率定的参数个数少、且全部具有物理意义等显著优点。BTOPMC模型已在国内外得到一定程度的推广和应用，在日本的富士川流域，黄河流域[8]、印尼的 kali Brantas 流域、尼泊尔的8个流域[9]以及美国的十几个中小型流域取得了较好的验证。模型采用TOPMODEL作为基本的产流子模型、Muskingum-Cunge(马斯京根—康奇法) 作为汇流子模型，并加入了由敖天其等开发的洼地处理、河网生成和自然子流域划分等有关地形解析的子模型[10]。BTOPMC主要子模型组成结构如图1所示。目前模型主要有5个参数：饱和土壤导水率T0(m2/s)、饱和土壤导水率的衰减因子m(m)、根层最大储水量Srmax(m)、平均土壤饱和差初始值Sbar0(m)、曼宁糙率系数n0。其中Srmax主要反映植被/土地利用的影响，T0和m反映流域土壤种类的影响，Sbar0主要反映流域地形的影响，n0同时反映土壤种类和植被/土地利用的影响。其中，前4个为产流子模型中的参数，n0为汇流子模型参数，这些参数都具有明确的物理意义。Srmax、T0、m、n0是以每一个DEM网格来率定的，而Sbar0(k)是以每一个子流域来率定的。

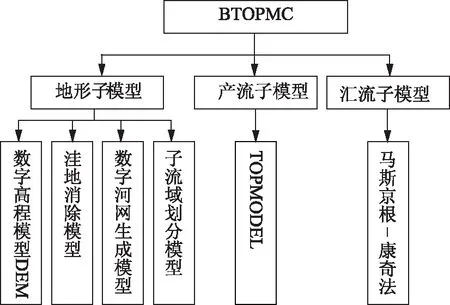
图1 BTOPMC主要子模型组成结构

BTOPMC模型采用了两个精度评价指标进行模型评价：Vr和E。

Vr是总模拟流量(TVsim)与实际资料观测值(TVobs)之比，公式如下：

Vr=TVsim/TVobs

(1)

Nash效率E[11- 12]，计算公式如下：

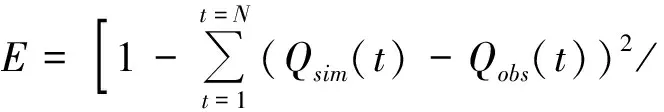
(2)

式中，N—时间步长的总数；Qsim—时间步长的模拟流量；Qobs—时间步长的观测流量；Qav—是整个时期的观测流量平均值。

Nash值越高则表明模拟效果越好，100%代表模拟结果与实测资料完全一样。

除了以上两个评价指标，可以根据具体需要，采用模拟和观测洪峰时间及平均流量等其他参数作为辅助的评价指标。

2 泰森多边形的距离反比加权法与BTOPMC模型的耦合

2.1 泰森多边形的距离反比加权法

距离反比加权法(IDW)也叫反距离加权法，是一种常用的加权平均插值方法，由Shepard[13]最早提出。该法将计算区域划分成若干矩形网格，每个网格的宽度和长度分别为Δx和Δy，各网格点的雨量Zj由周围邻近的雨量站实测资料按距离平方的倒数插值求得[14]。每个DEM网格点与所有已知的雨量站点的权重之和为1，各雨量站的贡献值(即权重)随该DEM网格点与各雨量站的距离增大而减少，公式如下：

(3)

式中：Zj—第j个待插值DEM网格点的雨量值，(j=1，2，3，…，n)；Zi—第i个已知雨量站点的雨量值，(i=1，2，3，…，n)；n—流域内已知雨量站总数；Di—待插值DEM网格点与第i个雨量站点的距离；p—距离的幂，距离反比加权法中p=2。

泰森多边形法是一种极端的边界内插方法，将各雨量站两两相连并作连线的中垂线，中垂线相交所形成得若干个多边形即为泰森多边形。以泰森多边形内仅有的一个气象站的雨量值来代表这个多边形区域内的降雨量。利用泰森多边形法将流域划分为多个子流域，对每个泰森多边形内的所有已经利用距离反比加权法插值的DEM网格点的雨量求平均值，即为泰森多边形的距离反比加权法。以每个泰森多边形为单位，对经过距离反比加权法插值的DEM网格点雨量值进行雨量平均，计算公式如下：

(4)

式中，pk—第k个泰森多边形内的的平均雨量，(k=1，2，3，…，n)；Zj，k—第k个泰森多边形内第j个DEM网格的雨量值，j=1，2，3，…，n；nk—第k个泰森多边形内的DEM网格个数，k=1，2，3，…，n；k—泰森多边形的编号；j—DEM网格的编号。

泰森多边形的距离反比加权法结合了距离反比加权法和泰森多边形法两种降雨插值方法，使各雨量站对流域内所有DEM网格点的雨量值都有贡献，却又不会影响BTOPMC模型的结构，便于与BTOPMC模型的耦合。

2.2 与BTOPMC模型的耦合

在分布式水文模型BTOPMC中，敖天其等采用的降雨插值方法为最邻近插值法，即每个DEM网格点的雨量值采用距离该DEM网格点最近的那个雨量站的雨量值，并且将每个DEM网格点最近的雨量站编号存储在以后缀“*.sit”的文件中，结合存储在“*.pri”文件中对应雨量站的雨量值，从而可以得到每个DEM网格点的雨量值，值得注意的是在“*.pri”文件中每一列对应一个已知雨量站点各时刻的雨量，每列的编号与雨量站的编号一致。

本文为实现泰森多边形的距离反比加权法与BTOPMC模型的耦合，首先利用泰森多边形法将流域划分为多个子流域并依次编号，每个泰森多边形内的DEM网格点均采用该泰森多边形的编号，DEM网格点编码信息存储在后缀为“*.sit”文件，通过距离反比加权法对各DEM网格点的雨量值进行插值，每个泰森多边形内内所有DEM网格的雨量值逐时刻求平均值代表该子流域的雨量，并存储在后缀“*.pri”文件中，泰森多边形的编号与“*.pri”文件的列编码相对应。

3 改进的BTOPMC模型在明江流域的应用

3.1 明江流域及资料概况

渠江(渠河、南江河)是嘉陵江的一条支流，发源于川、陕两省交界处的米仓山，流经南江、渠县、广安、邻水等县境，在合川市汇入嘉陵江，并最终流入长江。总流域面积3.92万km2，多年平均流量约为663m3/s，多年平均径流量约为235亿m3，河道主干流长约305.5km，天然落差532m，干流平均比降0.17‰。明江为渠江的二级支流，河长93km，流域面积1204km2，河口流量25.6m3/s，总落差1155m。渠江流域大部分属亚热带湿润季风气候，年降水量在1014～1500mm以上，雨季主要集中在7—9月份，占全年降雨量的50%以上。本文研究区域位于明江上游赶场(二)水文站以上，控制流域面积约273km2，多年平均流量7.54m3/s，水位变幅5.9m。明江水系图如图2所示。

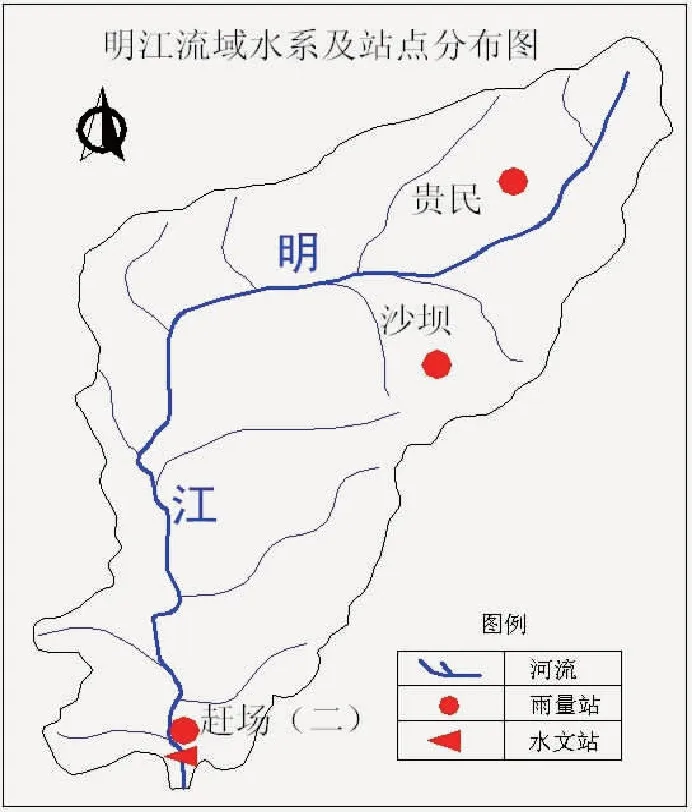
图2 明江流域水系图

BTOPMC模型径流模拟所需数据资料见表1。该研究范围内收集了3个雨量站和1个水文站资料，由中国气象局成都高原气象研究所提供：赶场(二)、贵民、沙坝雨量站；赶场(二)水文站。水文站与雨量站基本情况见表2。

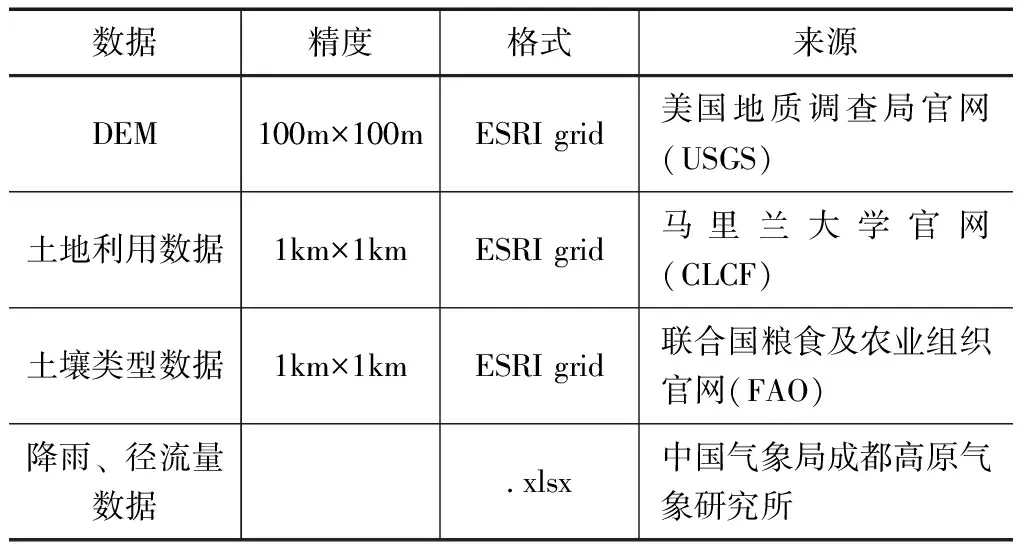
表1 模型所需数据资料

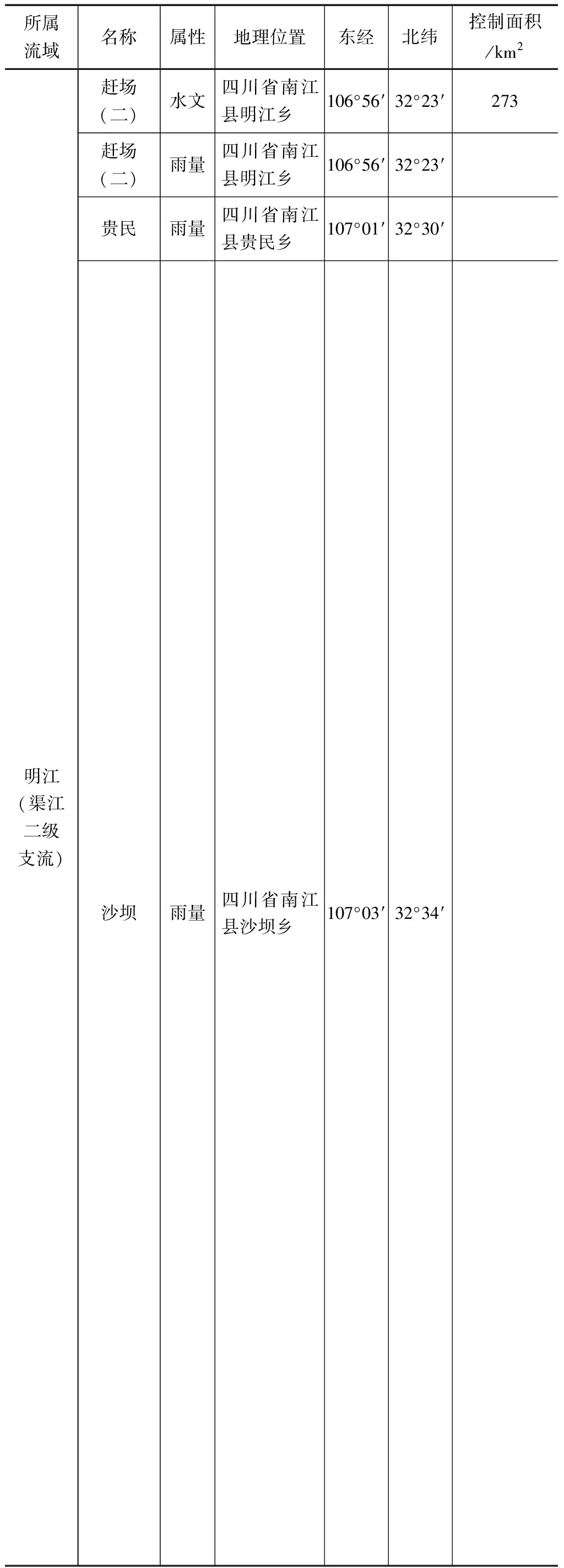
表2 水文站及雨量站基本情况表

3.2 参数率定和验证的结果与分析

本文采用赶场(二)(2007/7/2 1∶00～2007/7/8 0∶00)的洪水数据进行BTOPMC模型参数的率定；利用赶场(二)(2004/9/29 1∶00～2004/10/3 0∶00)的洪水数据进行BTOPMC模型参数的验证。根据BTOPMC模型精度评价指标要求，结合本文洪水模拟的特点，选用以下4个评价指标对模拟结果进行评价，包括：Nash效率(E)，模拟总径流量与实测总径流量之比(Vr)、模拟洪峰时刻与实测洪峰时刻之差(ΔQt)、模拟洪峰洪量与实测洪峰洪量的相对误差(ΔQmax)，率定期和验证期的的评价指标值见表3。

通过模拟结果比较分析，可以看出，在参数率定过程中，模型自带的最邻近点插值法Nash效率高于泰森多边形的距离反比加权法Nash效率，但是在验证过程中，泰森多边形的距离反比加权法Nash效率高于最邻近点插值法Nash效率，同时，泰森多边形的距离反比加权法模拟洪峰时刻与实测洪峰时刻相吻合，对洪峰时刻的模拟效果更准确，模拟洪峰流量与实测洪峰流量相对误差更小，可见，在更为注重对洪峰时刻及洪峰流量的模拟效果的洪水模拟中，泰森多边形的距离反比加权法优于模型自带的雨量插值方法，对BTOPMC模型降雨插值方法的改进，有利于提高模型对于洪水模拟的精度。

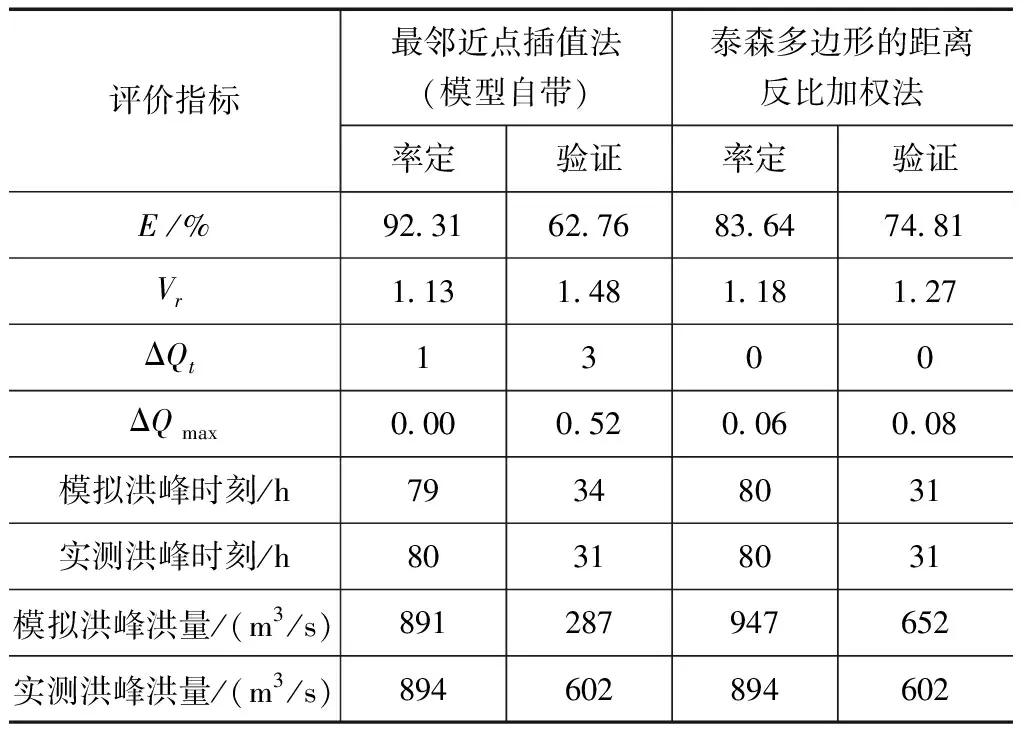
表3 明江流域水文断面参数率定和验证评价指标值

模型自带的最邻近点插值法与泰森多边形的距离反比加权法两种雨量插值方法对洪水过程的形态变化影响不同，相比之下，泰森多边形的距离反比加权法对洪峰流量、洪峰时刻的模拟效果更佳。率定期洪水过程线如图3—4所示，验证期洪水过程线如图5—6所示。

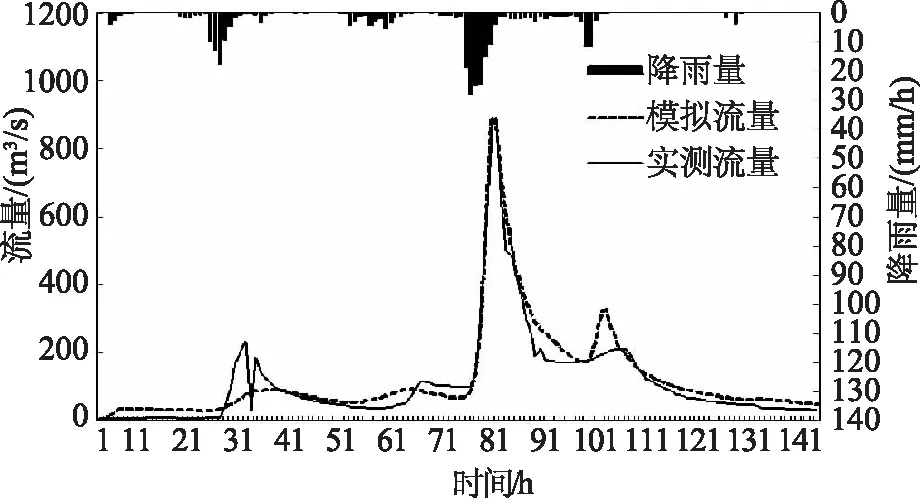
图3 率定期洪水过程线(模型自带最邻近点插值法)

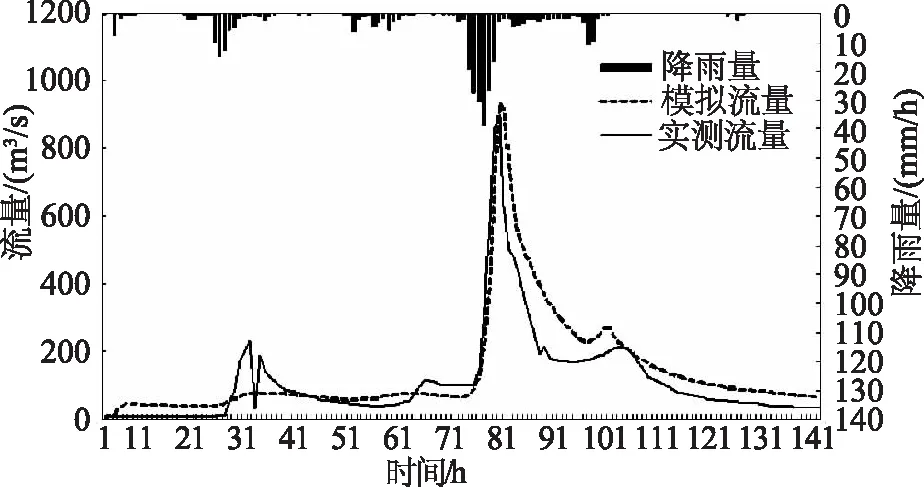
图4 率定期洪水过程线(泰森多边形的距离反比加权法)

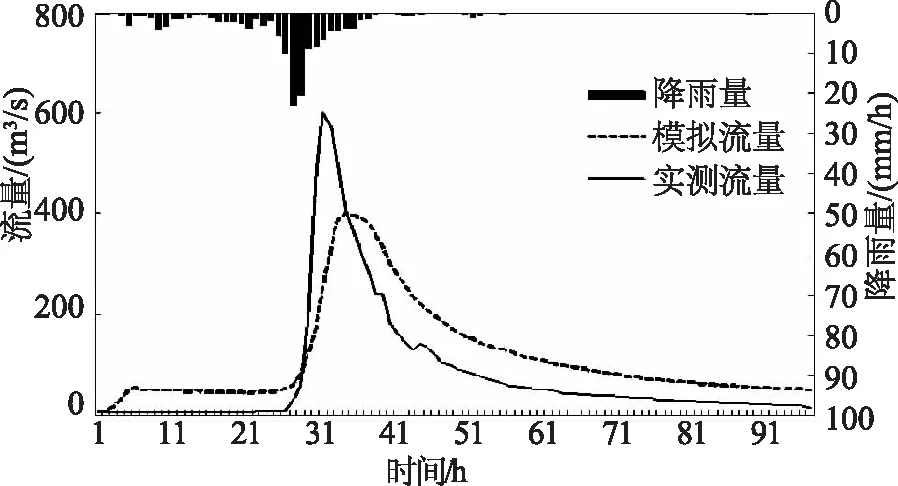
图5 验证期洪水过程线(模型自带最邻近点插值法)

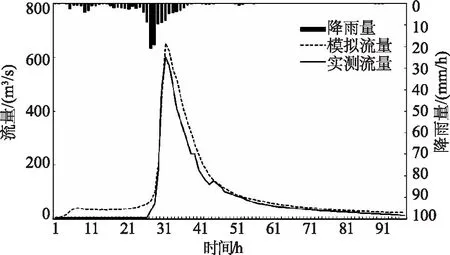
图6 验证期洪水过程线(泰森多边形的距离反比加权法)

BTOPMC模型主要有5个参数，具有需要率定的参数个数少、且全部具有物理意义等显著优点，并且模型采用SCE-UA优化算法对参数进行率定并

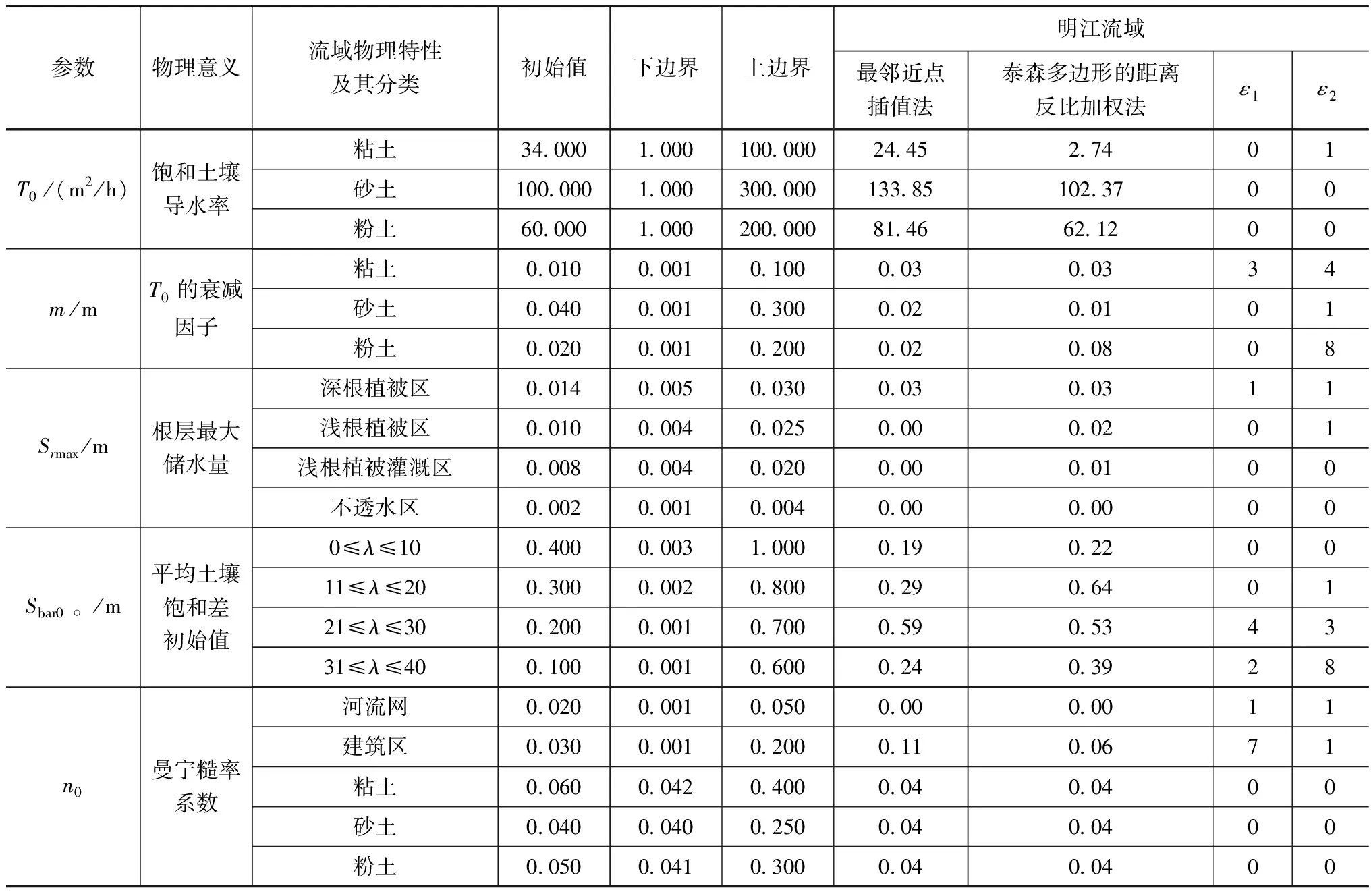
表4 明江流域水文断面模拟参数自动优化值

确定最终参数值，模拟参数自动优化值具体见表4。因目前模型并不具有参数敏感性分析模块，本文通过增加模型参数的初始值和上下限，并以此为参照，与两种降雨插值方法自动优化确定的参数进行比较，依据两种方法的参数变化幅度，找出变化最大的参数值，以相对误差η的平方ε表示，ε保留整数部分，公式3如下：

(5)

式中，εi—相对于初始值对应参数的相对误差平方，ε1最邻近点插值法；ε2泰森多边形的距离反比加权法；x0—模拟参数初始值；xi—两种降雨插值法模拟参数自动优化值。

采用最邻近点插值法，模型参数曼宁糙率系数(建筑区)受雨量插值方法的影响最大，Sbar0(21≤λ≤30、31≤λ≤40)、m值(粘土)受雨量插值方法的影响较大；采用泰森多边形的距离反比加权法，模型参数m值(粉土)、Sbar0(31≤λ≤40)受雨量插值方法的影响最大，m值(粘土)、Sbar0(21≤λ≤30)受雨量插值方法的影响较大，这说明了BTOPMC模型的各参数是具有一定物理意义的。

4 结论

本文采用泰森多边形的距离反比加权法对BTOPMC模型的降雨空间插值方法进行改进，改变模型自带的最邻近点插值法仅仅考虑最近雨量站的雨量代表DEM网格点雨量值的局限性，而采用泰森多边形的距离反比加权法的雨量插值方法，使得所有已知雨量站均对某DEM网格点雨量值有贡献，通过比较两种降雨量插值方法在明江流域洪水过程的模拟结果，可以看出，在更注重对洪峰时刻及洪峰流量的模拟效果的洪水模拟中，泰森多边形的距离反比加权法优于模型自带的雨量差值方法，通过对BTOPMC模型降雨插值方法的改进，有利于提高BTOPMC模型洪水模拟精度，对洪峰流量、洪峰时刻有较好的模拟；采用最邻近点插值法，模型参数n0(建筑区)受雨量插值方法的影响最大，Sbar0(21≤λ≤30、31≤λ≤40)、m值(粘土)受雨量插值方法的影响较大；采用泰森多边形的距离反比加权法，模型参数m值(粉土)、Sbar0(31≤λ≤40)受雨量插值方法的影响最大，m值(粘土)、Sbar0(21≤λ≤30)受雨量插值方法的影响较大，这说明BTOPMC模型的各参数是具有一定物理意义的。

本文利用泰森多边形的距离反比加权法对BTOPMC模型的降雨空间插值方法进行改进，并取得一定成果，但是雨量插值方法在不同时间尺度上对模型的影响、不同的DEM分辨率下雨量插值方法对BTOPMC模型的影响等还需要进一步探讨。