基于参数自适应动态差分进化算法的变压器局放源定位

吴志祥，黄旭聪，施小帅，李晓健，闵静静

（国网浙江省电力有限公司宁波供电公司，浙江 宁波 315010）

0 引言

局部放电（以下简称“局放”）是电力变压器绝缘老化的表现形式之一，同时也是绝缘进一步劣化并导致绝缘失效的主要原因之一[1-3]。为了保证电力变压器安全可靠地运行，需要定期对电力变压器进行有效的局放检测。

不同于传统的局放电测法，局放超声法由于具有抗干扰性能强、定位精度高等优点开始逐渐应用于电力变压器的局放检测[4-5]。为了实现电力变压器局部放电源（以下简称“局放源”）的精确定位，文献[6]提出了一种复数域牛顿迭代搜索算法，较好地解决了实数域中时间差误差导致的无解情况，但存在寻优初值难以选取的问题。为了避免初值选取对局放源定位的影响，大量的智能算法开始得到应用[7-8]。文献[9]提出了一种融入模拟退火思路的自适应粒子群混合算法，有效解决了传统粒子群算法存在的全局寻优能力较差及早熟问题，从而提高了定位精度；文献[10]将序列二次规划引入遗传算法并成功应用到变压器局放源定位中。

虽然混合优化算法能够一定程度地解决传统优化算法存在的局限性，但其本身也存在寻优参数较多、寻优过程较复杂等不足，从而限制了此类方法在实际变压器局放源定位中的应用[11]。对此，为使寻优参数设置简单化，同时提高算法的全局寻优能力并加快收敛速率，本文对传统DE（差分进化）[12]算法引入参数自适应调节及动态更新策略，从而有效提高了DE 算法的寻优性能。通过Benchmark 测试函数和实际变压器局放超声定位对该方法的可行性和有效性进行了验证。

1 DE 算法

1.1 基本DE 算法

对于D 维实数空间的最小化优化问题，DE算法由NP 个D 维实参数向量xiD}构成一个进化种群。在第t 次迭代中首先随机选择其他三个不同的参数向量并将任意两个参数向量形成的差分向量通过比例因子F 缩放后加到第三个向量上形成目标向量的变异向量即：

式中：r1≠r2≠r3≠i；缩放因子F 分布于[0，2]。

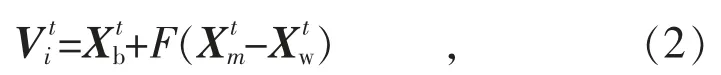
式中：rand 产生[0，1]的随机数；CR 为分布于[0，1]的交叉概率因子；表示向上取整。

最后利用“贪婪”搜索策略对试验向量进行选择并更新至下一代，即：

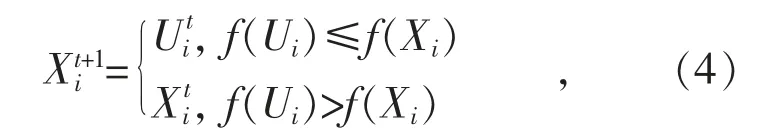
式中：f（·）为适应度函数。

服务器端接收用户分享的自定义规则，暂时存放在共享恶意流量规则库中。用户可以试用共享规则库中的规则并对其评价打分。服务器定期将高评分规则加入公共恶意流量规则库中，向所有客户端同步。随着用户的分享和数据库的不断更新，逐步加强对恶意流量拦截的广度和准确度。

1.2 参数自适应动态DE 算法

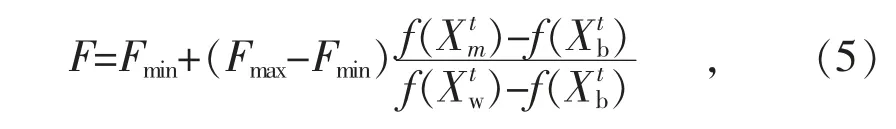
式中：Fmin和Fmax分别为设置的缩放因子的最小值和最大值。由式（5）可知，当相距较近时，F 取值较大；当相距较远时，F 取值较小。

进一步分析交叉操作方程式（3）可知，当交叉概率因子CR 较大时，变异向量对试验向量的贡献越多，从而容易导致适应度较好的个体遭到破坏；而当CR 较小时，又不利于产生新的个体，虽然可保持较好的全局搜索能力，但也会减慢收敛速率。

为了同时兼顾全局搜索能力和加快收敛速率，利用适应度函数自适应控制交叉概率因子CR的变化，如式（6）所示。

式中：CRmin和CRmax分别为设置的交叉概率因子的最小值和最大值；fmin和fmax分别为当前种群中适应度的最优值和最差值；为当前种群适应度的平均值。

由式（6）可知，当个体适应度大于平均适应度时，由于当前个体性能较差，因此交叉概率因子取较大值，反之则反。

由1.1 节DE 算法可知，在DE 进化的过程中，每个种群始终保持不变直到被下一代替代，因此导致DE 算法收敛速率较慢。为了加快收敛速率，采用文献[13]提出的动态DE 策略如式（7）所示：

2 Benchmark 函数测试

为了验证PADDE（参数自适应动态差分进化）算法的寻优能力，选取2 个典型的标准测试函数Rastrigin（f1）和Ackley（f2）进行测试，函数表达式如表1 所示，对应的函数图形如图1 所示。

表1 标准测试函数

图1 测试函数

对于DE 算法，选取F=0.5，CR=0.5；对于PADDE 算法，选取Fmin=0.1，Fmax=0.9，CRmin=0.1，CRmax=0.6。种群规模NP=30；2 个测试函数迭代次数分别设置为50 和100。同时为减少随机性的影响，每个测试函数2 种算法均独立运行50 次，得到统计结果分别如表2 所示。由表2 结果可知，对于测试函数f1和f2，PADDE 的寻优精度均高于DE。

表2 DE 及PADDE 寻优结果对比（50 次平均值）

3 变压器局放源定位

3.1 基本原理

由于变压器呈立方体结构，因此为了实现变压器局放源的定位，通常需要利用多个位于不同位置的超声传感器结合局放信号TDOA（到达时间差）进行估计。

考虑图2 所示变压器局放源定位模型，假设局放源坐标为P（x0，y0，z0），局放超声传感器的坐标为S（xi，yi，zi），i=1，2，3，4。结合局放信号传播原理可得到式（8）所示方程组：

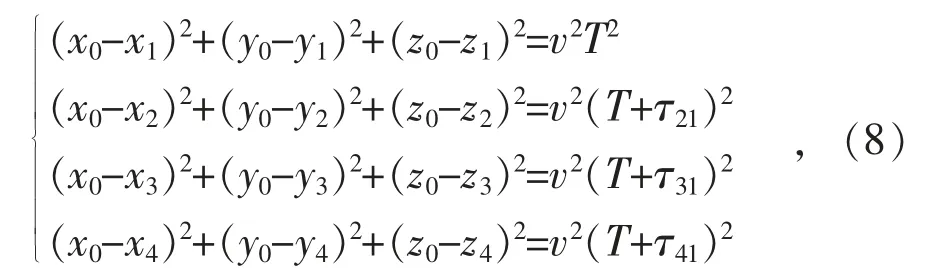
式中：T 为局放信号传至超声传感器S1的时间；v 为变压器油中超声波波速；τi1为其他超声传感器与传感器S1接收到的超声信号的时延估计值，i≠1。

图2 变压器局放源定位原理

进一步分析式（8）可得到如下方程：

由于式（9）为超定方程，难以获得精确解，因此通常转化为寻优问题进行求解。考虑到实际中的约束条件，得到优化问题如式（10）所示：

式中：‖·‖为2 范数；Lx，Ly和Lz分别为变压器的长、宽、高。通过式（10）结合寻优算法即可实现变压器局放源的定位。

3.2 算例分析

为了验证PADDE 算法对变压器局放源的定位效果，分别选取文献[14]中3 组数据进行模拟，其中变压器长、宽、高分别为1 000 mm，1 000 mm，800 mm，实际局放源坐标为P（610，320，350），单位为mm（下同），且均以1 号传感器为参考，各组数据具体情况如下：

（1）4 个超声传感器坐标分别为S1（0，200，400），S2（0，600，300），S3（300，1 000，200），S4（600，1 000，500）；时延τi1=[36，100，53]，i=2，3，4，单位为μs（下同）。

（2）4 个超声传感器坐标分别为S1（0，510，420），S2（300，1 000，600），S3（1 000，450，350），S4（840，0，450）；时延τi1=[103，-166，-169]，i=2，3，4。

（3）4 个超声传感器坐标分别为S1（0，300，500），S2（200，1 000，520），S3（1 000，600，400），S4（600，0，480）；时延τi1=[132，-104，-202]，i=2，3，4。

种群NP 设置为50，迭代次数设置为500，得到两种算法的定位结果如表3 所示。由表3 结果可知，基于PADDE 算法的定位精度高于DE，且定位误差较小，满足工程应用。

4 结论

本文提出了一种基于PADDE 算法的变压器局放源定位方法，具有以下优势：

表3 局放源定位结果对比

（1）相比于传统DE 算法，PADDE 算法由于利用适应度函数对参数进行了自适应调节，因此具有更强的全局寻优能力以及更快的收敛速率，其寻优结果更加精确。

（2）将PADDE 算法应用于变压器局放源定位中，其定位精度高于DE 算法，且定位误差较小，具有一定的工程应用价值。