基于图形分析的初中几何变式教学研究

石贝娜

摘要：初中几何教学是学生思维能力的良好锻炼，但在几何学习中，教师的教学方法直接影响学生的学习效果。几何是中学生学习的一门新学科，因此基础图形理解的学习能力较低，教师需要在图形分析的基础上深入研究学校几何变式的教学。

关键词：图形分析;初中几何;变式教学

引言

初中几何教学是学生思维能力的良好锻炼，但在几何学习中，教师的教学方法直接影响学生的学习效果。几何是中学生学习的一门新学科，因此基础图形理解的学习能力较低，教师需要在图形分析的基础上深入研究学校几何变式的教学。

1.初中几何变式教学应用价值

在初中几何教学中，几何变式教学必须以教材为基础，考虑学生的主体性，能够充分利用几何，呈现逆向教学优势，是一种有效的数学教学方法，具有较好的教学效果，能激发学生的学习兴趣，提高其抽象思维能力。变式教学是一种以几何为基础的教学模式，以学生为主体，从不同角度转换几何概念，让学生深入理解和掌握抽象知识。变式教学中，学生可以通过类比、联想、辩证法等反思方法发展抽象思维能力，鼓励学生发展良好的思维方式。此外，变式教学具有一定的开放性，促进了学生的创新能力，同时有助于培养和提高学生的自主学习能力，这是学生在未来学习过程中的重要能力。

2.初中几何教学涵义

初中几何教学是打开学生数学思维大门的最佳钥匙之一，许多学生，即使原有的数学基础不牢固，也能很快进入几何学习状态，因为他们有很强的思维能力，这种思维能力极大地激发学习数学的兴趣，提高数学的整体学习水平。同时，几何教学对学生的主要吸引力在于严格的逻辑推理和变化的形式，因此，几何教学一直倾向于以图形变换和多种解决方案为特征的变体的教学，以及如何在新的教学形势下更有效地传播这种教学方式。介绍数学概念的变式，大多数数学概念都是抽象的，为了提高学生对数学变体的理解和学习，教师可以向学生展示他们在生活环境中的材料。例如，在研究平行四边形的概念时，老师可以举出学生熟悉的生活例子：白板、门框、石膏盒以及图形等。然后总结和概括这些元素的特征，提高对平行变式概念的视觉理解。有关详细分析，请参见下文。

3.在教学过程中的几何变式教学

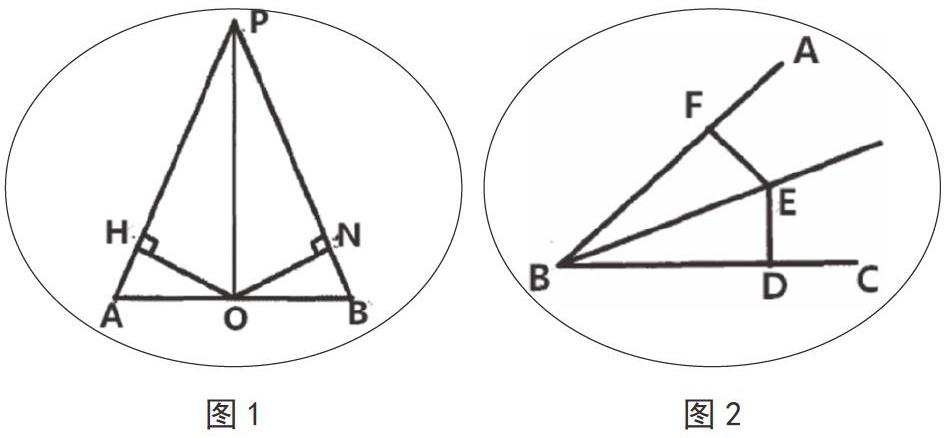
初中几何教学的过程主要是正确引导学生，把实际问题转化为几何思维的过程，即针对教学过程和定理解释中遇到的具体信息问题提炼抽象公式。这一过程提高了学生的数学思维和思维能力，并显著提高了学生对数学知识的运用。在教学中，教师可以运用变量和多种模式的教学方法来激发学生学习数学几何的兴趣，引导学生在回答问题的领域以不同的方式进行，促进学生的创新和发散思维的培养。比如，在求证这样一道题的时候（如图1）：

如图1所示，在图形?APB之中，三角形AP=BP、OH⊥PA、ON⊥PB三角形足分为H、N，点O，在三角形AB中如果假设PO点位三角形的高，以此来求证OH=ON。

例如：这道题，在学生的定向思维中会出现很多种解题方式，同时学生会在不同的知识点以及题目的数据进行分析得出不同的解题方法。一般来说，许多学生使用等腰三角形三线合一法的性质的组合解题，这是最简单的方法，但是教师必须指导和恰当地引导学生应用不同的解决方案来证明问题。教师可以引导学生运用等角等值知识，对角a角b进行论证，然后结合等角三角形的腰三角形三线合一，接着将?HAO≌?NBO进行证明，然后将OH=ON证明出来。虽然许多学生不熟悉三线合一知识点，但教师应该始终要求学生以不同的方式回答问题，不要让学生养成简单应对方法和手段的习惯，应该注重培养学生的创新意识。

4.基于图形分析的初中几何变式教学

在几何教学中，学生经常混淆与其思维方式直接相关的概念，这些概念不仅抽象，而且更具逻辑性和系统性，如果学生在学习过程中不理解概念的本质和意义，就无法解决相关的几何问题。

例如，在研究八年级课本中的“线段的垂直平分和角平分线的性质”时，有一些学生对这两个概念的理解思维模式比较混乱。一些学生认为角平分线上的点到两端的距离相等，但在表达角平分线性质时，通常缺少两个垂直点的遗漏问题。如图2：

角平分线性质所示，学生经常将其表述为：BE平分角ABC，∴EF=ED。教师在对学生进行纠正引导的时候就可以采用变式教学，通过让学生反复理解垂直平分和角平分线的定理和知识点，正确理解这两个定理，即使得出距离相等的结论，也可以正确区分这两个不同的平分线距离。在解题中角平分线中的位置点以及角两边直线之间的距离，就是垂直平分线点到线两端之间的垂直距离，等同于两点之间的距离。教师在课堂教学中要运用变式类比来引导学生，让学生充分的理解角平分线以及垂直方式的正确解题思路，在学生对两者之间的理论以及定理能够区分认识之后，在进行解题，那么在解题中就会较少上述问题的发生，同时也会对学生的创新思维以及解题技巧进行相应的提高与培养。

结语

总之，初中数学改革教学是新课程改革下数学教育发展的新趋势。发挥重要作用提高中学数学教学效果，促进学生数学学习。在初中几何习题教学中，应坚持“永不改变原则”的原则，努力把握学生主体的关键，教学改革应从拓展学生思维的角度进行。为了在此基础上深化学生的思维，初中数学教师有必要在教学中更新数学教学观念，发现数学变式教学的特点，引导学生以不同的方式解決数学问题，从而促进学生数学学习的进步。

参考文献：

[1]程建云.初中几何教学中习题变式的应用探析[J].理科爱好者（教育教学版），2014，6（3）：82.

[2]刘兴旺.习题变式在初中几何教学中的应用研究[J].求知导刊，2014 （4）：141.

[3]张青.浅谈初中几何单元复习课变式题组教学设计[J].理科考试研究（初中版），2015，22（5）：13-14.