命题要注意表达的规范性
——对一道中考选择题的思考
2019-12-06安徽省砀山县高铁新区道南初中235300王福全
安徽省砀山县高铁新区道南初中(235300)王福全
科学性是命题的灵魂,离开了它中考试题的价值与功能将无从谈起.试题简洁、明了、无歧义是提高试题的科学性的重要因素,下面结合一道中考题谈谈自己的看法.
2017年山东济宁市中考选择题第5 题有两种不同的版本,题目如下.
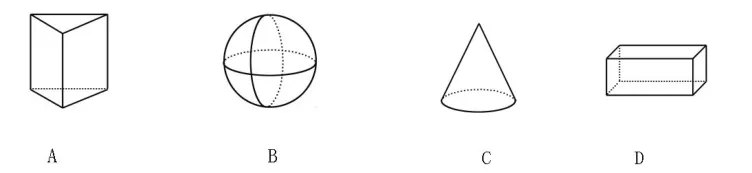
版本1下列哪个几何体,它的主视图、俯视图、左视图都相同的是( )

版本2(全国各省市中考汇编·45 套)[1]下列几何体中,主视图、俯视图、左视图都相同的是( )
一、比较与分析
二者的备选项相同,题干不同.版本1 的设问明确,定量准确,让学生一看就明白,即考查某一个几何体的“三视图”,且三种视图的平面图形相同,这样陈述有利于学生答题,提高了中考题的信度.版本2 的题干“下列几何体中,主视图、俯视图、左视图都相同的是( )”包括以下含义:(1)备选项中的某一个几何体的主视图、俯视图、左视图相同;(2)备选项中有两个或两个以上几何体的三视图相同.此种题干的表述容易产生歧义,不利于学生的思考,学生在获取题干信息的过程中,产生多角度思考导致理解上出现偏差.
二、实践与反思
为了诊断济宁版本2 的题干是否会产生歧义,笔者在我校九年级复习课上进行了一次探究活动.为增强备选项对学生的思考产生干扰,对此题做了修改,题干不变,增加备选项个数,提高了备选项的迷惑性,题目如下:
下列几何体中,主视图、俯视图、左视图都相同的是( ) (请把你认为正确的答案选出)[2]
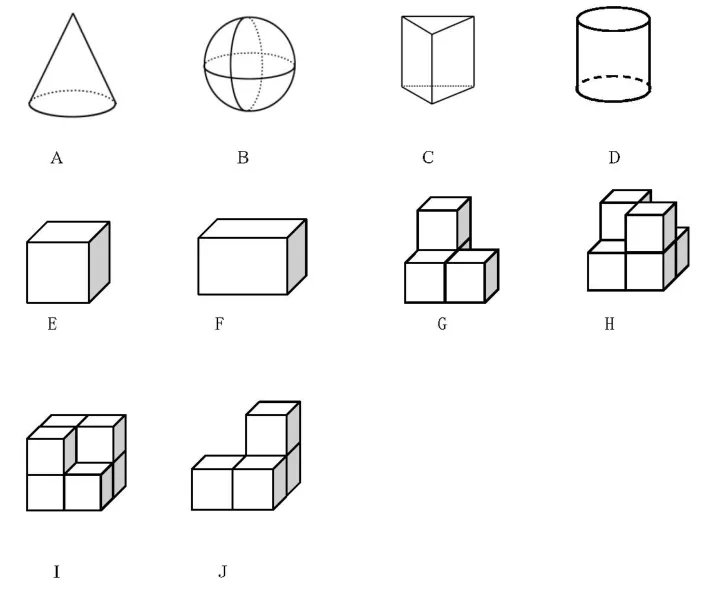
在活动中学生能积极思考,大胆发言,课堂实录如下.教师:(展示练习题)请同学们看大屏幕.学生: 议论纷纷,跃跃欲试.
学生1:选B,因为球的主视图、俯视图、左视图都是圆.
学生2:选E,因为如图放置的正方体,它的主视图、俯视图、左视图都是正方形.
学生1:我把这道题看成单项选择题了.(很懊悔)
学生3:G也是的.
学生4:J也是的吧.
学生:小声议论,众说纷纭.
教师:你能画出G和J的三视图吗? 请生3和生4在黑板上画.
学生:其余学生都开始画了,教室里安静了许多.
学生3:给出G的答案.

学生4:给出J的答案.
学生:都笑了.G是的,J不行.
教师:还有吗?
学生5:H 6 块,I 7 块.
学生6:它们两个块数不一样多,它们两个的主视图、俯视图、左视图不可能相同.
学生7:那不一定!
教师:请学生6、学生7 在黑板上画,其余同学画在作业纸上.
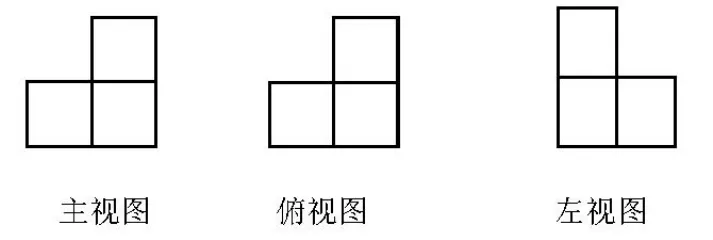
学生:生6、生7 给出相同的答案如下图所示.

教师:同学们,你能发现什么问题?
学生8:H自己的三视图相同,I自己的三视图也相同.
学生9:H的三视图与I的三视图也相同.
学生10:不同的几何体可以有相同的三视图.
学生在解决问题的过程中复习了常见几何体的三视图,以及它们之间位置关系.在探究过程中从考查一个几何体的三视图,循序渐进扩展到两个几何体的三视图.学生对简单几何体的三视图产生思维障碍,经过思考给出了正确答案.在这种题干下学生的思考是多角度的、全方位的,由于九年级的学生已经具备了一定的空间观念和逻辑推理能力,他们对已有的知识经验不在满足,敢于挑战、勇于探索.本次探究活动事先并没有告知本题答案不止一个,实验是有效的.从而可以看出济宁版本2 题干的表述是不适宜的,容易产生认识上的偏差,有失科学性.
三、探索与思考
表述一道试题需要有严谨治学的态度,不能出现漏洞,产生歧义.表述语言力求简洁,准确到位,杜绝科学性错误.我们再来看以下几组试题.
第一组
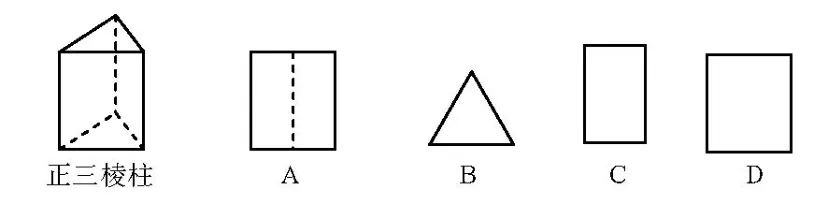
例1(2009年辽宁营口)如图,下列选项中不是正三棱柱三视图的是( )
例2(2017年内蒙古通辽)下列四个几何体的俯视图中与众不同的是( )
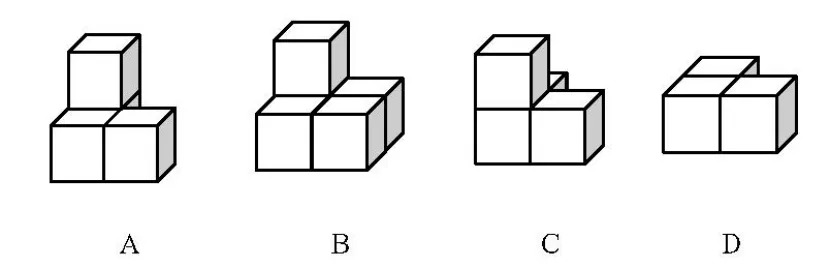
例3(2017年河南省)某几何体的左视图如图所示,则该几何体不可能是( )
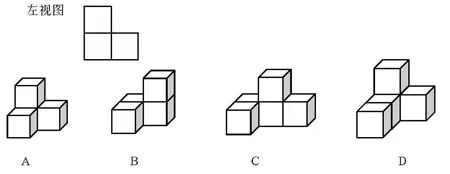
分析对于例1来说,三视图是几何体主视图、俯视图、左视图的统称,三视图是指三个视图所形成的全体图形的集合,而四个选项均为三视图其中的一个视图,题干与备选项之间存在矛盾,所以本题题干的表述在理解上存在歧义,从而影响考试的信度[3].在三视图有关的命题中既要关注命题的条件与结论之间的匹配,又不能违背数学的概念与原理. 再来看例2,命题者可能想让学生根据俯视图的定义选“与众不同”的选项“B”,为了表述的方便,画出对应几何体的俯视图.
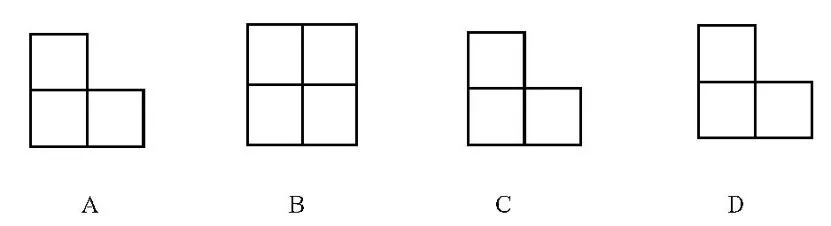
所谓与众不同,即与别人的不一样.对于单项选择题来说,正确的答案有且只有一个.若答案B是正确的,则它的确与众不同,但对于A、C、D来说,则与众相同,其实并非如此.不妨假设选择A,则A与B、C、D选项比较可知,A与B、C、D并不是与众相同.从逻辑上看是矛盾的、不成立的.在这里用与众不同是不规范的、不明确的.命题时不仅要注意题干与备选项中的正确选项的一致,还要注意与错误选项的一致性.不妨利用例3 的表述方式进行改编,题目如下.
某几何体的俯视图,如下图所示,则该几何体不可能是()
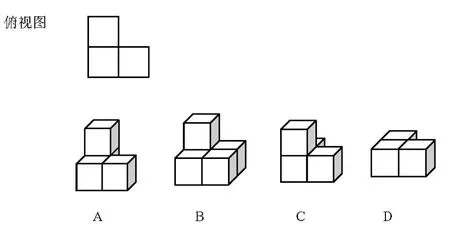
通过对比可以发现例3 的表达方式优于例2,当然对于同一个命题还可以采用其他的命题方式,不在赘述.
第二组
例4(2017年湖南岳阳)下列四个立体图形中,主视图、左视图、俯视图都相同的是( )

例5(2017年辽宁营口)下列几何体中,同一个几何体的三视图完全相同的是( )
A.球 B.圆锥 C.圆柱 D.三棱柱
分析岳阳与营口试题,立意相同,考查的内容完全相同,但呈现的方式不同,即题干的表述不同,备选项所用的语言不同.前者题干与济宁版2有相似性易产生歧义;后者增加“同一个几何体”这一条件,使问题表述的精准到位、毫不含糊、无歧义.但营口试题的备选项采用文字语言表述几何体,不利于学生的思考.如配上图形则试题显得结构和谐,符合数学题的表达方式,更加科学规范.
由以上可以看出济宁(版本1)试题与营口的试题在题干表述上具有如下特点:设问的精巧,表达的简明,逻辑关系自然融洽[4].这样的试题有利于学生,发挥自己的真实水平,提高了试题的效度.命题不拘泥于形式,但要符合语言规则和学科特点.
总之,命题是一种遗憾的工作,没有最好,只有更好.在命题时,恰当使用命题技术,字斟句酌,精益求精,让命题成为经得起考验的宏伟工程.
