九宫格问题新解

雷金化 雷正斌

摘 要：九宫格问题源远流长，其实质属于数独问题。常规解答方法往往不能给出解题的内在逻辑，文献中的解答办法一般又涉及比较高级的数学知识和比较多的抽象思维理解，因此这些方法对低年级学生都不太使用。笔者通过对九宫格和1-9九个数归类分析的方法，巧妙地解决了这一经典问题，解题思路运用到的都是简单的数学逻辑关系，适合低年级学生的学习。

关键词：九宫格问题;归类分析;低年级

九宫格问题源远流长，其实质属于数独问题。笔者的孩子今年上小学一年级，近期在辅导孩子作业时又碰到这一经典问题。孩子数学老师给的解答方法虽然巧妙，但是不能给出解题的内在逻辑，因此孩子并不能真正理解而只能背答案。笔者通过查阅文献找到了两篇关于九宫格问题的解答文献，分别是《利用不定方程求解九宫格填数问题》和《九宫格问题的探讨》。[1-2]不过这两篇文献采用的解答方法涉及到未知数、甚至不定方程等高级的数学知识，涉及到比较多的抽象思维理解，因此都不适合低年级的学生。笔者虽然不是数学专业出身，但是对数学一直非常感兴趣。因此，笔者试着自行对该问题进行解答，通过努力最终找到了一种适合低年级学生的巧妙解决办法，下面将该解答方法详述如下，供大家参考。

一、问题重述

请把1、2、3、4、5、6、7、8、9 这九个数填入九宫格中，使得九宫格中每一横行、竖行、斜行的三个数之和都等于15。

二、解题思路

笔者的解题思路可以分为以下四个部分：

（1）九宫格归类分析。（2）1-9九个数归类分析。（3）数字和表格按类匹配。（4）数字归位。

其实九宫格中需要填入的数非常简单，都是10以内的数，加法也都是20以内的，小学一年级上学期就完全可以胜任了。然而难的是每一个格子或每个数相互区别又相互联系，可以说牵一发而动全身。为了把问题简化：笔者首先将九个格子和九个数先进行归类分析，这是本解题思路的核心;分类之后的格子和数就可以进行按类匹配了;最后再通过简单的尝试就可以一一归位了。

三、解题

（一）九宫格归类分析

1.格子归类

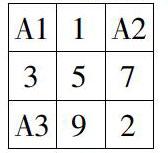
玩过三阶魔方的人都知道，九宫格很像三阶魔方中的一个面。仔细观察不难发现，这九个格子可以分为三类：角块、棱块和中心块。其中角块有4块，棱块也有4块，中心块有1块。为了方便叙述我们把角块分别标记为A1、A2、A3和A4，棱块分别标记为B1、B2、B3和B4，中心块标记为C（如下图所示）。

2.角块、棱块和中心块的分析

九宫格分为三类后，我们再来分析这三类表格在参与计算时的区别。不难发现角块、棱块和中心块参与计算的次数是有差异的，分述如下：A.角块。我们以A1角块为例，这一块需要参与到横行（A1、B1、A2），竖行（A1、B2、A3）和斜行（A1、C、A4）这三行的计算中，其他角块也是类似的，因此每一个角块参与了三次计算。B.棱块。我们以B1为例，这一块需要参与到横行（A1、B1、A2）和竖行（B1、C、B4）这两行的计算中，其他棱块也是类似的，因此每一个棱块参与了两次计算。C.中心块。中心块只有一块C，这一块需要参与到横行（B2、C、B3），竖行（B1、C、B4），斜行（A1、C、A4）和斜行（A2、C、A3）这四行的计算中，因此中心块参与了四次計算。

3.分析结论

九宫格中九个格子分为三类：1）4个角块，每个角块参与三次计算;2）4个棱块，每个棱块参与两次计算;3）1个中心块，参与四次计算。

（二）1-9九个数归类分析

尽管前面我们提到每个格子和每个数相互区别又相互联系，牵一发而动全身，让人解答起来很复杂。然而所有的数字不过9个，而且都非常简单。我们不妨倒过来去思考，可以先通过枚举法列举出所有三个数字和为15的组合来，然后将这些组合再加以分类研究。笔者就是这么做的，为了更好理解，笔者这里按照参与数字1-9的顺序进行了列举，结果见下表。

仔细观察上表我们不难发现，这九个数其实也可以分为三类：1）参与了两次计算的数，分别为1、3、7和9;2）参与了三次计算的数，分别为2、4、6和8;3）参与了四次计算的数为5。

（三）数字和表格按类匹配

九宫格分析我们发现——九个格子可以分为三类：4个角块，每个角块计算三次;4个棱块，每个棱块计算两次;一个中心块，计算四次。九个数字分析我们发现——九个数也可以分为三类：参与两次计算的数有4个，分别为1、3、7和9;参与三次计算的数有4个，分别为2、4、6和8;参与四次计算的数为5。经过简单的对照我们不难发现，表格的分类和数字的分类完全类似且一一对应。我们就可以将表格和数字进行按类匹配了：经过四次计算的数5就是中心块的数，经过两次计算的数（1、3、7和9）就是棱块的数，经过三次计算的数（2、4、6和8）就是角块的数。

（四）数字归位

经过第3步，我们已经将九宫格三类格子和三类数字做了按类匹配，接下来就可以动手填表格了。

（1）填中心块5。在第3步中已经确认中心块是5，因此将5填入中心块C。

（2）填棱块（1、3、7和9）。采用尝试法进行棱块的填写，笔者这里选择1（其他数字也是类似的）。由于迄今为止目标棱块一个都没有填，因此四个棱块其实是一样的，笔者这里把1填入棱块B1。

填完1之后，可以通过简单的计算得出B4块应该填9。

填完1和9两个数之后，棱块还剩B2和B3，属于棱块的数剩下3和7。笔者这里选择3进行下一步的填写（选7也是类似的）。由于剩余的两个棱块是对称的，因此将3填入B2还是B3是没有区别的，笔者这里就将3填到棱块B2。

填完3之后，剩下B3就只能填剩下的7了。

至此棱块就填完了。

（3）填角块（2、4、6和8）。填完棱块继续填角块，依然可以采用尝试法进行。这里笔者选择2进行尝试（其他数字也是类似的）。2的目标位置有4个，分别是A1、A2、A3和A4，由于中心块和棱块都已经填好，因此四个角块都不一样了，笔者这里尝试将2填入A1（其他尝试稍有差别，但都是类似的）。

将2填入A1后，我们把第一行（A1、B1、A2）经过简单的计算，就可以推出A2应该等于12。我们知道12并不在我们要填的剩下三个数中。因此2填A1是不成立的，同样的原因2也不能填A2。

将2填入A1后，我们把第一列（A1、B2、A3）经过简单的计算，就可以推出A3应该等于10。我们知道10同样不在我们要填的剩下三个数中。因此也可以证明2填A1是不成立的，同样的原因2也不能填A3。

因此经过这一次尝试事实上排除了2填入A1、A2和A3这三个角块的可能性，所以2只能填入A4中。

将2填入A4中后，剩下三个角块经过简单的计算就可以一一归位了，这里就不一一赘述了。

至此九宫格问题得到解决。

四、总结

本九宫格解题思路由于只涉及到低年级的数学知识，因此非常适合给低年级的学生讲解。事实上笔者的这一解题思路也是在辅导一年级孩子作业实践中得来的。尽管这一解题办法相对步骤较多，但是该方法克服了一般巧解方法中无法理解的缺陷。学生通过该解题思路一方面可以更好地理解九宫格的内在规律，另一方面可以训练低年级学生的逻辑思维能力，可以说是一举两得。文中涉及角块、棱块、中心块符号在实际给孩子讲解时可以用三种颜色进行替代，这样学生会更容易理解。

参考文献：

[1]郭柏寿.利用不定方程求解九宫格填数问题.数学学习与研究，2015，（19），90.

[2]赵立旺，胡冰瑶，汪勤.九宫格问题的探讨.数学学习与研究，2012，（01），115.