基于MEEMD和GRNN的轨道交通列车辅助逆变器故障诊断
2019-12-05盖宏宇高军伟种兴静
盖宏宇,高军伟,种兴静
(青岛大学 自动化学院,青岛 266071)
0 引言
辅助逆变器是轨道交通列车辅助系统的核心部分,其主要功能是为车辆上的低压设备提供不同的电压和不同的功率,为空调系统、车门系统、照明系统等列车电气设备(牵引除外)供电[1,2]。辅助逆变器故障会直接影响列车的正常运行,甚至是威胁到乘客的人身安全。因此,为了保证列车安全高效的运行,需要对辅助逆变器进行快速准确的故障诊断。解决此类问题的关键是提取到合适的故障信号特征。Wu等[3,4]通过研究白噪声信号的统计特征,提出了集总平均经验模式分解(Ensemble Empirical Mode Decomposition,EEMD),EEMD通过对原始信号多次加入不同的白噪声进行EMD分解,将多次分解的结果进行平均即得到最终的IMF分量。EEMD方法能很好的适用于非线性和非平稳信号的检测,在很大程度上抑制了EMD分解的模态混叠问题,但缺陷是运算量大。针对这一问题文献[5]提出了改进的集总平均经验模式分解方法(MEEMD)。MEEMD方法能够抑制待检测信号中的白噪声残余,从而使最终的IMF分量更标准。GRNN网络相对于BP网络有更好的逼近能力,训练速度更快,避免了预测结果不稳定的缺点[6]。由于上述的优点,本文采用MEEMD方法对待检测信号进行分解,将得到的具有故障信号特征的数据作为GRNN神经网络模型的输入,对列车辅助逆变器的故障信号进行故障诊断。
1 MEEMD方法理论
1.1 EMD方法基本理论
经验模态分解法(EMD)是一种时频分析方法,具有很好的自适应性和很高的性躁比,能够根据信号的时间尺度特性将非平稳、非线性的复杂信号分解成一系列稳态和线性的固有模态函数之和[7]。N.E.Huang等人[8]提出的固有模态函数必须符合两个条件:1)函数在整个时间范围内,局部极值点和过零点要交替出现,且数目必须相等或者最多相差一个;2)在任何时间点上,上下包络线的平均值必须为零,即上下包络线要关于时间轴对称。EMD分解过程可用式(1)表示为:
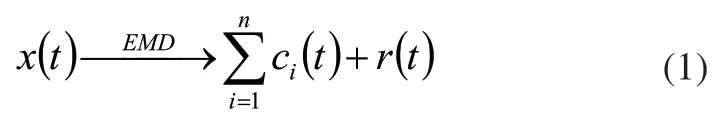
其中,ci(t)表示IMF分量;r(t)表示残余分量。
由于固有模态函数的第二个条件在实际处理中很难满足,所以Huang提出了一种迭代停止准则,规定了限制标准差[9](也称筛选门限值)为:
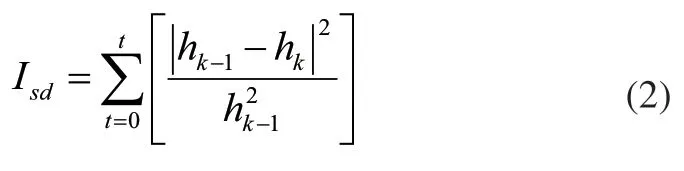
其中,t表示时间信号长度;Isd值建议取0.2~0.3,当上式所求值小于筛选门限值时,迭代将会结束[10]。
这种分解方法在实际使用中会产生模态混淆的问题。模态混淆主要是指,在同一个IMF分量中出现了不同频率的信号,或者同一频率的信号被分解到多个不同的IMF分量当中[11]。这一问题对分解的准确性产生了严重影响。
1.2 EEMD的基本理论
为了解决EMD分解方法的模态混淆问题,在原始信号中添加一定幅值的高斯白噪声,提高了信号的连续性,在对信号进行n次EMD分解,消除添加噪声对信号分解的影响。分解的具体过程如下[12]:
1)在原始信号中加入幅值标准差为常数、均值为零的高斯白噪声;
2)对含有噪声的信号进行EMD分解,得到一组IMF分量;
3)重复上述步骤n次;
4)计算得到的各IMF分量的均值,得到分解结果为:
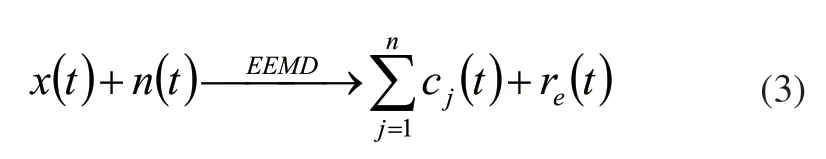
其中,re(t)表示残余分量。
EEMD方法虽然对抑制模态混叠现象有一定的作用,但对添加的白噪声的幅值有很大的要求,幅值过小,则抑制效果不明显,幅值过大,又会增加运行时间,使分解结果种产生伪分量[13]。
1.3 MEEMD方法理论
为了更好地解决EMD分解模态混叠现象,同时减少EEMD分解中的残余分量,在此基础上提出了MEEMD分解,该分解方法即保留了EEMD分解的优点,又能消除伪分量对分解结果的影响。其分解步骤如下[14]:
1)在原始信号s(t)中添加均值为零的成对白噪声信号ni(t)和-ni(t),即:

上式中,ai表示添加白噪声信号的幅值,i=1,2,…,Ne,Ne为添加白噪声对数;表示分解得到的IMF分量。
2)集成平均上述得到的分量:

其中,N表示进行EMD分解的次数,N=1,2,…,n。检测Ik(t)是否是异常信号,如果信号的熵值大于θ0,则认为是异常信号;否则近似认为是平稳信号。这里的θ0取0.55~0.6。如果Ik(t)是异常信号,则继续执行步骤1),直至IMF分量Ik(t)不是异常信号,并记为ck(t)。
3)将已经分解的前k-1个IMF分量从原始信号中分离出来,得到剩余信号r(t):

其中k=2,3,…,N。
4)MEEMD分解过程最终可以表示为:
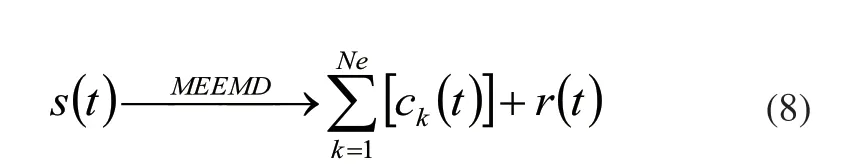
其中ck(t)表示分解得到的第k个标准IMF分量;r(t)表示最终残余分量。
2 GRNN神经网络理论
2.1 GRNN网络的基本理论
广义回归神经网络(general regression neural network,GRNN)是径向基网络的一种变形形式[15],它具有径向基神经网络的基础,有良好的非线性逼近性能,因此适用于处理非线性问题。该算法具有训练速度快、逼近能力强、仿真精度高等优点。GRNN以样本数据为后验条件,应用Parzen非参数估计,可由样本数据集按下式[15]估算密度函数f(x0,y):

其中,n表示样本容量,p表示随机变量x的维数。θ称平滑因子,它等于高斯函数的标准差。交换积分和求和顺序得:


上式中的分子为所有训练样本算得的yi值的加权和,权值为e-d(x0,xi)。
2.2 GRNN网络的结构
GRNN神经网络的创建需要将所有的数据划分为输入向量、输出向量、训练数据和测试数据,包括四层分别为:输入层、隐含层、求和层和输出层[16]。网络结构图如图1所示。
1)输入层接收样本的输入,其传输函数是简单的线性函数,神经元的个数与输入向量的维数相等,信号由输入层的输入向量传递到隐含层。
2)隐含层也称径向基层,其传输函数一般采用高斯函数,神经元个数与训练样本数相等,隐含层的径向基网络是一种性能良好的前向网络,具有最佳逼近性能。假设输入的第k个样本为xk,样本数量为K,则隐含层每一个神经元对应一个期望输出yk。
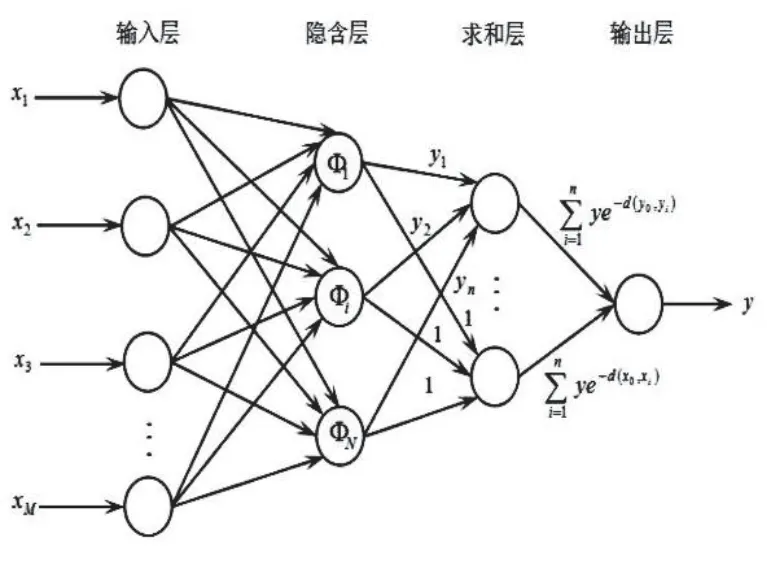
图1 广义回归神经网络结构图
3)求和层有两种神经元,第一种是分母单元,用来计算隐含层神经元的代数和;第二种是分子单元,用来计算隐含层神经元的加权和,权值为训练样本的期望输出值。如图1所示,求和层分子单元的输出值y1等于隐含层输出值乘以yk后的和,分母单元的输出值y2等于隐含层输出值直接求和。
4)输出层是线性层。由图1可知输出的估算值y=分子单元的输出值y1/分母单元的输出值y2。
3 仿真实验
列车辅助逆变器的故障有很多种,本文选取轨道交通列车常见的三种故障信号:电压骤降、频率变换和脉冲暂态,进行仿真实验。每种故障选取22组训练样本和10组测试样本共32组样本数据。首先对样本数据提取故障特征向量,本文采用MEEMD方法分解原始信号,得到IMF分量和残余分量,其中电压波动的IMF分量及残余分量如图2所示。

图2 电压波动原始信号及IMF分量
辅助逆变器的典型故障信息主要集中在频率比较高的分量中,由图2可以看出,频率较大的分量是从IMF1分量到IMF5分量,因此本文选取每组分解结果中的前5个IMF分量组成的数据作为GRNN网络的输入数据。采用MEEMD分解方法提取到的部分故障特征向量如表1所示。
本文将分解得到的故障特征向量作为GRNN神经网络的输入向量,频率变换、脉冲暂态和电压波动对应的期望输出分别为1,2和3。利用MATLAB建立GRNN网络模型,由输入层、隐含层、求和层和输出层组成,广义回归神经网络不需要训练,本文中的SPREAD值为0.6。采用广义回归神经网络进行的故障检测部分结果如表2所示。
如表中所示,本文每种故障有12组测试样本,GRNN神经网络在这36个测试样本中有35个诊断正确,准确率为97.2%,高于BP神经网络77.0%的准确率。因此,本文采用的MEEMD分解方法结合GRNN神经网络模型的算法,能够实现对辅助逆变器故障的诊断,并且满足列车辅助逆变器故障诊断对准确率的要求。
4 结语
本文结合MEEMD方法,建立了广义回归神经网络模型对列车辅助逆变器进行故障诊断,并于BP神经网络模型进行对比。通过MEEMD方法对原始故障信号进行分解,得到了多个原始故障信号的IMF分量,并将其输入到所建立的GRNN神经网络模型中进行故障诊断。MEEMD方法避免了原EEMD方法中不必要的集成平均,有效的克服了传统信号特征向量提取方法中模态混淆的不足,GRNN神经网络模型结构简单,需要人为调节的参数少,有效避免了人为因素对结果的影响。从仿真实验结果可以看出,该算法将MEEMD方法与GRNN神经网络模型相结合使故障诊断的准确率更高,满足了对列车辅助逆变器故障诊断结果的要求。
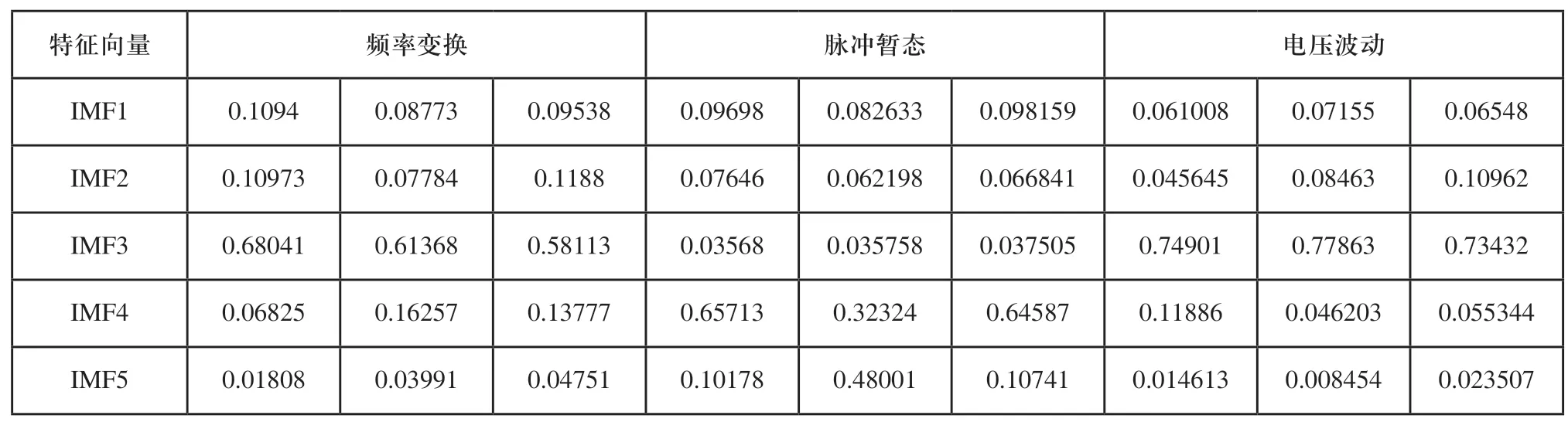
表1 MEEMD方法提取特征向量的部分结果

表2 测试样本故障检测的部分结果
