点、直线、平面之间的位置关系综合演练B 卷

■刘中亮

一、选择题

1.对于空间中的两条直线m,n和一个平面α,下列命题中的真命题是( )。

A.若m∥α,n∥α,则m∥n

B.若m∥α,n⊂α,则m∥n

C.若m∥α,n⊥α,则m∥n

D.若m⊥α,n⊥α,则m∥n

2.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )。

A.若m∥α,n∥α,则m∥n

B.若α⊥γ,β⊥γ,则α∥β

C.若m∥α,n∥β,m∥n,则α∥β

D.若m⊥α,n⊥α,则m∥n

3.已知m,n是空间中两条不同的直线,α,β是两个不同的平面,现有以下结论:①m⊂α,n⊂β,m⊥n⇒α⊥β;②m∥β,n∥β,m⊂α,n⊂α⇒α∥β;③m⊥β,n⊥α,m⊥n⇒α⊥β;④m⊂α,m∥n⇒n∥α。

其中正确结论的个数是( )。

A.0 B.1

C.2 D.3

4.下列命题中,正确的是( )。

A.存在两条异面直线同时平行于同一个平面

B.若一个平面内两条直线与另一个平面平行,则这两个平面平行

C.底面是矩形的四棱柱是长方体

D.棱台的侧面都是等腰梯形

5.在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则( )。

A.MN∥C1D1

B.MN⊥BC1

C.MN⊥平面ACD1

D.MN⊥平面ACC1

6.已知一个平面α,对于空间内的任意一条直线a,在平面α内一定存在一条直线b,使得a与b( )。

A.平行 B.相交

C.异面 D.垂直

7.如 图1 所 示,在 正 方 体ABCDA1B1C1D1中,点P在 线 段AD1上 运 动,则异面直线CP与BA1所成角的取值范围是( )。

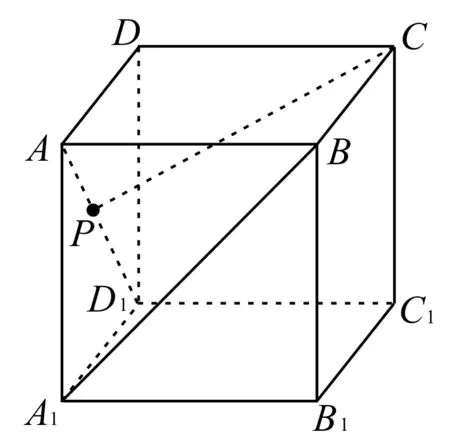
图1

8.已知m,n是 两 条 不 同 的 直 线,α,β是两个不同的平面,若m⊥α,n⊥β,且β⊥α,则下列结论一定正确的是( )。

A.m⊥nB.m∥n

C.m与n相交 D.m与n异面

9.已知平面α及直线a,b,则下列说法正确的是( )。

A.若直线a,b与平面α所成角都是30°,则这两条直线平行

B.若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直

C.若直线a,b平行,则这两条直线中至少有一条与平面α平行

D.若直线a,b垂直,则这两条直线与平面α不可能都垂直

10.已知m,n是空间中两条不同的直线,α,β为空间中两个互相垂直的平面,则下列命题正确的是( )。

A.若m⊂α,则m⊥β

B.若m⊂α,n⊂β,则m⊥n

C.若m⊄α,m⊥β,则m∥α

D.若α∩β=m,n⊥m,则n⊥α

11.若直线l与平面α相交,则( )。

A.平面α内存在直线与l异面

B.平面α内存在唯一的直线与l平行

C.平面α内存在唯一的直线与l垂直

D.平面α内的直线与l都相交

12.已知l,m,n为三条不同直线,α,β,γ为三个不同平面,则下列判断正确的是( )。

A.若m∥α,n∥α,则m∥n

B.若m⊥α,n∥β,α⊥β,则m⊥n

C.若α∩β=l,m∥α,m∥β,则m∥l

D.若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α

13.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )。

A.若α⊥β,m⊂α,n⊂β,则m⊥n

B.若α∥β,m⊂α,n⊂β,则m∥n

C.若m⊥n,m⊂α,n⊂β,则α⊥β

D.若m⊥α,m∥n,n∥β,则α⊥β

14.设a,b,c是空间的三条直线,现有以下命题:①若a⊥b,b⊥c,则a⊥c;②若a,b是异面直线,b,c是异面直线,则a,c也是异面直线;③若直线a与b相交,直线b与c相交,则直线a与c也相交;④若a与b共面,b与c共面,则a与c也共面;⑤若a∥b,b∥c,则a∥c。

其中正确的命题个数是( )。

A.0 B.1

C.2 D.3

15.如图2,以等腰直角三角形ABC的斜边BC上的中线AD为折痕,将△ABD与△ACD折成互相垂直的两个平面,得到以下四个结论:①BD⊥平面ACD;②△ABC为等边三角形;③平面ADC⊥平面ABC;④点D在平面ABC内的射影为△ABC的外接圆的圆心。

图2

其中正确结论的序号是( )。

A.①②③ B.②③④

C.①②④ D.①③④

16.如图3,在正方体ABCD-A1B1C1D1上有一只蚂蚁从A点出发沿正方体的棱前进,若它走进的第n+2条棱与第n条棱是异面的,则这只蚂蚁走过第2016条棱之后的位置可能在( )。

图3

A.点A1处 B.点A处

C.点D处 D.点B1处

二、填空题

17.若直线l⊥平面β,平面α⊥平面β,则直线l与平面α的位置关系为_____。

18.设m,n是 两 条 不 同 的 直 线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊂α,n∥α,则m∥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;③若α∩β=n,m∥n,m∥α,则m∥β;④若m∥α,n∥β,m∥n,则α∥β。

其中正确的命题是_____。(填序号)

19.已知直线m,l,平面α,β,且m⊥α,l⊂β,给出下列命题:①若α∥β,则m⊥l;②若α⊥β,则m∥l;③若m⊥l,则α⊥β;④若m∥l,则α⊥β。

其中正确命题的序号是____。

20.若m,n表示不重合的两条直线,α表示平面,给出下列命题:①若m∥n,m⊥α,则n⊥α;②若m⊥α,n⊥α,则m∥n;③若m∥n,n⊂α,则m∥α;④若m,n与α所成的角都为60°,则m∥n。

其中正确命题的序号是____。

21.如图4,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=。

图4

22.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则__

(写出所有正确结论的编号)。

①四面体ABCD每组对棱相互垂直;

②四面体ABCD每个面的面积相等;

③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;

④连接四面体ABCD每组对棱中点的线段相互垂直平分;

⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长。

23.如图5 所示,已知正方体ABCDA1B1C1D1。

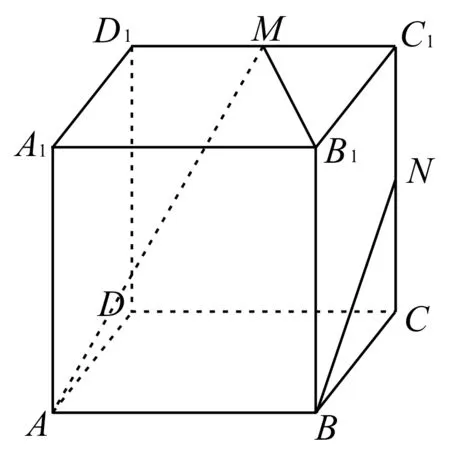
图5

M,N分别为棱C1D1,C1C的中点,现有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线。

其中正确结论的序号是____。

24.如图6,已知四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,点E,F分别是棱PC,PD的中点。

图6

现有下列结论:①CD∥平面AEF;②直线BF与直线AE为异面直线;③△PDC的面积与△PAD的面积一定不相等;④四棱锥P-ABCD外接球的球心一定是点E。

其中正确的结论是____。(写出所有正确结论的编号)

25.如图7,在正方体ABCD-A1B1C1D1中,点M,N分别是棱A1D1,AA1的中点。

图7

现有下列几种说法:①C1M∥AC;②BD1⊥AC;③BC1与AC所成的角为60°;④B1A1,C1M,BN三条直线交于一点。

其中正确的说法是____。(写出所有正确说法的编号)

三、解答题

26.如图8,在四面体ABCD中,E,H分别是线段AB,AD的中点,F,G分别是线段CB,CD上的点,且

图8

求证:(1)四边形EFGH是梯形。

(2)AC,EF,GH三条直线相交于同一点。

27.如图9,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点。

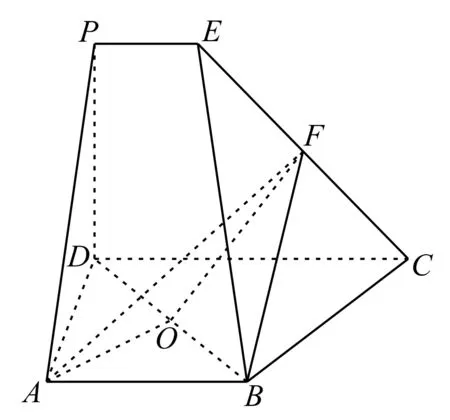
图9

(1)求证:BF∥平面ADP。

(2)已知O是BD的中点,求证:BD⊥平面AOF。

28.如图10,侧棱与底面垂直的四棱柱ABCD-A1B1C1D1的 底 面 是 梯 形,AB∥CD,AB⊥AD,AA1=4,DC=2AB,AB=AD=3,点M在棱A1B1上,且A1M=A1B1。点E是棱CD上的一点,AM∥平面BC1E。

图10

(1)试确定点E的位置,并说明理由。

(2)求三棱锥M-BC1E的体积。

29.如图11,在四棱锥P-ABCD中,底面ABCD是 边 长 为1 的 正 方 形,PC⊥底 面ABCD,且PC=2,E是侧棱PC上的动点。

图11

(1)求四棱锥P-ABCD的表面积。

(2)在棱PC上是否存在一点E,使得AP∥平面BDE? 若存在,指出点E的位置,并证明;若不存在,请说明理由。

30.如图12,在四面体ABCD中,AC=6,BA=BC=5,AD=CD=

图12

(1)求证:AC⊥BD。

(2)当四面体ABCD的体积最大时,求点A到平面BCD的距离。

31.如图13,已 知 梯 形ABCD中,AD∥BC,∠ABC= ∠BAD=,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图14)。G是BC的中点,以F,B,C,D为顶点的三棱锥的体积记为f(x)。

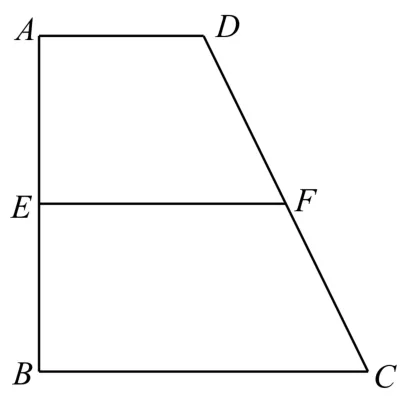
图13

图14

(1)当x=2时,求证:BD⊥EG。

(2)求f(x)的最大值。

(3)当f(x)取得最大值时,求异面直线AE与BD所成角的余弦值。