与圆有关的最值问题的求解策略

■何 芳

直线与圆的关系中存在一些最值问题,如距离的最值、面积的最值等。这类问题可利用数形结合法求解。 下面分类解析。

一、与距离有关的最值问题

例1直线y-3=k(x-1)被圆C:(x-2)2+(y-2)2=5所截得的最短弦长等于____。

解：易知直线过定点,且定点在圆内,当圆被直线截得的弦最短时,圆心到弦的距离最大,此时圆心与定点的连线垂直于弦。

由圆C:(x-2)2+(y-2)2=5,可知圆心C(2,2),半径为5。直线y-3=k(x-1)恒过定点(1,3),当圆被直线截得的弦最短时,圆心C(2,2)与定点P(1,3)的连线垂直于弦,这时弦心距为。故所截得的最短弦长为

评析：本题主要考查直线与圆相交的性质。过圆内一点的最长弦为圆的直径,最短弦是以该点为中点的弦。

二、圆的面积的最值问题

例2在平面直角坐标系xOy中,圆C与圆O:x2+y2=1 相外切,且与直线x-2y+5=0 相切,则圆C的面积的最小值为____。

解：画出图形,求出最小圆的半径,即得圆的面积。如图1,圆心O到直线的距离

图1

由图1可知,所求圆的半径r。故圆C面积的最小值为

评析：本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法。过两定点的所有圆中,面积最小的是以这两个定点为直径端点的圆的面积。

三、直线斜率的最值问题

例3若直线y=k(x-2)与曲线有公共点,则k的最小值为( )。

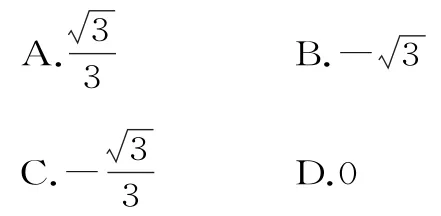
解：直线y=k(x-2)过定点(2,0),作出曲线y=(y≥0)与直线y=k(x-2)的图像,如图2所示。

图2

由y=k(x-2),可得kx-y-2k=0。由直线与圆(半圆)相切可得,解得。所以当直线y=k(x-2)与曲线有公共点时,k的最小值为。应选C。

评析：本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法。需要注意的是题中的曲线是半圆,当直线与圆相切时斜率取得最值。