运载火箭返回着陆在线轨迹规划技术发展

宋征宇，王 聪

(1.中国运载火箭技术研究院，北京 100076;2.北京航天自动控制研究所, 北京 100854)

0 引言

在人类航天和空间探索事业发展过程中，航天发射和运输系统的高风险、高成本和高复杂性一直是难以逾越的瓶颈，回收火箭并多次使用是能够降低发射成本的重要途径之一，也是未来地外天体定点软着陆以及垂直起降大范围机动的关键技术之一。然而，火箭返回垂直着陆充满挑战。由于火箭返回过程中飞行空域跨度大、飞行环境变化显著、过程约束复杂，经历了由稀薄大气层边缘经稠密大气到地面着陆的过程，面临一系列不确定性。传统的基于离线规划、在线跟踪的方式无论从可靠性、适应性、最优性等角度，均已无法满足大范围、多阶段、高动态和多约束的应用环境与要求。在线轨迹规划技术能够根据火箭当前状态在线生成满足约束条件的飞行轨迹，使其在返回着陆过程中具备自适应调整和在线实时优化能力，能够有效应对各种干扰和突发情况，是实现可重复使用火箭垂直着陆的关键技术。国内外的研究普遍表明，仅从着陆段的制导与控制技术看(不考虑前序飞行段的导航等因素)，在月球、火星和地球上实现定点软着陆(pinpoint landing)的技术难度逐步递增。因此，实现运载火箭垂直着陆的意义，早已超过仅仅火箭重复使用这一个需求。

本文主要总结国外针对垂直着陆以及再入返回着陆在线轨迹规划技术所开展的理论、算法研究及工程进展。

1 在线轨迹规划技术的发展

1.1 最优控制

运载火箭回收的概念及回收方式早在20世纪90年代就已被提出[1-2]，但直到2015年年底人类才第一次成功回收运载火箭。考虑到着陆过程存在的大量不确定性，研究人员和任务设计者一直在追求在线生成可行或者最优轨迹的能力[3]，前提是满足飞行过程的边界条件、路径约束以及标称运动方程。基于在线轨迹优化方法解决制导问题也是航天控制领域的研究热点[4]。针对着陆过程的大部分传统闭环制导方法主要将问题转换为仅具有终端约束的最优反馈控制问题(没有路径约束)，利用庞特里亚金极大值原理或变分法进行求解[5-6]，这类制导律称为最优制导律[7]。由于存在强不确定性，最优制导律加入了基于滑模控制理论的非线性项，可以在不准确测量和未建模动态的情况下提高其鲁棒性[8]。由于可以增强鲁棒性，这个研究方向在过去几年中得到了发展并应用于不同的场景[9-10]。

1.2 多项式制导

当飞行任务必须满足更严格的约束要求时，通常需要求解具有终端和路径约束的轨迹规划问题，例如高着陆精度或人员安全性(载人任务)。这类方法始于Apollo计划，并被继续使用于火星着陆器，也可以在地球上被用于垂直起降[7]。上述问题通常是非线性的且求解困难，直到过去10年仍只能离线求解。为了简化问题，Apollo登月舱的加速度设计为关于时间的二次多项式[11]。这样生成的轨迹并不是最优的，因为没有对性能指标进行优化；但是二次多项式的系数可以通过预定下降时间的终端边界条件进行解析求解。这种方法在NASA的火星科学实验室(Mars Science Laboratory, MSL)探测器中进行了修改，增加了对动力下降段持续时间的线性搜索，来最小化燃料消耗[12-13]。除了这些扩展之外，还可以通过增加开环制导律的多项式阶数使系数计算欠定，提供系数选择的优化空间。但是，这些制导方式的落点偏差均在千米级以上，远没有实现定点着陆。

1.3 计算制导

随着硬件平台计算能力的不断提升，为了进一步提升航空航天器制导的自主性，近几年计算制导这个新的研究方向越来越得到关注[14-15]。相比传统的航天器制导方法，计算制导强调用优化迭代计算来逐步取代传统的解析制导律，依靠鲁棒高效的优化计算方法和先进的硬件计算平台，来处理航天领域中针对复杂非线性动态系统的优化计算难题，突破传统制导方法的瓶颈[14]。处理复杂非线性动态系统能力的增强，可以进一步提升航天器制导性能，使航天器更加智能自主，对复杂多样的任务具有更好的适应性。Bollino等[16-17]基于直接法中的伪谱方法和采样反馈技术提出了滚动时域在线轨迹优化制导框架，并应用于航天器再入制导。Seebinder等[18]引入灵敏度理论进行在线轨迹生成，基于非线性规划参数灵敏度分析和离线优化的轨迹来在线生成近似最优轨迹，并应用于火星大气进入在线轨迹生成问题。Sagliano等[19]将多变量伪谱插值方法与子空间选择算法相结合，基于离线最优轨迹数据库在线生成近似最优参考轨迹，应用于再入飞行器在线参考轨迹生成问题。

1.4 凸优化

在计算制导研究中，基于凸优化的在线轨迹优化方法成为了研究热点并得到快速发展。凸优化的特征[20]如表1所示。

表1 凸优化特征

采用凸优化方法进行优化计算，需要首先将问题进行凸化转换，然后采用对偶内点法进行求解。对偶内点法的求解框架如图1所示。

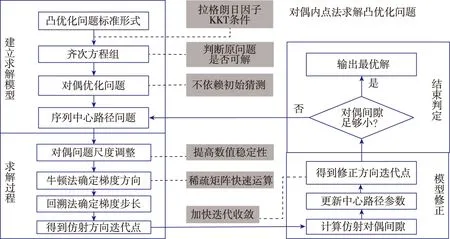
图1 对偶内点法求解框架

但是，并非所有问题均可进行无损凸化转换，因此常用的做法是序列凸优化。例如先将问题进行线性化和凸化处理，在求得当前凸优化子问题最优解后，根据解的结果重新修正优化命题，重复上述过程进行再一次求解；当前后两次求解的结果其偏差小于一定范围时，认为计算收敛停止迭代。在基于配点法的一般数值问题求解中，也会经常用到建立多个子问题进行迭代求解的方法，有时称作约束松弛方法，即通过建立简化的问题，提升求解速度；然后逐步完善至原问题，求解难度逐步加大；但前后两个问题比较相似，因此可以用前述一个问题的解作为后续问题的合理初值猜想，从而加快后续问题的求解效率。相对于这种策略，对偶内点法由于对初值不敏感而无法效仿，这也是常说对偶内点法无法“热启动”的原因。

Sagliano[31]将伪谱离散方法和凸优化相结合用于动力下降和着陆过程在线轨迹优化。如果无法将轨迹优化问题一次性转化为凸优化问题，通过序列凸优化算法将求解原问题转化为求解一系列凸优化问题来得到原问题的解[32-34]。Szmuk等[35]、Mao等[36-37]在一定前提下给出了序列凸优化算法的收敛性证明。Pinson等[38]研究了一种以燃料最省为目标，用于不规则星体着陆的凸优化方法。Wang等[39]通过定义新的状态量和控制量实现对再入运动方程状态量和控制量的解耦，利用序列线性化将原优化问题表述为一系列有限维凸问题，并研究了基于序列半正定规划的轨迹优化算法[40]。

相比于火星着陆，运载火箭地球着陆不可忽略气动力[41]，因而动力下降段的飞行优化问题非线性更强，可靠高效求解更为困难，因此研究成果还较为有限。Szmuk等[35]研究了含气动阻力的燃料最优着陆优化问题，利用连续凸化将原非凸问题转换为迭代求解凸优化子问题[42]。Liu[42]将推力与攻角(控制气动升阻力)同时作为控制量，将对应的燃料最优着陆问题转化为凸优化问题进行迭代求解，并从理论上证明了所采用松弛技术的有效性。Wang等[43]将该研究工作拓展到飞行时间自由的问题，并研究了在模型预测框架下通过凸优化得到制导指令的方法。为了提高着陆飞行轨迹的精度，Wang等[44-45]将伪谱法与凸优化相结合，提出伪谱离散-改进序列凸优化算法求解含过程约束的着陆优化问题，并基于模型预测控制与凸优化设计了着陆制导算法。张志国等[46]同样采用了凸优化，并通过在线求解凸优化问题实时得到着陆段制导指令。Ma等[47-48]采用非线性规划与伪谱法求解火箭返回全程优化问题，并提出内外增长初始化策略提高算法的收敛性。可以看出，以上研究均采用了基于序列凸优化或非线性规划的方法，但还无法从理论上保证算法的收敛性，目前仅能通过各类技巧提高算法的收敛效果，包括利用数值优化中的线性搜索方法(计算步长)或信赖域方法(动态调整信赖域半径)[49]，以及更利于序列凸优化收敛的凸化方法[50]。此外，算法的不可靠(无法保证收敛)通常也使其难以满足实时性要求。

总而言之，提高着陆轨迹优化的可靠性与计算效率仍是目前学术界的研究难点，具有重要的学术价值和潜在的应用价值。目前,国内外在该领域的研究仍处于探索阶段，现有方法还难以工程应用。深入研究保证收敛、具备在箭载计算机上实时计算、性能鲁棒的精确着陆制导方法，对助力我国早日掌握火箭回收技术，提高我国在商业航天国际发射市场中的竞争力具有非常重要的意义。

2 美国开展的实践研究

美国的定点着陆经历了月球、火星以及地球3种环境，其定点着陆的难度逐渐加大。

2.1 Apollo任务

对于月球着陆，经典的Apollo制导算法在动力下降段根据状态边界约束和固定飞行时间，寻找加速度剖面的闭合形式解。尽管Apollo任务取得了令其自身专家均感到惊讶的成果，其制导方法仍存在以下不足：1)制导生成的轨迹不能保证满足飞行器推力约束，因此在制导指令中引入散布修正项；2)除终端约束外，对飞行器状态没有约束，生成的轨迹可能会进入地下或与障碍物碰撞；3)轨迹在时间或燃油消耗方面也不是最佳的。

自Apollo计划结束以来，为了提高性能，对着陆段制导方法进行了扩展[12]。修改后的Apollo制导算法将飞行时间作为自由变量，通过对飞行时间的线性搜索，查找符合飞行器约束、着陆时间最短或燃料消耗最小的飞行轨迹。这种方法可以在不显著增加实现复杂性的情况下大大提高性能，但并不是全局最优的轨迹。

2.2 火星探测任务

对于火星着陆任务,NASA火星科学实验室MSL在2012年着陆时使用了基于Apollo的改进式多项式制导方法进行动力下降。该算法的目标是在动力下降段实现抛伞点到目标点高精度的高度和航程控制，并且多项式制导能够在飞行器匀速垂直下降之前消除水平速度，使垂直速度达到预定值。

尽管MSL的制导算法进行了改进，但其对再入初始条件的适应能力仍然有限，因此考核制导算法的性能仅针对开伞点，即将针对开伞点的控制精度和机动性能作为考核指标[51]，如果开伞点距离标称位置差距较大，制导算法并不具备在线规划和定点控制的能力，因此，火星着陆的落点偏差都在千米级以上。

2.3 未来火星定点着陆探测

NASA认为，Apollo任务及其改进算法无法满足定点着陆的要求，主要是由于机动范围受限。着陆的最后两个阶段是减速段(比如采用降落伞减速)、动力下降段(powered descent, PD)，由于减速段很难准确控制与PD段的交接班条件，因此PD段的初始状态无法提前确定，这时需要采用自主制导(autonomous guidance)来实现轨迹调整和控制，示意图如图2所示[52]。

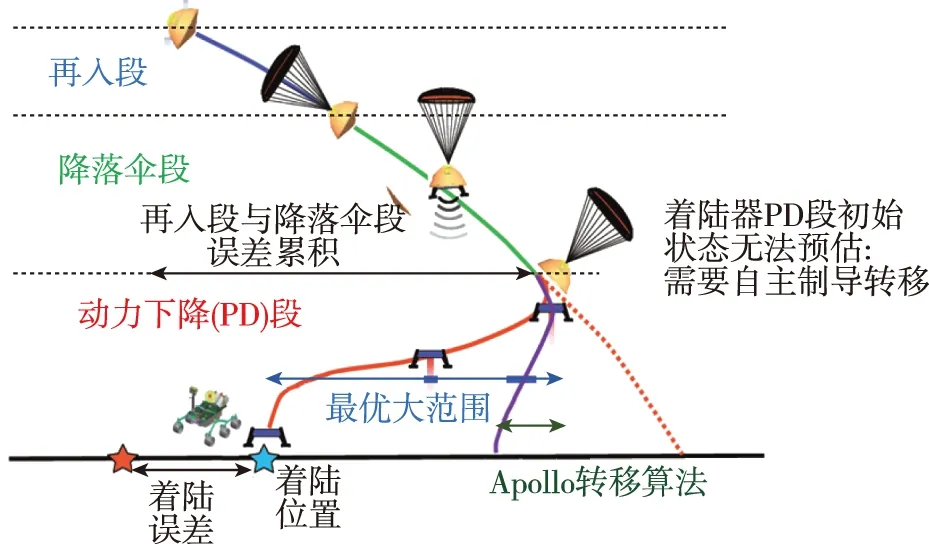
图2 自主制导示意图

迄今为止，着陆任务通常针对行星表面平坦的区域，以提高安全着陆的概率。但未来对火星探测的需求不仅局限于此，更有价值的科学兴趣点往往位于地势险峻甚至沟壑和谷底，那里可能曾经是河流冲刷的遗迹。对这些地区的探测，靠火星车从平坦处翻山越岭来考察是不现实的，因此定点着陆成了任务成功的前提条件。目前，包括NASA自主精确着陆危险规避技术(Autonomous Landing Hazard Avoidance Technology, ALHAT)[53]、美国国家航空航天局自动着陆系统(Autonomous Autolanding System, AAS)[54]、NASA JPL着陆器视觉系统(Lander Vision System, LVS)[55]在内的多种自主精确导航和危险检测技术正处于开发和测试阶段，这些系统的发展和精确着陆制导将使自主定点着陆精度控制在100m范围内，从而具备探测科学家们更感兴趣的危险区域的能力。

为此，JPL从2004年起就提出了一种燃料最优大范围转移(Guidance for Fuel-Optimal Large Diverts, G-FOLD)[52]的制导算法，历经9年的研发。该算法在节省燃料的同时，充分利用飞行器的机动能力，最大化着陆精度，并结合推力大小和方向约束，以最大速度和地表避障为状态约束，生成可行的飞行轨迹。

G-FOLD利用无损凸化方法引入附加松弛变量对优化问题进行增广，采用一组等效的控制约束凸化着陆优化问题，生成满足状态量和控制量约束的燃料最省飞行轨迹。并且设计了基于内点法算法的定制化二阶锥优化求解器SOCP(Second Order Cone Programming)，提升轨迹优化的效率和可靠性。2012年，JPL主导的自主上升与下降动力飞行试验项目(Autonomous Ascent and Descent Powered-Flight Testbed, ADAPT)[56]在Xombie飞行器上成功对G-FOLD算法进行了测试，能以每100ms在线计算一次的周期，将着陆精度控制在米级,算法框图如图3所示。

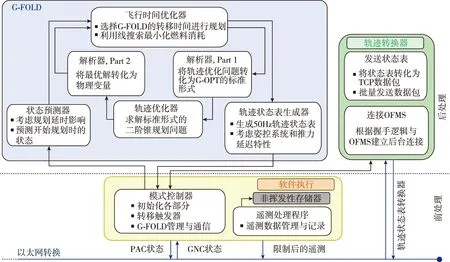
图3 G-FOLD在线轨迹规划框图

G-FOLD中包含4个主要模块，即飞行时间优化器(剩余飞行时间按照最小燃料消耗的目标进行线性搜索得到)、轨迹优化器(转换为二阶锥优化问题)、状态预测器(考虑对规划的时延进行补偿)和轨迹状态表生成器(离散精度为20ms)；以及前处理和后处理模块，其中前处理是将优化命题转换为G-OPT的标准形式，后处理是将计算结果中的一些松弛变量转换为原来的物理变量。

该技术让NASA看到了火星定点着陆的希望。2015年，在NASA最新版技术发展路线图(2015 NASA Technology Roadmaps)的第9个领域“再入、下降和着陆系统”中重点提到了大范围移动制导方法[57]，其中对G-FOLD算法评价为“NASA目前所知的唯一满足约束、燃料最优且自主的算法”，实现了在线制导。在该路线图中，NASA还总结了与其有关的技术子项，包括凸优化问题的求解、在飞行计算机上实现大范围移动的制导方法、大范围移动制导方法测试平台3部分,如表2所示。

表2 在线轨迹规划关键技术

为了验证该算法，NASA资助了多个小型飞行器的研制，并提供在这些飞行器上进行飞行验证的机会(通过NASA Flight Opportunities项目进行申请)。这些不同类型的验证飞行器如图4所示。

图4 美国各类垂直起降验证飞行器

2.4 Falcon9火箭

SpaceX公司的技术人员与前期开展凸优化研究的美国学者和研究团队有着千丝万缕的联系。在其制导/导航与控制技术GNC首席工程师Blackmore看来[41]，在地球上带有大气的再入定点着陆比火星更困难。主要原因是地球的大气密度大约是火星的100倍以上，气动力已经不能当作一项较小的干扰而被忽略。

图5[41]所示的地球着落飞行过程中，最后红色包络的阶段系采用了动力转移制导(powered divert guidance, PDG)，目的是消除前序飞行段积累的误差。从图5中可以看出，在有动力工作的阶段，如上升段、反推段，能够减小控制偏差；在大气层外滑行段，偏差基本维持不变；而在气动减速段，受大气扰动影响偏差增大，这些增大的偏差完全依靠最后的PDG制导来消除。对比图5和图2可以看出，在线轨迹规划的主要使命，就是在末端动力反推起点初始状态不能提前确定(取决于气动减速和伞降减速的控制精度)的情况下，将飞行器着陆在提前确定的终点上。

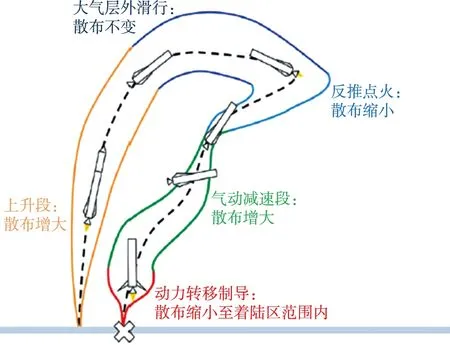
图5 SpaceX对垂直起降过程剖面的描述

Blackmore透露[41]，他们使用CVXGEN (Mattingley and Boyd 2012)生成定制化的飞行代码，从而在考虑气动力的条件下，能够实现对精确着陆段轨迹规划问题的在线快速求解。实现这一目标需要非常快速的在线凸优化，在零点几秒内得到最优飞行轨迹。

为实现火箭垂直回收，SpaceX开展了多次回收试验，制定了多元、渐进式发展的重复使用技术验证计划，其研究过程如图6所示。该计划包括以下3种试验：低空(低于3.5km)、低速测试，高空(3.5km～91km)、中速测试，高空(91km以上)、高速(Ma=6)的弹道式再入、受控减速和受控降落试验。其中前2种主要通过蚱蜢验证机、F9R-Dev和新型F9R-Dev2验证机进行验证，而第3种则结合Falcon-9火箭发射任务进行。经过持续的地面试验以及飞行试验，于2015年12月22日在陆地第一次成功回收了Falcon 9一级火箭，又于2016年4月8日在海上第一次成功回收了Falcon 9一级火箭，标志着SpaceX突破了垂直着陆技术。2018年2月6日，Falcon Heavy火箭升空，并成功同时回收了两枚助推器。

目前,国际上将火箭垂直着陆的过程分为两种形式：1)返回原场(return to site)，火箭以着陆后减少运输成本为目的，返回发射场附近；2)顺程着陆(down range landing)，火箭以尽可能减少回收损失的运载能力为目的，在飞行方向上，设置移动着陆平台。Falcon Heavy的发射任务示意图如图7所示[58]，其中两台助推器分离时刻较早采用返回原场方式回收，芯级分离时刻能量较大采用顺程着陆的方式进行回收。

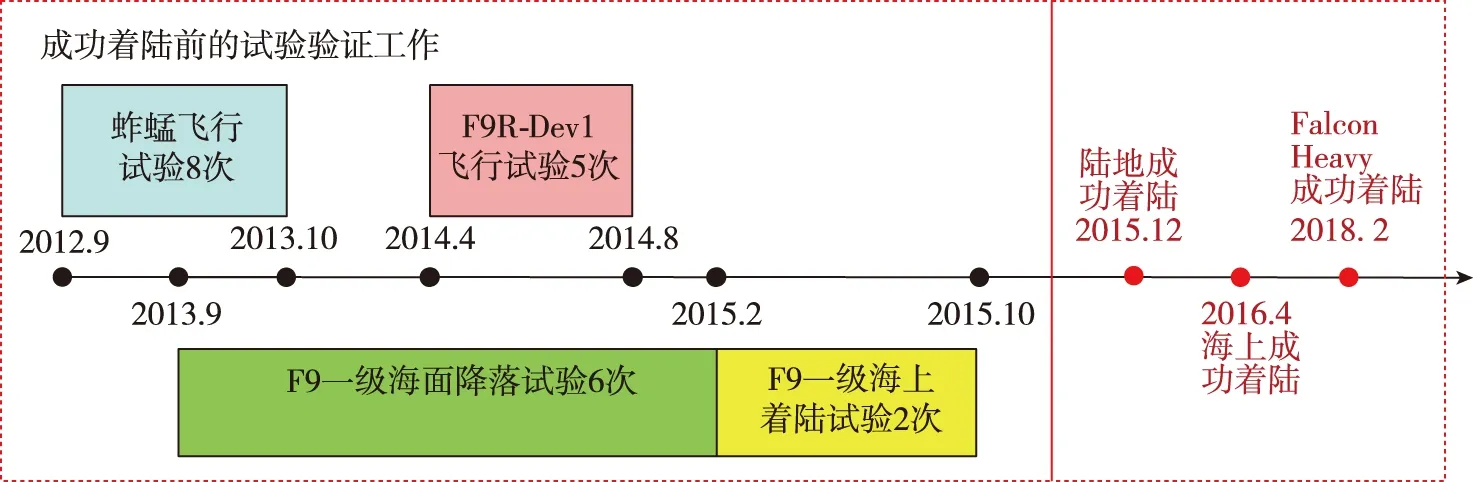
图6 SpaceX垂直着陆技术研究过程

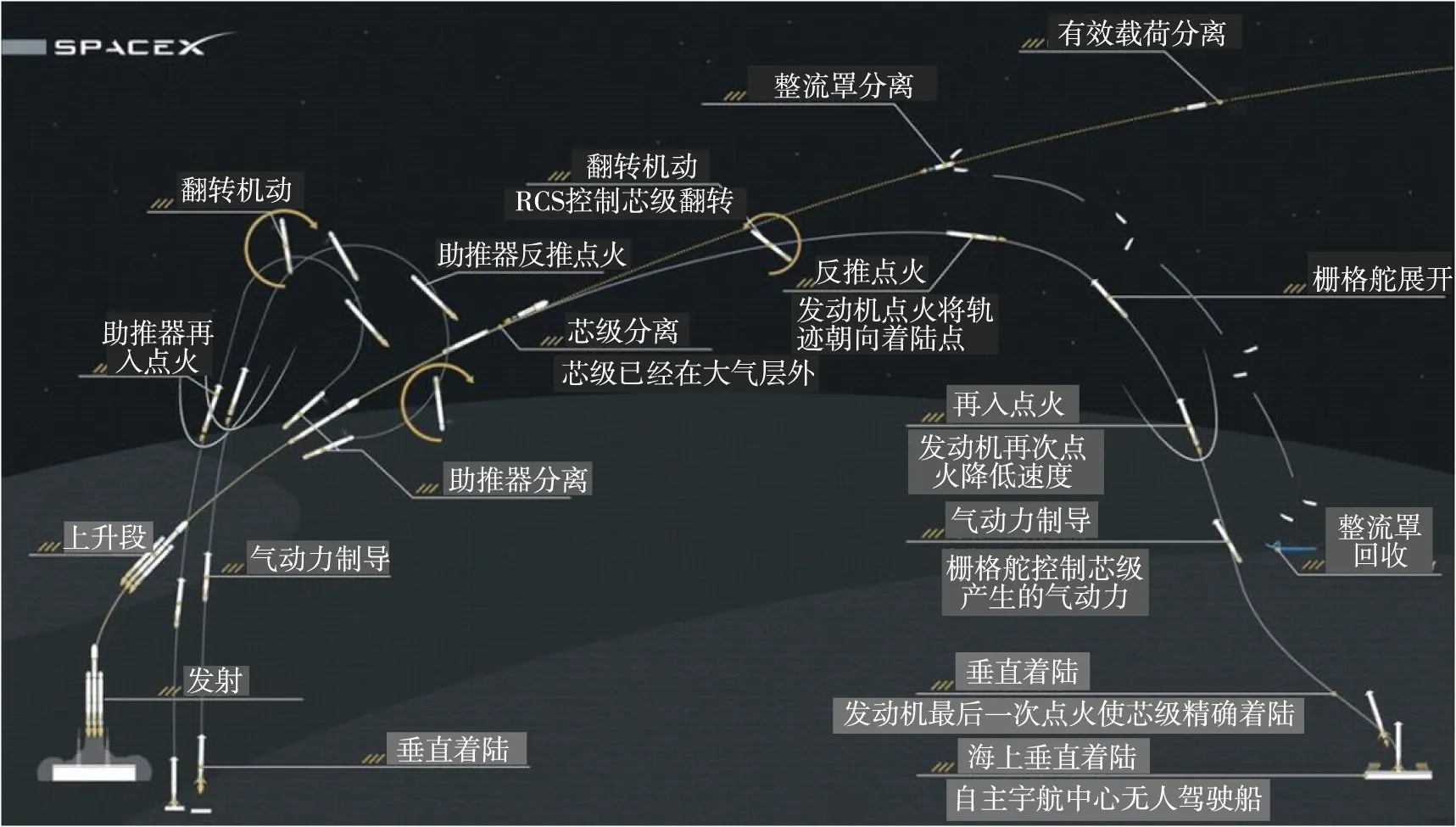
图7 Falcon Heavy发射任务示意图

3 其他国家相关工作

3.1 法国航天局(Centre National D’Etudes Spatiales, CNES)

CNES认为制导/导航与控制技术GNC是垂直着陆过程最具挑战的技术之一，并研发了分别基于涡喷发动机和挤压式火箭发动机的FROG(a Rocket for GNC demonstration)验证平台，用于验证垂直着陆过程中的制导控制算法,见图8(a)。然而从文献上看[59]，在FROG中并没有采用在线规划算法，而是离线根据直接法规划最优轨迹，并存贮在嵌入式计算机中；通过设计PID控制率和LQG最优控制率对俯仰、偏航和滚动三通道进行控制，实现对着陆轨迹的跟踪。

3.2 德国航空航天中心(Deutsches Zentrum fur Luft- und Raumfahrt, DLR)

DLR研制了EAGLE (Environment for Autonomous GNC and Landing Experiments)垂直起降验证平台[60]，并利用凸优化算法实时计算动力着陆段燃料最省的飞行轨迹,见图8(b)。根据最大可用加速度分别估计水平和竖直飞向的剩余飞行时间，取两者最大值作为预计剩余飞行时间；并通过松弛终端约束的方式避免这个估计值有可能导致找不到最优解的情况。算法采用梯形法和伪谱法对凸优化问题进行离散化，采用ECOS求解器快速计算。该求解器是苏黎世理工大学成立的Embotech公司研发的基于对偶内点法的凸优化问题嵌入式求解器，该公司还研发了基于数值算法的实时决策软件FORCES[61]，从数值优化理论上支撑欧洲各国和欧空局开展包括垂直着陆在内的在线轨迹规划研究工作。

(a)FROG

(b)EAGLE

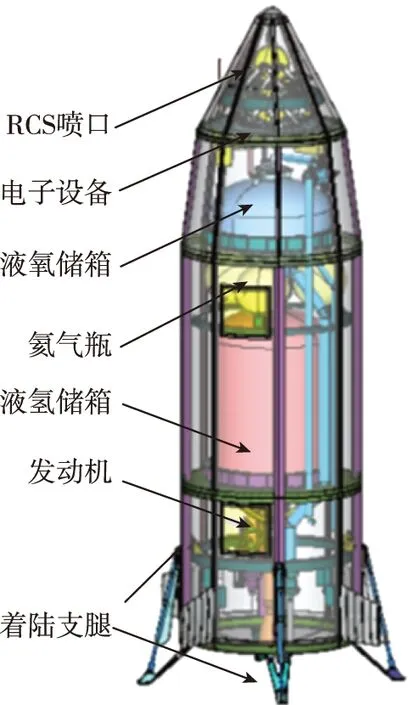
(c)RV-X

3.3 CALLISTO

CNES和DLR联合开发了验证飞行器CALLISTO(Cooperative Action Leading to Launcher Innovation in Stage Toss-back Operation)[62]，并且日本国家航天局JAXA在2017年也加入到了CALLISTO的研发中，该飞行器计划2022年具备验证条件，并开展10次左右的飞行试验，验证包括制导控制技术在内的垂直起降关键技术，降低未来发射风险。从图9看，3国航天机构各有侧重，但GNC技术由原本法国航天局开发变成法、德、日3国共同研发。

日本在参与CALLISTO 之前，JAXA也独立研发了RV-X飞行器(见图8(c))[63-64]，用于验证着陆段的制导控制技术，并计划开展百米高度的垂直起降飞行试验，这也为其后续开展国际合作积累了经验。

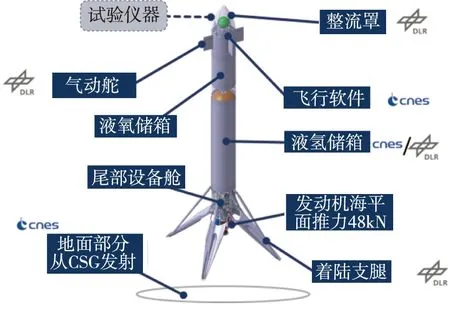
(a)CNES和DLR版本

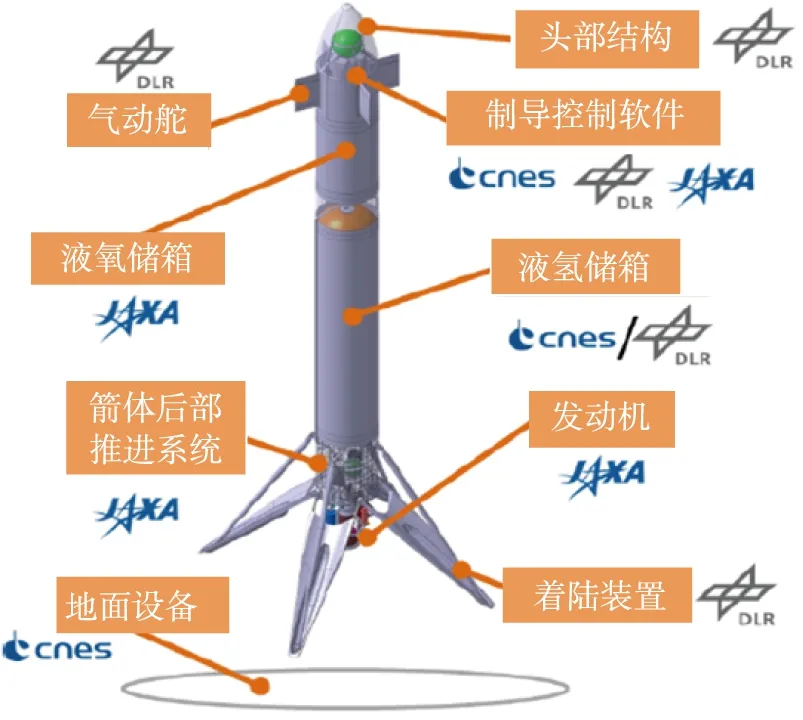
(b)法德日联合版本

3.4 THEMIS

法国航天局将未来可重复使用的芯一级火箭命名为THEMIS，采用7台可重复使用的液氧甲烷发动机Prometheus，计划于2023—2025年之间开展验证飞行，从而支撑新一代Ariane NEXT系列火箭的可重复使用。图10是其效果图，分别是火箭起飞和芯一级着陆[65]。

图10 CNES构想的重复使用一级飞行器THEMIS

总结各国垂直着陆技术的研发路线可以看出，各国科研机构均以验证制导控制技术为目的，专门研发了小型验证飞行器,并且在线轨迹规划技术作为着陆过程中的核心技术之一。美国和欧洲各国分别依托斯坦福大学和苏黎世理工大学实验室的力量，研发了基于嵌入式平台的在线轨迹规划求解器，提升着陆过程的精度和成功率。

4 结论

综合上述学术研究成果和各国开展的应用可以看出：基于数值优化的制导或在线轨迹规划方法已成为学术界主流研究方向，并逐渐得到了工程界的认可和应用。考虑凸优化算法能够保证收敛性的特点，垂直着陆问题的无损凸化方法研究和数值求解算法研究已成为工程领域和数值优化领域的重要方向，其中基于对偶内点法开发的凸优化求解器已成为在线轨迹规划算法的首选。结合我们自身开展的前期研究，得出如下结论：

1)基于模型的在线优化方法对模型的精度要求较高，预测模型的偏差将被引入到每个规划周期生成的最优控制指令中，从而不断累积至终端状态。此时，对于终端约束不严格、可行域较宽、控制能力有盈余的问题，通过在线滚动优化可以一定程度上消除预测模型偏差的影响。然而对于定点垂直着陆问题，终端约束条件的满足程度直接影响着陆过程的成功率，因此开展在线辨识算法的研究，实时修正预测模型十分必要。

2)为进一步提升凸优化计算效率，针对计算耗时最多的线性方程组求解问题，稀疏矩阵分解和迭代更新等算法的优化或者硬件化可能是有效手段；同时，适用于热启动(可以人为设定合理的初值)的交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)也是新的理论研究方向之一。

3)对于垂直着陆任务，推力可调是实现垂直着陆段的必要条件，其重要性要大于推力深度调节能力。调节深度的大小取决于算法的先进性。如果推力幅值固定，在偏差状态下仅能通过姿态调节来控制，但不能同时兼顾三通道控制要求，往往为克服纵向偏差将在水平方向引入更大的偏差。当推力幅值具备调节能力后，仅需较小的幅值调整范围就能够产生姿态大范围调节的控制效果，同时配合较小的姿态调整能够在偏差条件下满足各方向的控制要求。

4)推力调节的深度将主要影响从气动减速段至动力反推段的接入条件；调节范围越窄，对交接班条件的限制越严格。交班条件可看作是能够实现安全着陆的物理可行域，通常可表示为由速度和位置构成的多维空间；超出这个条件，不是优化算法找不到最优解，而是物理上不可行。此外，推力越大，动力反推的起点就越低，反推段的工作时间就越短。因此，可以根据控制算法的能力、发动机推力调节的难度以及气动减速段的控制精度选择一个最优的、可行的推力调节范围。对于当前我国发动机推力大、深度节流和调节性能较弱的情况，需要针对交接班条件开展研究。

5)不同的接入条件对偏差的适应能力差别较大，为保证着陆过程中对正、负向偏差均具有一定的适应能力，要求接入条件对应的标准推力尽可能处于调节范围的中值附近。

6)末段推重比越大，计算延时对精度的影响就越显著，因此需要研究计算延时的补偿算法。