考虑内压影响的加筋柱壳高效屈曲优化

2019-12-05杨木森

宇航总体技术 2019年6期

杨木森，张可，吴浩，郝鹏，王博，田阔

(1.大连理工大学工程力学系工业装备结构分析国家重点实验室，大连 116024;2.北京宇航系统工程研究所，北京 100076)

0 引言

网格加筋柱壳具有高比强度和刚度，被广泛应用于大直径运载火箭中，在大直径运载火箭中网格加筋壳的占重比也越来越高[1-2]。虽然网格加筋壳具有较好的承载性能，但结构的复杂也使网格加筋壳的失效模式变得复杂[2-3]。大直径运载火箭在飞行过程中，不断变化的轴内压耦合工况是火箭贮箱的典型服役工况[4]，整体失稳、蒙皮失稳、筋条失稳等均为其典型失效模式。随着箭体结构尺寸跨越式增大，采用有限元法进行精细模型屈曲分析的计算成本激增，不再适合大直径运载火箭的初始设计。因此，考虑内压影响的加筋柱壳高效屈曲优化对大直径运载火箭贮箱初始设计具有重要意义[3]。

运载火箭在发射、飞行过程中，其推进剂贮箱承受着发动机推进的轴压和箱内燃料液体的内压耦合作用，对这种轴内压耦合的工况，学者们研究了不同参数对柱壳结构失稳模式的影响，包括内压大小、材料强度及径厚比等。Abdi等[5]开展了3种不同加筋结构的失稳模式研究，认为加筋密度与结构的可靠性有直接关系。Rotter[6-7]研究了内压对柱壳贮箱底部的影响，认为内压会导致柱壳基部严重弯曲，发生前期弹塑性屈曲失效，从而形成“象脚型”屈曲。Khelil[8]研究了内压与非均匀轴压耦合工况下各向同性壳的临界应力。Franzoni等[9]提出了一种以振动相关技术为基础的非破坏性试验流程来评估含内压的正置正交加筋柱壳轴向屈曲载荷。因此，内压对贮箱加筋柱壳结构承载力的影响规律尚不明确，传统均匀加筋筒段难以适用于复杂的载荷工况，亟需发展适用内压工况的高承载效率的加筋策略。

针对加筋柱壳结构，等效刚度法(Smeared Stiffener Methond)是最常用的快速计算方法，该方法具有较高的分析效率[10]，其思路基于解析法对筋条进行刚度等效，再将筋条的等效刚度系数与蒙皮的刚度系数叠加，代入瑞利-里兹(Rayleigh-Ritz)公式计算得出整体屈曲载荷。传统的等效刚度法往往会导致预测屈曲结果普遍偏大，同时，对于不同的加筋构型，等效刚度法需要进行不同的解析推导，推导过程复杂，增加了选型与优化的难度，不适用于创新构型[11]。笔者先前工作基于渐近均匀化方法和瑞利-里兹法，建立了基于NIAH(Numerical Implementation Asymptotic Homogenization)的一种快速屈曲分析方法，该方法基于加筋单胞有限元模型进行等效，无须进行解析推导，相较于等效刚度法具有更高的等效精度[3,12]，但该方法仅适用于纯轴压下的加筋柱壳。目前,尚未有学者提出针对轴内压耦合工况的加筋柱壳承载力快速计算方法。

本文首先设计了非等厚筋条的加筋构型，并基于渐近均匀化法和瑞利-里兹法，建立了考虑内压影响的网格加筋柱壳整体失稳载荷快速计算方法，并与传统等效刚度法对比了计算效率和计算精度；然后，基于自适应加点的代理模型开展给定质量约束的大直径网格加筋柱壳极限承载力最大化设计；最后，分析了内压对同等网格参数(最优设计)的加筋柱壳整体失稳载荷的影响规律，并从失稳波形的角度解释了该规律的机理。

1 大直径加筋柱壳承载力快速计算方法

1.1 网格加筋柱壳整体失稳载荷的快速计算方法

针对轴内压下的网格加筋柱壳结构整体屈曲失稳载荷，求解流程如图1所示，具体过程如下[1]：

第一步，选择网格加筋柱壳的代表性单胞，并建立有限元模型；

第二步，基于渐近均匀化方法计算典型单胞的等效刚度系数；

第三步，将单胞等效刚度系数代入至Rayleigh-Ritz公式，计算得出整体屈曲载荷值和屈曲模态波数。

该方法不需要解析推导代表性单胞刚度阵，并适用于任意周期性的网格加筋类型，有限元分析仅计算单胞模型，较精细模型分析将大幅提高计算效率。

图1 基于NIAH的快速计算方法的流程图

针对圆筒壳在均匀轴压下的稳定性问题，学者们已做了大量的理论研究和试验研。针对正交各向异性筒壳结构，根据圆筒壳稳定性基本方程组[13]

(1)

K11=A11α2+A66β2

K22=A22β2+A66α2

K12=(A12+A66)αβ

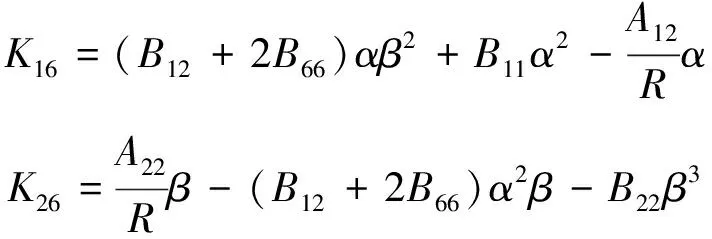
K66=D11α4+2(D12+2D66)α2β2+

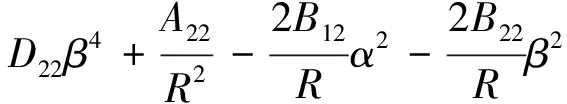
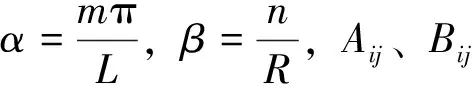
(2)

对于任意的正整数m和n，数值求解N的最小值Nmin，即为单位长度轴压临界轴力

Nij=Nmin

(3)

(4)

同理可求得初始内压工况下的单位长度轴压临界轴力

Nij=Nmin

(5)

1.2 网格加筋柱壳局部载荷的快速计算方法

在工程实际中，网格加筋柱壳失效模式多种多样，蒙皮局部失稳和筋条局部失稳是两种典型的局部失效模式。本节基于板壳屈曲理论，发展了非等厚筋条加筋柱壳的蒙皮局部稳定性和筋条局部稳定性的承载力理论计算公式。

1.2.1 蒙皮局部稳定性

当加筋类型为正置正交时，根据弹性力学四边简支板轴压屈曲理论[14]，蒙皮局部失稳时的单位长度轴力为

(6)

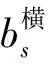
(7)

当加筋类型为等边三角形时，由文献[15]可知蒙皮单位长度临界轴力为

(8)

式中，C1=9.72。

考虑到竖筋和斜筋宽度不相同，如图2所示，由文献[15]可知斜筋的等效面积为B=Asin3θ，θ=30°，那么，加筋柱壳的单位长度轴力为蒙皮受力和筋条受力的总和

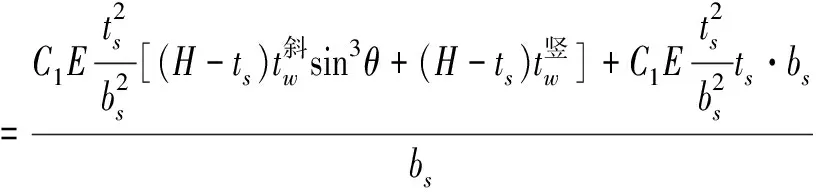
(9)

Tlj=2πRNlj

(10)

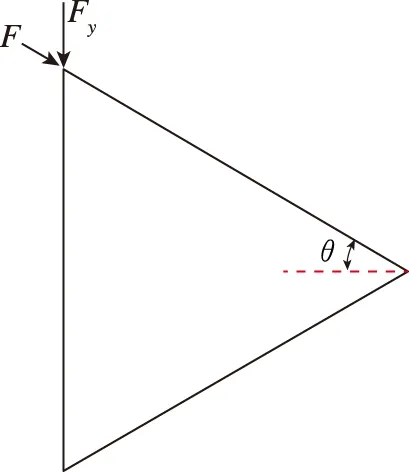
图2 等边三角单胞示意图

1.2.2 筋条局部稳定性

简化筋条轴压局部屈曲问题，将竖筋条局部失稳看作三边简支一边自由的矩形板轴压屈曲问题，其筋条局部失稳载荷为

(11)

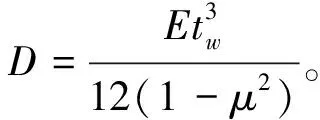
当加筋类型为正置正交时，竖筋屈曲失稳的单位长度轴力为

(12)

Tlj=2πRNlj

(13)

当加筋类型为等边三角形时，考虑到竖筋和斜筋宽度不相同，那么

(14)

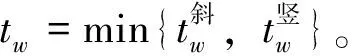
因此，加筋柱壳筋条局部失稳时的整体临界轴力为

Tlj=2πRNlj

(15)

1.3 快速计算方法精度验证

为了验证1.1节中提出的轴内压下的加筋柱壳快速计算方法预测精度，本节采用典型等边三角网格加筋壳模型，模型几何参数：直径D=4000mm，长度L=6000mm，蒙皮厚度ts=5.5mm，筋条高度H=44.5mm，筋条宽度tw=13mm，筋条间距bs=135mm。加筋柱壳的整体数值模型采用有限元仿真软件ABAQUS建立，蒙皮网格单元大小为50mm，筋条高度方向离散两个单元。设置底部简支、顶部简支且放松轴向位移的边界条件，计算线性屈曲载荷。

表1给出了轴内压下的加筋柱壳快速计算方法、线性有限元方法和等效刚度法的承载力计算结果的对比。图3为加筋柱壳整体失稳示意图。

图3 加筋柱壳整体失稳示意图

表1 失稳模式及计算时间对比

Tab.1 Comparison of buckling mode and calculation time

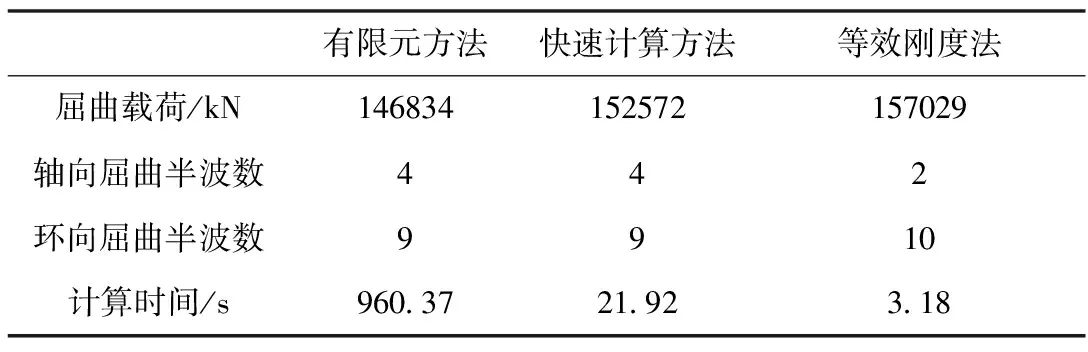
有限元方法快速计算方法等效刚度法屈曲载荷/kN146834152572157029轴向屈曲半波数442环向屈曲半波数 9910计算时间/s960.3721.923.18

从表1中可以看出，针对该模型，采用精细有限元模型计算方法耗时960.37s，所得屈曲载荷FFEM=146834kN。从图3加筋柱壳的失稳波形图中看出，环向半波数为9，纵向半波数为4。采用本文提出的快速计算方法耗时21.92s，所得屈曲载荷FRBAM=152572kN，相较于精细有限元模型所得承载力的误差为3.76%，环向半波数为9，纵向半波数为4；采用等效刚度分析方法耗时3.18s，所得屈曲载荷FSSM=157029kN，相较于精细有限元模型所得承载力的误差为6.94%，环向半波数为10，纵向半波数为2。对比这3种算法可以看出，快速计算方法相较于有限元方法，屈曲载荷计算结果仅差3.76%，计算效率提高了44倍，同时捕捉到轴向屈曲半波数与环向屈曲半波数与有限元结果相同；快速计算方法相较于等效刚度法，计算精度更高，同时捕捉到的轴向屈曲半波数与环向屈曲半波数更精准。

表2给出了快速计算方法与传统的等效刚度法的网格加筋筒等效刚度阵差异对比，发现两种方法计算的等效刚度阵中的A阵基本一样，传统的等效刚度法的B阵和D阵都比快速计算方法的大。由于传统的等效刚度法对筋条进行等效，难以准确描述筋条与蒙皮之间的耦合关系，且基于梁假设的解析方法对筋条的弯曲刚度估计过高，导致预测的屈曲载荷普遍偏大。

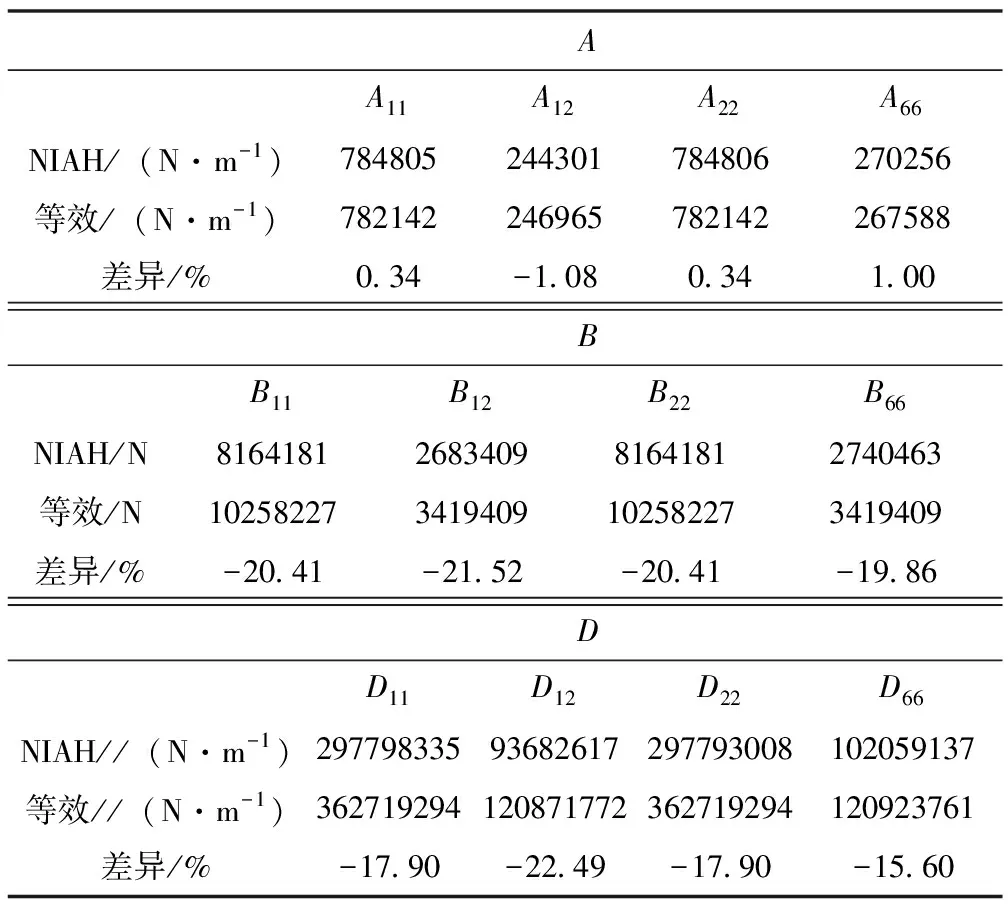
表2 快速计算方法与传统的等效刚度法的ABD阵差异分析

为验证本文提出的整体失稳载荷快速计算方法的适用性，针对加筋柱壳的筋条参数，基于最优拉丁超立方法抽取100个样本点进行误差分析。图4给出了本文提出的快速计算方法与有限元方法的相对误差，可以看出快速计算方法较有限元方法的相对误差均在10%以内，其中81个样本点的相对误差在5%以内。图5给出了等效刚度法与有限元方法的相对误差，可以看出等效刚度法较有限元方法有6个采样点的相对误差超过10%，最大误差可达40.23%，所有样本点相对误差均超过5%。上述误差分析说明，本文提出的快速计算方法预测误差鲁棒性更强，表明了本文提出的快速计算方法的可信性。

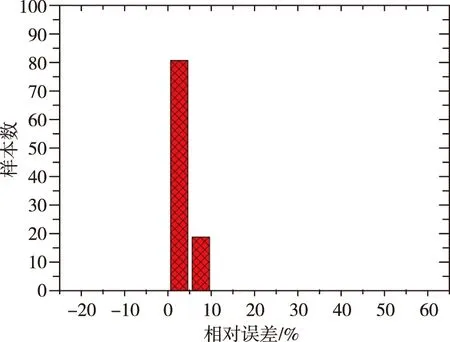
图4 快速计算方法与有限元方法的相对误差

图5 等效刚度法与有限元方法的相对误差

2 大直径网格加筋柱壳承载力快速优化设计

2.1 基于自适应代理模型的快速优化方法

动态代理模型以其高效的优化效率被广泛研究发展，其中应用最广泛的是Jones于1998年提出的高效全局优化方法[17-18](Efficient Global Optimization，EGO)，国内外许多学者发展并改进该算法应用于众多行业中[19-24]。该方法通过构造一种期望改进(Expected Improvement，EI)的加点准则，考虑了预测模型的均值和方差，寻找该准则的最大期望提高点作为新的样本点来更新预测模型，反复迭代直至结束。由于EI加点准则同时考虑了模型的预测最优值和误差性，该算法具有优异的全局和局部搜索能力。面向运载火箭贮箱的初步设计的高效率需求，本文基于加筋柱壳承载力快速计算方法，搭建了基于EGO代理模型的加筋柱壳高效优化设计框架，如图6所示。

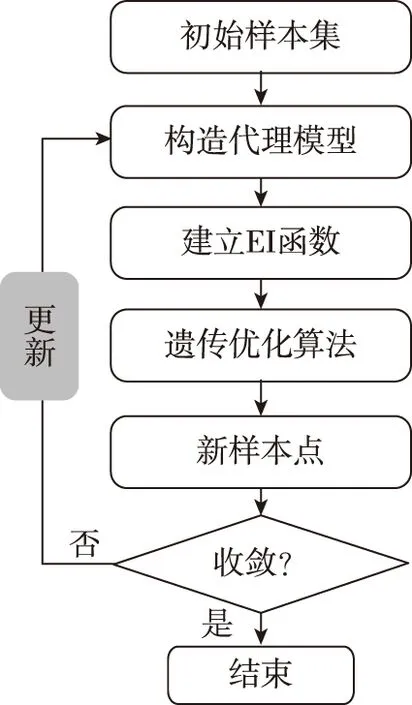
图6 基于EGO代理模型的快速优化流程

针对两种网格加筋类型，以筋条高度H、筋条宽度tw、筋条间距bs、蒙皮厚度ts为设计变量，以整体承载力和局部承载力都满足相应的设计要求为约束条件，开展内压为0.1MPa与轴压耦合工况下网格加筋结构轻量化设计，优化列式如下

(16)

式中，Tlj为整体和局部承载的临界轴力，Tsj为整体承载和局部承载的设计载荷。

2.2 加筋柱壳优化算例

本节采用直径D为9500mm，长度L为6000mm的两种加筋典型的柱壳算例，如图7所示。加筋柱壳承受0.1MPa内压和轴压耦合作用。材料选用铝合金，弹性模量E为68264MPa，泊松比μ为0.33。加筋柱壳可设计的变量分别为蒙皮厚度ts、筋条高度H、横筋宽度tw1、竖筋宽度tw2、筋条间距bs，优化质量约束为4299.00kg。加筋柱壳极限承载力采用1.1节中提出的快速计算方法，同时考虑局部失稳的情况。两种加筋类型的优化区间和最优设计参数如表3所示。

(a)正置正交

(b)等边三角

表3 两种加筋构型优化设计空间

由表3可知，最优解对应的结构均到达质量约束上限附近，材料得到充分利用。根据参数优化结果可以得出：对于本文的大直径筒壳模型，在0.1MPa内压与轴压耦合工况下，在相同的质量约束以及相同设计区间，等边三角形网格加筋轴压承载力优于正置正交网格加筋筒。

两种加筋类型的加筋柱壳迭代过程如图8所示，从图8中可以看出，随着样本点的不断加入，优化最终收敛。

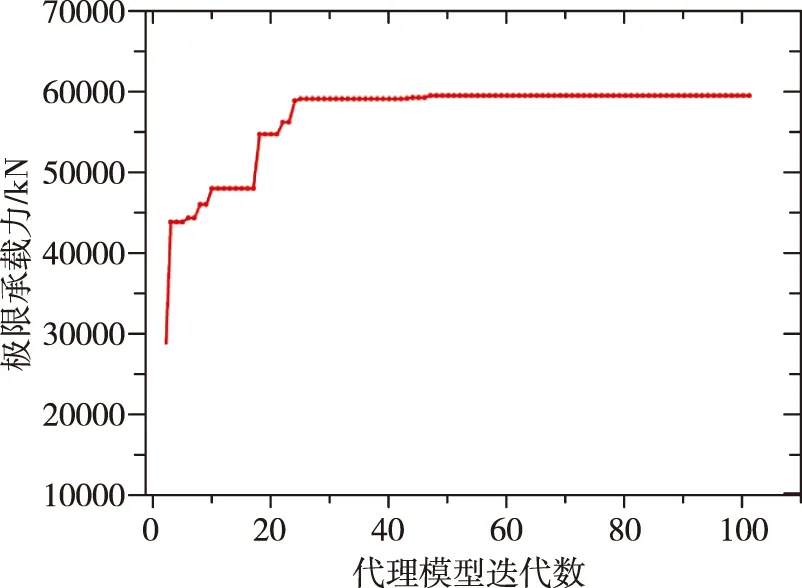
(a)正置正交

(b)等边三角

3 内压对大直径网格加筋柱壳承载力的影响规律

大直径运载火箭在飞行过程中，贮箱内燃料不断消耗随之内压逐渐降低，工况发生改变，因此需要探究内压对大直径网格加筋柱壳承载力的影响规律。由式(6)～式(15)可知，网格加筋柱壳的蒙皮局部失稳载荷和筋条局部失稳载荷与内压大小无关，因此，本节仅探究内压对网格加筋柱壳整体失稳载荷的影响规律。

本节以2.2节中的网格参数最优设计为例，采用了4种不同直径的加筋柱壳算例，直径D分别为4000mm、5000mm、7500mm和9500mm，长度L均为6000mm。基于快速计算方法获得的正置正交和等边三角形网格加筋柱壳结构整体失稳载荷随内压的变化规律如图9所示。

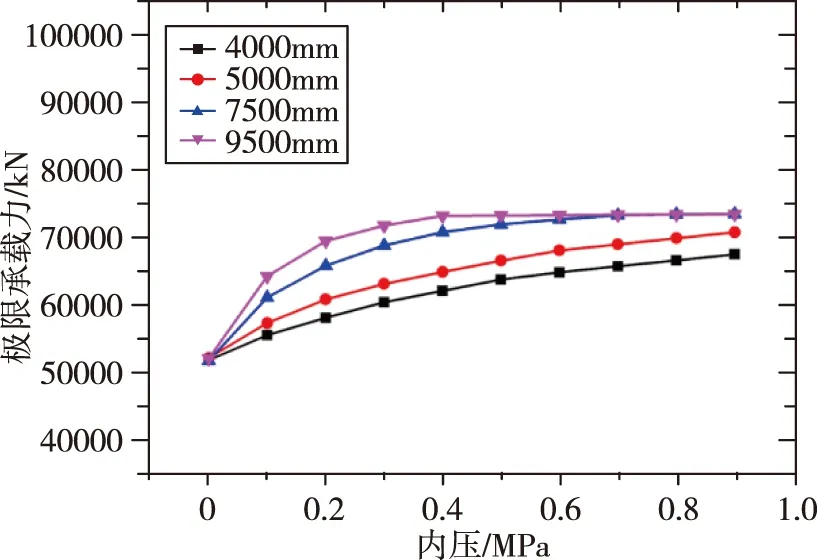
(b)等边三角

由图9可知，对于正置正交和等边三角两种加筋形式最优结构的加筋筒，内压为零时，随筒壳直径的增大整体失稳载荷基本不变；内压大于0.1MPa时，筒壳极限承载力随直径的增大，基本呈线性增长的趋势。对于正置正交最优结构的加筋筒壳，直径为9500mm时，加筋柱壳的整体失稳载荷随内压增大，增长的速度越来越慢。对于等边三角最优结构的加筋筒壳，直径为7500mm和9500mm时，内压大于0.7MPa后，随内压增大，筒壳整体失稳载荷基本不变。

由式(6)可知

(17)

Plj=2πR×Nlj=

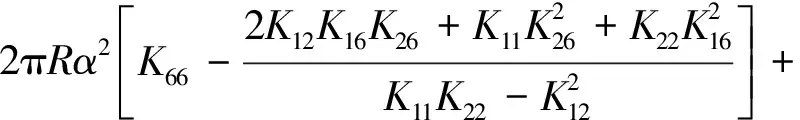
(18)

从式(17)和(18)中可以看出，纵横失稳波数比n2/m2是影响内压项的重要参数。本文从失稳模式出发，统计了每个直径和内压对应的失稳模式和失稳波数，失稳波形n2/m2变化规律如图10所示。从图10中可以看出，对于正置正交和等边三角加筋形式最优构型，内压越小，筒壳的n2/m2越大，表明随着内压的增加导致加筋柱壳的失稳波形发生转变，内压较小时内压随筒壳整体失稳载荷的贡献大，内压较大时整体失稳载荷的内压项大幅减小，最终呈现加筋柱壳整体失稳载荷先快速增加后基本不变。对于正置正交最优结构的加筋筒壳，n2/m2均大于1，因此极限承载力随内压增加一直增大。对于等边三角最优构型的加筋筒，当直径为7500mm和9500mm，内压大于0.7MPa时，n2/m2是一个小量，整体失稳载荷随内压的增加而基本保持不变。