巧用变式教学提高中考复习效率
2019-12-04朱明芬
摘 要:中考复习中,巧用变式教学,可以促进学生多角度地深化理解数学知识,建立相关知识之间的有机联系,构建解题的经验系统,使学生的思维向多层次、多方向发散。复习中教师应立足于教材,精选教材中的典型例题、习题,合理运用各种变式进行挖掘、延伸、改造,用问题编成变式题进行教学。充分调动学生的积极性,让学生主动参与教学的全过程,减轻学生负担,提高复习效率。
关键词:变式教学;中考复习;效率
一、 问题提出
中考复习对初中学生全面系统地整理数学知识、建立知识之间的联系、培养思维、提升能力有着积极的意义。然而,目前的中考数学复习中,一部分教师先是帮助学生罗列知识点,查漏补缺,然后就是做题,反复地做,达到熟能生巧。所以中考复习出现了这样的现象:课堂上老师不停地讲题,甚至把讲完了几套模拟仿真题作为完成教学任务的标准,课堂外,学生陷于题海中不能自拔,对解题产生了厌烦心理。这样复习,既没有帮助学生建立知识之间的有机联系,解决问题的能力也没有明显的提高,复习效率不高。
通过学习顾冷沅教授等有关变式教学的理论,结合自己的教学经验,我们采用变式教学进行中考复习,收到了良好的效果。
二、 变式教学
顾泠沅教授等对变式教学进行了系统而深入的实验研究与理论分析。他们系统地分析和综合了变式教学的概念,并确认和说明了两种变式:“概念性变式”和“过程性变式”。
(一) 概念性变式
对概念的多角度理解。概念性变式在教学中的主要作用是使学生获得对概念的多角度理解。
(二) 过程性变式
通过数学活动的有层次推进,深化相关数学知识、方法的理解。主要教学含义是在数学活动过程中,通过有层次的推进,使学生分步解决问题,积累多种活动经验。
过程性变式在教学中主要有以下三个方面的作用:
(1)用于概念的形成过程;
(2)用于问题解决的教学;
(3)用于构建特定的经验系统。用于构建特定经验系统的变式,既包括解题过程中的各种铺垫如引理、特殊化等,也包括对原问题的各种引申如改变条件、改变结论、一般化等。
三、 变式教学与中考复习
中考复习中,巧用变式教学,可以促进学生多角度地深化理解数学知识,建立相关知识之间的有机联系,构建解题的经验系统,使学生的思维向多层次、多方向发散。
从历年的中考试题来看,虽然出现了许多新题型,但绝大多数的题目取材于教材,试题的构成是在教科书中的例题、练习题、习题、读一读的基础上通过类比、加工改造、加强条件或减弱条件、延伸或扩展而成的。因此,复习中教师应立足于教材,精选教材中的典型例题、习题,充分调动学生的积极性,从而提高复习效率。
(一) 立足教材基本知识点,通过变式深化知识理解
数学基本知识点的掌握,关键在于明确理解其实质,如果仅靠学生的机械记忆,是不能熟练、灵活应用的,因此在复习基本知识点时,可利用变式,展示相关知识的联系以及结论成立依附的条件,培养学生辨析、判断、应用的能力。
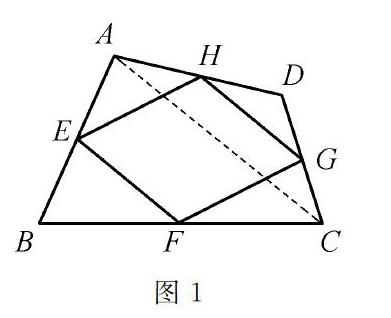
【例1】 如图1所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA边上的中点,求证:四边形EFGH是平行四边形。
本例题来自苏科版八年级(下),是简单的三角形中位线定理的应用,但同时又是研究中点四边形的基础,复习阶段学生很容易添辅助线AC,运用三角形中位线定理得到 EF∥GH 且EF=GH,从而证明四边形EFGH是平行四边形,但对中点四边形的理解与应用还远远不够,在此基础上,本题可以变式如下命题,请学生填写结论并想想如何证明。
(1)順次连接矩形四边中点所得的四边形是(菱形);
(2)顺次连接菱形四边中点所得的四边形是(矩形);
(3)顺次连接正方形四边中点所得的四边形是(正方形);
(4)顺次连接等腰梯形四边中点所得的四边形是(菱形);
通过变换四边形ABCD的形状,学生会发现四边形EFGH始终可用三角形中位线定理证得一组对边平行且相等从而证明是平行四边形,但却成为特殊的平行四边形,原因在于四边形ABCD的对角线的特殊性,学生慢慢感悟到EFGH的形状取决于四边形ABCD的对角线的特征而非四边形ABCD的形状,此时再变式如下:
(5)若AC=BD,AC⊥BD,则四边形EFGH是(正方形);
(6)若四边形EFGH为矩形,则(AC⊥BD);
(7)若四边形EFGH为菱形,则(AC=BD);
由于学生已抓住中点四边形的实质,很快地通过寻找四边形ABCD的对角线特征确定四边形EFGH的形状,反之由四边形EFGH的形状可以确定出四边形ABCD的对角线特征。此时学生探索中点四边形的热情高涨,较好地掌握了中点四边形的判断方法,同时也加深了特殊四边形的性质与判定的应用,还逐渐体会到构造三角形中位线在几何证明题中有着广泛的应用,故又作如下的变式:
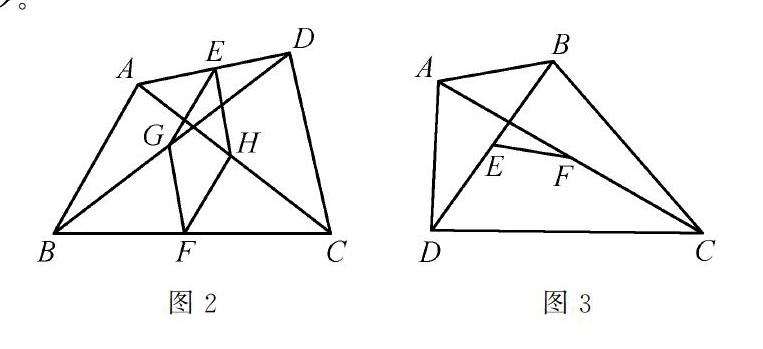
(8)如图2所示,在四边形ABCD中,若AB=CD,E,F,G,H分别为AD,BC,BD,AC的中点,求证:EFGH是菱形。
(9)如图3所示,在四边形ABCD中,CD>AB,E,F分别是BD,AC的中点,求证:EF>12(CD-AB)。
通过这组变式题的学习,一方面学生复习、巩固了三角形中位线和四边形知识,系统地整理四边形、平行四边形、矩形、菱形、正方形的概念及它们之间的联系;使学生充分掌握了四边形这一章节所有基础知识与基本概念、基本方法,沟通了不同知识点之间的内在联系,为进行数学问题演变奠定了坚实的知识基础。另一方面通过不断变换命题的条件,引申拓广,产生一个个既类似又有区别的问题,使学生产生浓厚的兴趣,在挑战中寻找乐趣,培养了思维的深刻性,充分发挥学生的积极性、主动性和创造性,使不同层次的学生都有收获,同时也进一步巩固了中点四边形的知识。
(二) 结合典型例题,着意设计阶梯式的变式问题,拓展学生的思维广度和深度
数学教学的重要任务之一就是培养学生的思维能力。事实上,一个好的例题教学可以起到牵一发而动全身的作用。在教学例题时,可以从一个简单的问题开始慢慢演变,通过“移步换景”,设置变式问题,激起学生强烈的探求欲望,让学生思维得以产生、维持,引向纵深,让学生在解决问题、获得方法的同时,提高思考问题的能力。
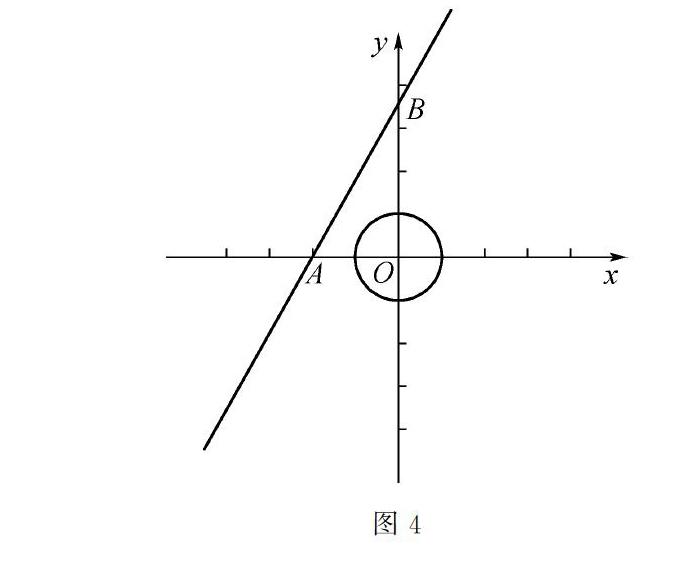
【例2】 如图4,在平面直角坐标系中,⊙O的半径为1,直线l:y=kx+b经过点A(-2,0)交y轴于B,将直线l绕点A按顺时针方向旋转的过程中,当b满足什么条件时,直线l与⊙O相离?相切?相交?
直线与圆的位置关系是中考的重要内容,在旋转的背景下,可引导学生先找到直线l与⊙O相切时的特殊情形,很容易得出直线l与⊙O相离、相切、相交时的b的条件,这样动中取静,把动态问题定格到特殊情况,学生容易掌握。在学生品尝到成功的喜悦时,我又设计如下变式:
变式一:平面直角坐标系中,⊙O的半径为1,直线l:y=3x+23与x轴、y轴交于A,B两点,将直线l沿x轴方向向右平移几个单位时,直线l与⊙O相交?
变式二:平面直角坐标系中,直线l:y=3x+23与x轴、y轴交于A,B两点,点P在直线l上,以点P(-1,3)为圆心,半径为R作⊙P,当⊙P被一条坐标轴截得的弦长等于2时,求R的值?
提高:平面直角坐标系中,直线l:y=3x+6与x轴、y轴交于A,B两点,以点P(5,1)为圆心,半径为1作⊙P,若⊙P以每秒2个单位的速度沿x轴负方向向左平移,同时直线l绕点A作顺时针方向旋转,当⊙P第一次与y轴相切时,直线l恰好也同时与⊙P相切,求直线l每秒旋转多少度?
变式:若⊙P以每秒2个单位速度沿x轴负方向向左平移,同时直线l沿x轴正方向向右平移,当⊙P第一次与y轴相切时,直线l恰好也同时与⊙P第一次相切,求直线l每秒平移几个单位长度?
由于采用了变式题的设计,学生在课堂教学中的参与意识得到有效加强,学生的求知欲望强烈,使他们的应变能力得以提高,进而提高复习效率。
(三) 立足基本解题方法,运用变式教学,提升学生解题能力
在大量的习题中,有不少题目存在着共同的解题规律,不妨称这种题目为同类题。在复习中,教师要善于将习题分类归档,并集中精力解决同类题中的本质问题,或通过解其中一道题,总结出解这一类问题的方法和规律,使学生牢固掌握了基本题型及基本解题规律,揭示了知识之间的内在联系,前后贯通、引申拓展,形成较为完整的知识链,达到了举一反三、触类旁通、复习一例、解决一类的目的。
四、 几点思考
1. 设计变式题时最好以教材为源,要深入挖掘教材中的典型的例题、习题,体现“源于课本,高于课本”的原则,重视通性、通法。
2. 对例题、习题进行变式时,可以采用变条件、变结论、变图形、变式子、变表达方式等多种形式,最好在一堂课中从简单到综合进行变式教学,给课堂注入新意,让学生感到数学复习内容“旧貌变新颜”。
3. 设计变式题时要注意两个“度”,数量要适度,难度要恰当。变式过多过难,不但给学生造成过重的学习和心理负担,而且还会使学生产生逆反心理,对解题产生厌烦情绪,反而适得其反。
总之,根据教材的内容和学生的情况来安排因材施教是课堂上永远要坚持的原则。实践证明,在复习阶段恰当合理的问题变式可以一改学生复习课中被动接受的学习方式,有助于学生把知识学活,提高学生学好数学的信心和能力。
参考文献:
[1]顾泠沅,黄荣金,费兰伦斯·马顿.变式教学:促进有效的数学学习的中国方式[J].云南教育(中学教师),2007(3).
[2]鲍建生,黄荣金,易凌峰,等.变式教学研究[J].数学教学,2003(1).
[3]汤炳兴.“中学数学复习”访谈与建议[J].中学数学教学参考,2002(09).
作者簡介:
朱明芬,江苏省常熟市,江苏省常熟市孝友中学。
