幂函数递减模型的建立、对比与应用

2019-12-04陈元千傅礼兵

油气地质与采收率 2019年6期

陈元千，傅礼兵

（中国石油勘探开发研究院，北京 100083）

产量递减法是预测油气井、油气藏和油气田产量和可采储量的重要方法。它的应用不受油气藏的储集类型、驱动类型、流体类型和开采方式的限制，只要进入了产量递减阶段，即可进行方法的选择和有效的应用。Arps［1-2］于1945 年和1956 年提出了指数、双曲线和调和三种经典递减模型。其中指数递减模型应用最为广泛，而双曲线递减模型应用较少，调和递减模型出现的概率很低。这主要与三种递减模型的适用性和预测结果的可靠性有关。陈元千等于2015 年提出的线性递减模型［3］，仅适用于压裂后投产而产量递减较快的致密性砂岩和页岩的油气井和油气藏。陈元千等于2016 年建立的广义递减模型［4-5］，对注水开发油田的加密调整效果［6］、注聚合物溶液的三次采油效果［7］和重质原油热力开采的效果［8-9］可以作出有效评价。对于致密、超致密的砂岩油气藏和页岩油气井，若在经水力压裂投产后，产量较低，递减较快，可采用线性或指数递减模型进行评价［10］。而对于投产后产量递减较慢的页岩水平气井，可利用笔者建立的幂函数递减模型，进行产气量、累积产气量和经济可采储量、采出程度和递减率的预测。

1 幂函数递减模型的建立

Pareto于1897年提出的负指数幂函数表达式［11］为:

由（1）式可以看出，当x=0 时，y趋于无穷大，这是该函数的一个特点，也是它的一个缺陷。为了将（1）式用于产量递减，对（1）式作如下修正:

这样，由（2）式可以看出，当x=0时，y=a，而不是无穷大。若将y改为产量q，x改为时间t，由（2）式得幂函数递减的产量为:

由（3）式可以看出，当t=0 时，q=a，而a就是t=0时的初始理论产量qi。为了确定（3）式中常数a和b值，将该式取自然对数得:

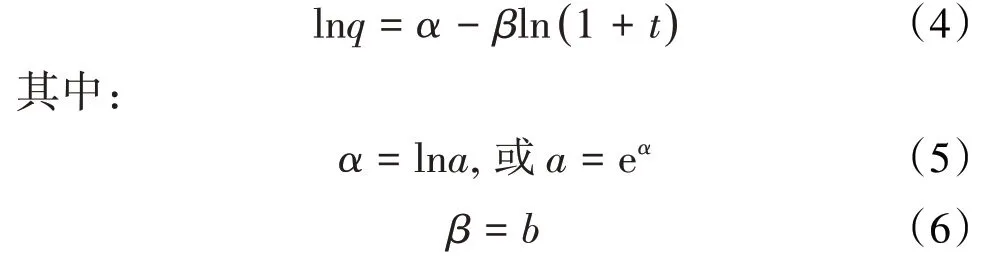
由（4）式可以看出，q与（1+t）之间呈双对数直线关系，故幂函数递减又可称为双对数递减。

已知累积产量与产量的关系为:

将（3）式代入（7）式，经积分后得幂函数递减的累积产量为:

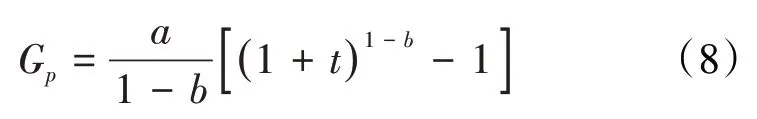
若经过经济评价确定了经济极限产量qEL后，那么，由（3）式可得与其相对应的经济极限生产时间为:

将（9）式代入（8）式，得幂函数递减的经济可采储量为:

由（8）式除以（10）式，得可采储量的采出程度为:

由（3）式对时间求导得:

已知Arps定义的递减率［1］为:

将（3）式和（13）式代入（12）式，得幂函数的递减率与时间的关系式为:

由（14）式可以看出，幂函数递减的递减率随时间的增加呈双曲线降低，当t=0 时，D=Di=b，故由（14）式得:

2 不同递减模型的对比

表1列出了按Arps递减指数划分的不同递减模型:n=-1 时为线性递减；n=0 时为指数递减；0＜n＜1时为双曲线递减；n=1 时为调和递减；1＜n≤2 而n=1/Di时为幂函数递减。表1 中的无因次产量qD=q/qi，无因次递减率DD=D/Di，无因次时间tD=Dit。

表1 不同递减模型的n，D，DD，q和qD的对比Table1 Comparisons of n，D，DD，q and qD for different decline models

绘制不同递减模型的无因次产量与无因次时间的典型曲线。由图1 可看出，线性递减（n=-1）的典型曲线处在最左边，其次是指数递减（n=0）的典型曲线，接着是双曲线递减（n=0.5）和调和递减（n=1）的典型曲线，最右边的是幂函数递减（n=2）的典型曲线。利用实际生产的产量递减数据与典型曲线拟合［12］，可以判断递减模型，确定递减常数和评价可采储量。

图1 不同递减模型无因次产量qD与无因次时间tD的关系Fig.1 Plot of qD and tD of different decline models

绘制不同递减模型的无因次递减率DD与无因次时间tD的关系曲线。由图2 可以看出，不同递减模型的递减率随时间变化的理论关系，幂函数递减是递减最慢的一种递减模型。

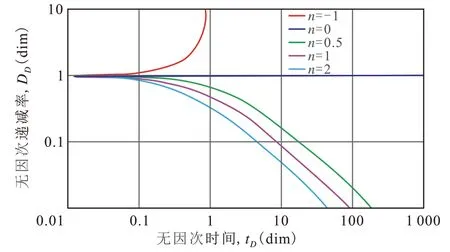
图2 不同递减模型的无因次递减率DD与无因次时间tD的关系Fig.2 Plot of DD and tD of different decline model

3 应用实例

美国宾夕法尼亚州阿巴拉琴盆地的Marcellus页岩气藏［13］，A 井和B 井两口页岩水平气井投产后的生产数据绘于图3。按照（4）式的关系，将两口井的生产数据绘于双对数坐标系统中，由图4看出，在双对数坐标系统中，两口井的q与1+t具有很好的直线关系，经（4）式的线性回归求得A 井的α=6.760 8，β=0.522 6，相关系数r=0.983 3；B 井的α=6.138 1，β=0.526 6，相关系数r=0.985 7。由（5）式和（6）式分别求得:A 井的a=863.33 和b=0.526 6；B 井的a=462.88和b=0.522 6。

图3 A井和B井产量曲线Fig.3 Production curves of Well A and Well B

图4 A井和B井的lnq与ln（1+t）的关系Fig.4 Plot of lnq vs.ln（1+t）of Well A and Well B

将两口井的a和b值分别代入（3）式，得预测A井和B井的产量关系式分别为:

再将A 井和B 井的a和b值分别代入（6）式，得预测两口井的累积产量关系式分别为:

最后，将两口井的a，b和qEL值分别代入（11）式，得预测A井和B井的采出程度关系式分别为:

将两口井的b值分别代入（11）式，得预测A 井和B井的递减率的关系式分别为:

将（16）式和（17）式预测两口井的产量数据绘于图3。由图3看出，预测结果与实际生产数据符合得较好。由（18）式和（19）式预测两口井的累积产气量绘于图5。由图5可以看出，预测结果与实际生产数据也符合得很好。由（20）式和（21）式预测两口井的采出程度绘于图6。由（22）式和（23）式预测两口井的递减率绘于图7。由图7看出，尽管两口井的产气量与可采储量相差明显，但递减率曲线几乎重合。

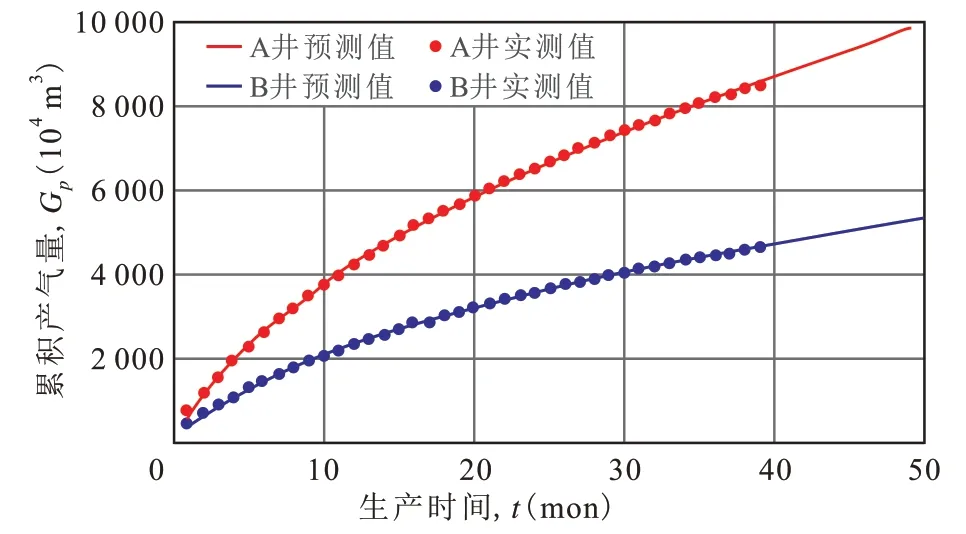
图5 A井和B井的Gp与t的关系图Fig.5 Plot of Gp vs.t of Well A and Well B

图6 A井和B井的R与t的关系图Fig.6 Plot of R vs.t of Well A and Well B

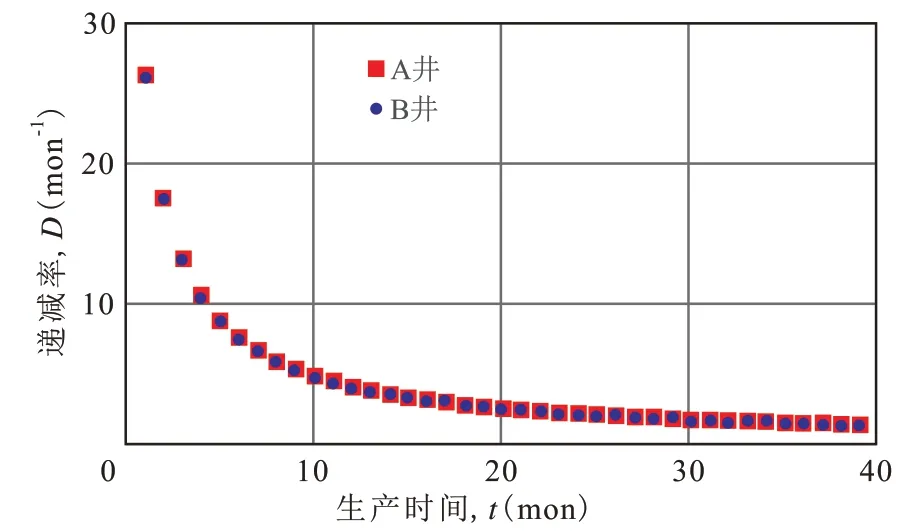
图7 A井和B井的D与t的关系图Fig.7 Plot of D vs.t of Well A and Well B

若设页岩水平气井生产的月经济极限产量qEL=30×104m3/mon，将该值与两口井的a和b值分别代入（10）式，可得A井和B井的经济可采储量分别为:

4 结论

通过对Pareto 于1897 年提出的负指数幂函数的修正和推导，建立了幂函数递减模型。该递减模型是对由Arps 提出的指数递减、双曲线递减、调和递减模型以及由陈元千提出的线性递减模型所构成的递减模型序列的重要补充和完善。Arps 提出的递减指数n是判断和划分递减模型的重要参数。递减指数愈大，产量的递减愈慢。线性递减的n=-1，双曲线递减的0＜n＜1，调和递减的n=1，幂函数递减的1＜n≤2。因此，幂函数递减是最慢的一种递减模型，而且产量开始递减得快，而后逐渐变慢。

实际工作经验表明，利用Arps 的指数递减和双曲线递减模型，以及陈元千的线性递减模型，对于页岩水平气井的产量和可采储量的预测，有时达不到比较可靠的结果。然而，利用笔者建立的幂函数递减模型，对两口页岩水平气井的产量、累积产量、经济可采储量和递减率的预测，取得了比较满意的结果。两口井的递减指数几乎相同，接近于2，属于递减最慢的类型。预测两口井的经济可采储量并不高，分别为3.554 3×108m3和1.083 7×108m3，这可能与两口水平井的水平段较短有关。

符号解释

y—幂函数的因变量；

x—幂函数的自变量；

q—气井的产量，104m3/d或104m3/mon；

qi—气井的初始理论产量（qi=a），104m3/d或104m3/mon；

qD—气井的无因次产量，dim；

qEL—气井的经济极限产量，104m3/d或104m3/mon；

Gp—气井的累积产量，104m3；

GR—气井的经济可采储量，104m3；

t—生产时间，d或mon；

tD—无因次生产时间，dim；

tEL—经济极限的生产时间，d或mon；