精细语言中智数及其多属性决策方法
2019-12-04樊长兴
樊长兴
(绍兴文理学院 计算机科学与技术系,浙江 绍兴 312000)
0 引言
由于客观事物的复杂性和人类思维的模糊性,很难用准确的数字来评价客观事物.于是,Zadhe教授创造性地提出了模糊集(FS)理论来处理模糊信息[1].此后不久,Atanassov教授进一步提出了包含隶属度和非隶属度的直觉模糊集(IFS),但直觉模糊集没有考虑信息的不确定性[2].为了找到一种更精确的表示方法,Smarandache教授采用标准或非标准的实数子集提出了中智集(NS)概念[3].与IFS相比,NS增加了一个不确定度来表示不确定的信息.近几年,关于中智集的研究涌现出很多[4-12〗.然而,当处理多属性决策问题时,有些属性可能包含一些子属性.例如,当考虑某一技术属性时,可能要从两个方面去考虑,即技术属性要细分成技术知识和技术能力这两方面.为了使决策结果更精确,当某一属性含有子属性时,需要同时考虑子属性所带来的影响,于是叶军教授和Smarandache教授提出了精细单值中智集(R-SVNS),其中隶属度L(t)被细化为L1(t),L2(t),...Lk(t),不确定性M(t)被细化为M1(t),M2(t),...Mk(t)和非隶属度(t)被细化为1(t),2(t),...k(t)[13].接着,樊和叶定义了精细区间中智集(R-INS)[14].陈、叶和杜提出了精细精简中智集(RSNS),使用精细精简中智集,可以同时表达精细单值中智集和精细区间中智集[15].在处理多属性决策问题时,一些属性评估值不能完全用纯粹的数值来表示,只能使用模糊的语言信息去评估.针对此情况,Zadeh教授提出了语言集(LS)[16].此后,出现了许多将语言集与其他集合组合在一起应用在多属性决策中的研究[17-22].只是文献[17-22]都不能表达纯粹的语言评估值.于是,叶军教授提出了语言中智数(LNN)并将它应用于多属性决策中[23].随后,很多基于语言中智数的集成算子被学者提出[24-25].但是,现有的基于语言中智数的决策方法都不能解决存在子属性的多属性决策问题.当决策属性具有子属性时,应该同时要考虑子属性对多属性决策问题的影响.为了解决这个问题,本文第一次提出了精细语言中智数以及它的运算规则,然后提出了两种基于精细语言中智数集成算子并研究了它们的性质.
1 基础知识
1.1 精细精简中智集和语言中智数
定义1[15]:设T为给定论域,t是T中的任一基本元素,精细精简中智集可以表示为:
其中t∈T,tk∈t={t1,t2,…,tp}(k=1,2,…,p),p是一个自然数.隶属度LR(t1),LR(t2),…,LR(tp):T→[0,1],不确定性MR(t1),MR(t2),…,MR(tp):T→[0,1],非隶属度R(t1),R(t2),…,R(tp):T→[0,1].
(1)当LR(t1),LR(t2),…,LR(tp)∈[0,1],MR(t1),MR(t2),…,MR(tp)∈[0,1],R(t1),R(t2),…,R(tp)∈[0,1],R表示精细单值中智集[13].
(2)当LR(t1),LR(t2),…,LR(tp)⊆[0,1],MR(t1),MR(t2),…,MR(tp)⊆[0,1],R(t1),R(t2),…,R(tp)⊆[0,1],R表示精细区间中智集[14].
定义2[15]:设
为两个精细精简中智数,它们具有如下关系:

定义3[23]:设语言集S={sj|j∈[0,f]},其中f是一个偶数.则m=sL,sM,s表示语言中智数,令sL,sM,s∈S,L,M,∈[0,f],其中sL,s,sM分别表示隶属度,非隶属度和不确定性.
定义4[23]:设m=sL,sM,s,m1=sL1,sM1,s,m2=sL2,sM2,s为三个语言中智数,φ≥0,则语言中智数的运算规则定于如下:
m1⊕m2=sL1,sM1,s⊕sL2,sM2,s
(1)
m1⊗m2=sL1,sM1,s⊗sL2,sM2,s
(2)
(3)
(4)
定义5[23]:设m=sL,sM,s,则语言中智数的得分函数和精确函数定义如下:
Q(m)=(2×f+L-M-)/(3×f),Q(m)∈[0,1],
(5)
Y(m)=(L-M)/f,Y(m)∈[-1,1].
(6)
定义6[23]:设m1=sL1,sM1,s,m2=sL2,sM2,s为两个语言中智数,
当Q(m1)>Q(m2),则m1≻m2;
当Q(m1)=Q(m2),Y(m1)>Y(m2),则m1≻m2;
当Q(m1)=Q(m2),Y(m1)=Y(m2),则m1~m2;
1.2 精细语言中智数及其运算规则
作为语言中智数的拓展,本文提出了精细语言中智数.
定义7:设T为给定论域,语言集S={sj|j∈[0,f]},其中f是一个偶数,则精细语言中智集定义如下:
其中SLR(t1),SLR(t2),…,SLR(tp),SMR(t1),SMR(t2),…,SMR(tp),S,S,…,S∈S,LR(t1),LR(t2),…,LR(tp),MR(t1),MR(t2),…,MR(tp),R(t1),R(t2),…,R(tp)∈[0,f],t∈T,tk∈t={t1,t2,…,tp}(k=1,2,…,p),p是自然数,SLR(t1),SLR(t2),…,SLR(tp)表示隶属度,S,S,…,S表示非隶属度,SMR(t1),SMR(t2),…,SMR(tp)表示不确定性.
作为R中的一个基本元素,并称之为精细语言中智数(RLNN).

(7)
(8)
(9)
(10)
2 精细语言中智数加权算术平均(RLNNWAA)算子和精细语言中智数加权几何平均(RLNNWGA)算子

(11)

根据定义8和9,可以得到如下相关定理.

(12)
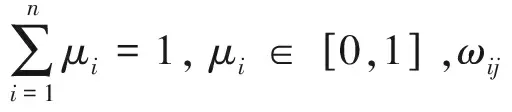
证明:
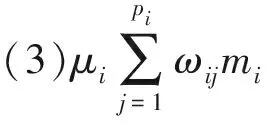

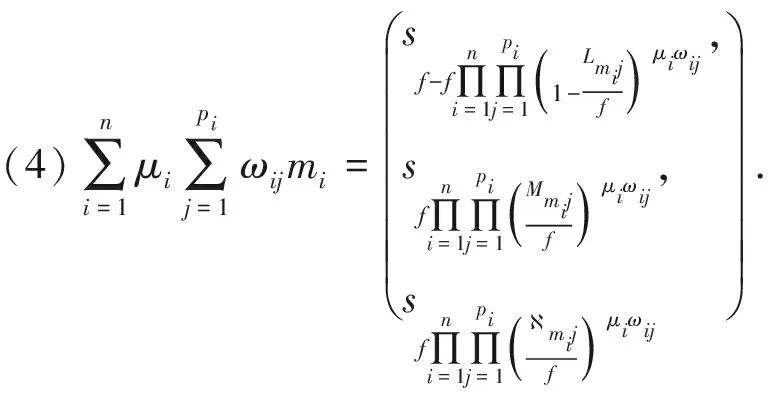
定理1证明结束.

证明:
因为对于任意的i,存在mi=m,所以能得到:
定理2证明结束.
定理3:存在两个精细语言中智数集合(m1,m2,…mn)和(k1,k2,…kn),如果miki(i=1,2,…,n),则RLNNWAA(m1,m2,…mn)RLNNWAA(k1,k2,…kn).
证明:
因为miki(i=1,2,…,n),能很容易得到:
ωijmi
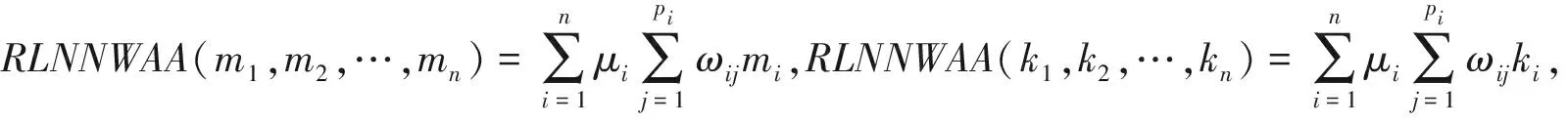
定理3证明结束.

证明:
设mmin=min(m1,m2,…mn),mmax=max(m1,m2,…mn)
根据定理2,能得到:
mmin=RLNNWAA(mmin,mmin,…,mmin),mmax=RLNNWAA(mmax,mmax,…,mmax)
根据定理3,能得到:
RLNNWAA(mmax,mmax,…,mmax)≥RLNNWAA(m1,m2,…mn)≥RLNNWAA(mmin,mmin,…,mmin).
所以max(m1,m2,…mn)≥RLNNWAA(m1,m2,…mn)≥min(m1,m2,…mn).
定理4证明结束.
(13)

根据定义8和10,可以得到下面的相关定理:

(14)

因为定理5的证明方法跟定理1类似,所以这里就不再重复证明.

RLNNWGA(m1,m2,…mn)=RLNNWGA(m,m…m)=m.
定理7:存在两个精细语言中智数集合(m1,m2,…mn)和(k1,k2,…kn),如果miki(i=1,2,…,n),则RLNNWGA(m1,m2,…mn)RLNNWGA(k1,k2,…kn).

RLNNWGA算子的相关特性证明与RLNNWAA算子类似,这里就不重复证明.
3 基于RLNNWAA算子和RLNNWGA算子的多属性决策方法
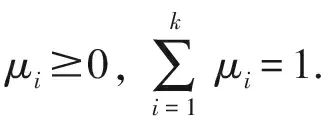
然后,应用精细语言中智数加权算术平均算子和精细语言中智数加权几何平均算子来解决多属性决策问题.根据这两个算子的集成结果,使用公式5或公式6来计算得分函数或精确函数的值,然后根据计算值,对备选方案进行排序,
表1 决策评估矩阵R

e1(e11,e12,…,e1p1)…ek(ek1,ek2,…,ekpk)M1(sTm111,sTm112,…,sTm11p1),(sIm111,sIm112,…,sIm11p1),(sFm111,sFm112,…,sFm11p1)…(sTm1k1,sTm1k2,…,sTm1kpk),(sIm1k1,sIm1k2,…,sIm1kpk),(sFm1k1,sFm1k2,…,sFm1kpk)M2(sTm211,sTm212,…,sTm21p1),(sIm211,sIm212,…,sIm21p1),(sFm211,sFm212,…,sFm21p1)…(sTm2k1,sTm2k2,…,sTm2kpk),(sIm2k1,sIm2k2,…,sIm2kpk),(sFm2k1,sFm2k2,…,sFm2kpk)…………Mn(sTmn11,sTmn12,…,sTmn1p1),(sImn11,sImn12,…,sImn1p1),(sFmn11,sFmn12,…,sFmn1p1)…(sTmnk1,sTmnk2,…,sTmnkpk),(sImnk1,sImnk2,…,sImnkpk),(sFmnk1,sFmnk2,…,sFmnkpk)
最终得出最好的选择.决策步骤如下:
步骤1:根据子属性的权向量ωi=(ωi1,ωi2,…,ωij)T(i=1,2,…,k; j=1,2,…,pi)和属性的权向量μ=(μ1, μ2,…, μi)T(i=1,2,…,k),结合精细语言中智数加权算术平均算子或者精细语言中智数加权几何平均算子,得到语言中智数mb:
步骤2:根据公式5,计算出mb的Q(mb)值.mb=RLNNWAA(mb1,mb2,…,mbk)
(15)
或者
mb=RLNNWGA(mb1,mb2,…,mbk)
(16)
步骤3:根据Q(mb)值对备选方案进行排序,选出最好的选项.
4 实例
本节采用的例子改编于文献[15],通过这个例子来验证本文所提出方法的可行性.现在,一所高校图书馆需要从4个候选图书供应商{M1,M2,M3,M4}中选择一个最优的图书供应商来进行图书采购.然后,他们邀请一些专家来对这些书商进行评估,这些专家需要分别给出图书供应商在综合实力、服务水平、价格这3个属性的评估值,这3个属性构成属性集{e1,e2,e3},而这3个属性都包含子属性综合实力包含两个子属性:企业规模(e11)和图书品种(e12);服务水平包含三个子属性:到货率(e21),编目数据规范(e22)和文献加工服务水平(e23);价格包含两个子属性:书籍折扣率(e31)和书籍加工费(e32).首先,这些专家通过基于语言集(LS)的精细语言中智数来评估这些子属性,其中LS={ε0=相当差,ε1=非常差,ε2=差,ε3=比较差,ε4=中等,ε5=比较好,ε6=好,ε7=非常好,ε8=相当好}.表2表示精细语言中智决策评估矩阵R.
属性的相对权值为μ=(0.4,0.3,0.3),子属权值分别为ω1=(0.6,0.4),ω2=(0.25,0.4,0.35)和ω3=(0.45,0.55).
根据上述条件和本文所提出的方法,做出以下决策.
步骤1:使用精细语言中智数加权算术平均算子,得到一组语言中智数mb:
m1=(ε8.0000,ε1.8845,ε2.3498),m2=(ε8.0000,ε1.7489,ε1.7720),
m3=(ε8.0000,ε1.8712,ε2.0215),m4=(ε8.0000,ε1.6836,ε2.1661).
步骤2:使用公式5,计算出得分函数Q(mb)(b=1,2,3,4)的值:
Q(m1)=0.8236,Q(m2)=0.8533,Q(m3)=0.8378,Q(m4)=0.8396;
表2 决策评估矩阵R

e1e2e3(e11,e12)(e21,e22,e23)(e31,e32)M1(ε6,ε7),(ε2,ε1),(ε2,ε3)(ε8,ε7,ε8),(ε1,ε3,ε2),(ε2,ε2,ε1)(ε6,ε8),(ε3,ε2),(ε3,ε4)M2(ε8,ε7),(ε1,ε2),(ε3,ε2)(ε7,ε8,ε7),(ε2,ε4,ε3),(ε1,ε2,ε1)(ε8,ε8),(ε1,ε2),(ε1,ε2)M3(ε,ε8),(ε1,ε3),(ε3,ε4)(ε8,ε6,ε7),(ε3,ε1,ε1),(ε2,ε1,ε2)(ε8,ε7),(ε4,ε3),(ε2,ε1)M4(ε7,ε6),(ε1,ε2),(ε2,ε3)(ε7,ε8,ε7),(ε2,ε2,ε1),(ε1,ε2,ε2)(ε7,ε7),(ε2,ε3),(ε2,ε3)
根据计算结果,得到排序顺序Q(m2)>Q(m4)>Q(m3)>Q(m1),可以看出M2即为最适合的图书供应商.
现在使用精细语言中智数加权几何平均算子.
步骤1’:使用精细语言中智数加权几何平均算子,得到一组语言中智数mb:
m1=ε6.9183,ε2.0613,ε2.5954,m2=ε7.6449,ε2.0597,ε1.9711,
m3=ε6.9575,ε2.3267,ε2.3759,m4=ε6.9398,ε1.8598,ε2.2794.
步骤2’:使用公式5,计算出得分函数Q(mb)(b=1,2,3,4)的值:
Q(m1)=0.7609,Q(m2)=0.8173,Q(m3)=0.7606,Q(m4)=0.7834.
根据计算结果,得到排序顺序Q(m2)>Q(m4)>Q(m1)>Q(m3),可以看出M2即为最适合的图书供应商.
与文献[13-15]相比,本文使用精细语言中智数对属性进行评估,并使用精细语言中智数加权算术平均算子和精细语言中智数加权几何平均算子来处理多属性决策问题,这种方法可以通过使用精细语言中智数来表达纯粹的语言信息.与文献[23-24]相比,在多属性决策中,当多属性包含子属性时,精细语言中智数加权算术平均算子和精细语言中智数加权几何平均算子可以处理这些问题,但是文献[23-24]确不能处理子属性相关问题.
5 结论
本文定义了精细语言中智数、精细语言中智数加权算术平均算子和精细语言中智数加权几何平均算子,然后研究了这些算子的相关属性.此外,还使用这两种算子来解决精细语言中智数环境下的多属性决策问题.最后,使用一个实例来验证所提出的方法的可行性.在处理多属性决策问题时,当属性包含子属性时,本文提出的方法可以通过精细语言中智数获得更精细的评估值,并使结果更加合理.
