审计师变更对异常审计收费的影响分析
2019-12-04张伟叶青
张 伟 叶 青
(1.绍兴文理学院 元培学院,浙江 绍兴 312000;2.中国农业银行绍兴市分行新昌县支行,浙江 绍兴 312500)
随着经济不断发展,审计结果的使用对象也慢慢从单一的被审计公司转变为社会公众、债权人、政府等各方,审计结果也作为成果呈现在公众面前.由于各种影响因素的存在,竞争性市场中呈现出低价揽客或高价收费的现象,从而导致异常审计收费的出现.研究异常审计收费的影响因素,有利于证券市场监管部门对审计师以及审计机构(如会计师事务所)的有效监督,也有助于我们了解审计市场审计收费的现状以及证券市场参与者参与审计服务的积极性.
1 文献回顾
在分析了审计费用有关的研究成果后发现,大部分研究成果侧重于研究影响审计收费的要素.Simunic[1]指出,审计收费与公司规模、盈利能力等要素有关.后来一些研究人员慢慢地将研究方向拓展至公司的内部控制、事务所合并等方面.
国内有关于审计收费的研究侧重于从公司层面和事务所层面来分析.在公司层面上,张爱华[2]认为公司的规模占主要因素,公司规模越大,业务量越大,审计师需要花更多的时间去进行审计测试,从而导致可能出现的误报和需要调整的事项会直接影响审计收费.也就是说审计风险会加大,同时审计费用也会随之增加,如果审计有多个子公司或分支机构的公司,审计师将用更多的时间去审计子公司和分支机构的财务报表,以及公司的合并报表,这也将增加他们的审计费用;徐琪[3]研究发现审计费用与公司面临的经营风险存在正相关关系,即公司负债率较高,则潜在的风险越大,审计师需要花费更多的精力,审计费用也会增加;吉小月等[4]认为公司盈余管理的动机让审计师面临的诉讼风险增加,这样也会增加其审计费用.盈余管理的一个动机是管理者通过应计利润来掩盖公司的不良业绩,把未来的费用提前确认,而将部分收益提前确认或是将某一部分良好的业绩推迟到以后的年份;另一个动机是通过增加财务报表的净利润,从而来增加公司的股票价值与公司的市场价值.
在事务所层面,张爱华[2]认为在激烈的市场竞争中,通常会产生级差效应,即事务所为了提供高质量的审计服务,高级差比低级差的会付出更高的审计成本,与此同时也会要求得到更高的审计利润作为回报.因此,人们普遍认为,规模越大,拥有优秀的审计人才越多的会计事务所,所提供的服务质量越高,获得公众的信任也就更容易,相应的审计费用也就增加;吉小月等[4]在分析审计收费的影响因素的基础上,根据审计对象的特点和审计对象,分析后认为事务所审计质量与其品牌呈正相关,也就是说品牌越好,审计质量也就越高,费用也就越高;魏振认为审计师变更将导致审计费用降低,而在国内市场上,初次审计中存在“审计定价折扣”现象;李明辉[5]发现事务所合并行为会影响审计费用.
国内文献更多地关注审计收费的影响因素,但对审计收费出现异常的情况没有给予足够的重视.但也有部分专家通过审计费用的降低和增加,发现了审计收费异常的现象.如陈炜煜等[6]认为审计费用的提高和审计意见购买之间呈显著负相关,相反则呈显著正相关.当上市公司上一年被出具非标准审计意见时,就会通过向当前或下一任的审计师提出增加审计费用的方式,进行审计意见购买.当企业不能够购买意见时,就会通过降低审计费用来对会计事务所进行报复;蔡春等[7]认为如果公司里的高管曾有过审计经历则可能有能力与动机实施盈余管理.如果审计师没有发现公司实施盈余管理来操纵利润,则可能会低估公司的风险,并降低了相应的审计成本.而与会计师事务所的高管有关联的公司也可以依靠其更专业的财务知识和技能,更准确的职业判断能力、更好的沟通技巧和更多的审计经验,加之利用其相互交织的关系网络等达到所需要的效果.隐性盈余管理行为通常较为隐蔽,审计风险可能不足以降低审计收费;唐跃军[8]研究发现事务所规模也是影响到审计意见和异常审计收费之间的关系的因素.一般来讲,公司管理层会更愿意向规模较小的事务所付出异常的审计费用,以购买较好的审计意见.
2 假设及模型设计
2.1 提出假设
根据国内现有文献关于审计收费与异常审计收费的研究成果[9-20],本文提出以下两个假设:
假设1:审计师变更与异常审计收费之间存在负相关关系.根据文献中提出,国内的审计市场存在着“审计定价折扣”现象,即审计师变更导致后一任审计师收取的审计费用低于前一任审计师.
假设2:审计师变更与异常审计收费之间存在正相关关系.
2.2 模型设计
2.2.1 确定异常审计费用的设计
(1)异常审计费用的线性回归模型
目前有两种理论方法可以帮助我们确定异常审计费用.第一种是基于资产规模,采用线性回归方法建立预期的审计成本模型,异常审计费用用回归残差表示;二是通过计算年度审计费用变化,并用年度变动值表示异常审计费用.文中采用线性回归方法计算异常审计费用.即提出建立模型:FEE=β0+β1×ASSET+ε,其中FEE表示审计费用,ASSET表示企业总资产.
本文通过巨潮资讯网收集2013年—2015年三年沪市A股上市公司的财务数据和审计收费相关数据,并实施以下筛选程序:不包括年度信息不完整的上市公司数据;剔除同时发行B股和H股的上市公司;剔除指标异常的上市公司.最终样本数为2 892个.
首先运用软件SPSS17.0进行线性回归,选取2013、2014和2015连续三年沪市上市公司数据作为研究样本,对正常审计收费进行回归分析,结果见表1.
从回归结果来看,F统计量为5 638.641,p=0.000,说明审计费用与资产规模之间存在显著的线性关系,概率为100%.调整后的R方等于0.661,拟合度很好,可以解释审计收费66.1%的变化.D-W统计量取值1.861,比较接近2,说明残差之间相关性不明显.获得审计费用和总资产的关系模型:FEE=1 397 804.425+(6.652E-6)×ASSET,利用此模型,即可计算获得正常的审计费用.
表1 正常审计费用的线性回归

模型回归系数T值Sig.常数项1 397 804.42512.0540.000资产6.652E-675.0910.000F值5 638.641(Sig.为0.000)R方0.661Durbin-Watson1.841
(2)异常审计费用的浮动限度
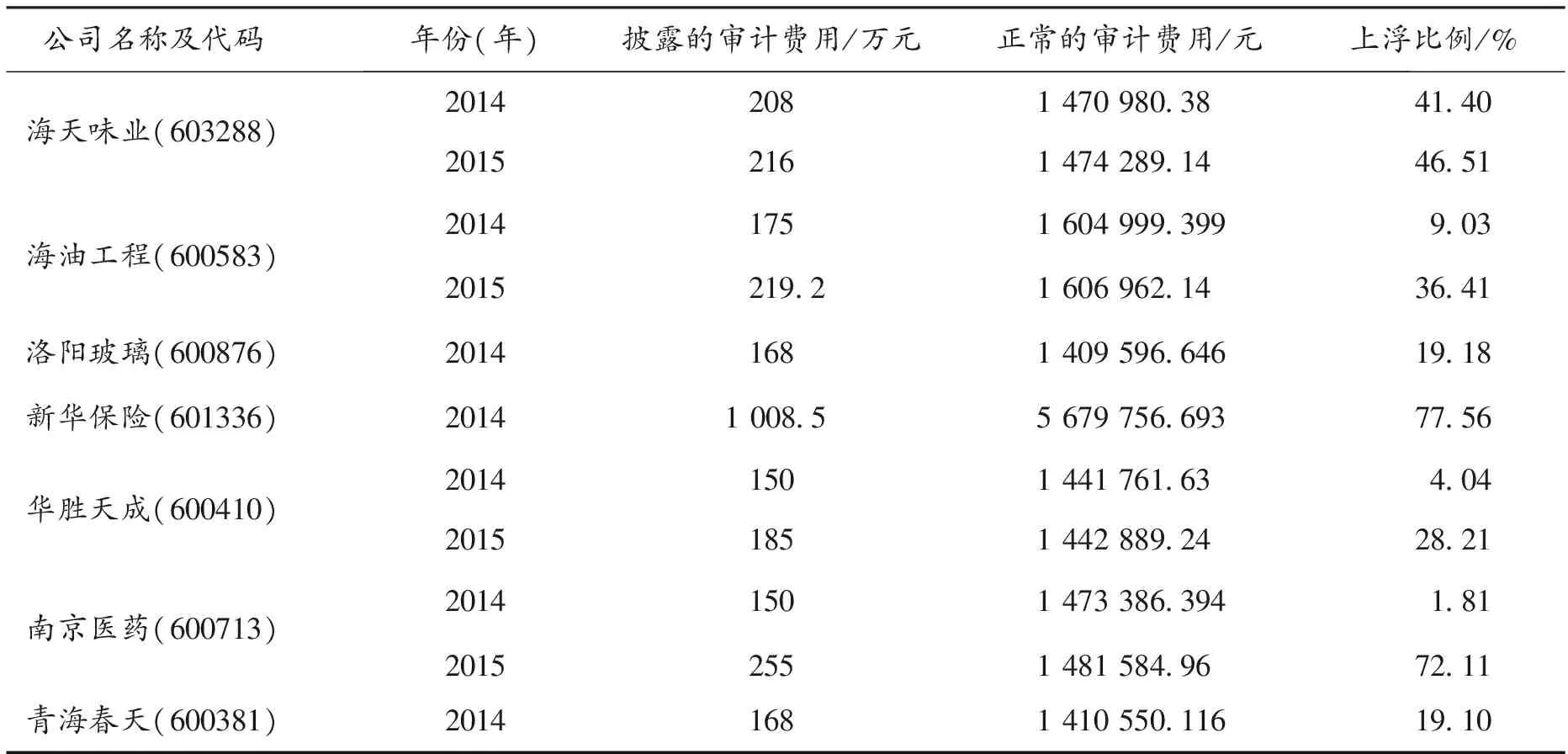
确定正向的异常审计费用,计算正常审计费用浮动上限.2013年—2015年来沪市A股有7家上市公司(见表2)被曝光审计费用高于正常审计费用的.通过计算平均值,发现实际审计费用平均高于正常审计费用的32.31%,因为浮动上限是平均水平,因此制定的浮动上限应略低于32.31%,故正常审计费用的浮动上限定为上浮30%.也就是说,审计费用比正常审计费用高30%以上,则该审计费用被视为正向的异常审计费用.
确定负向的异常审计费用,并计算正常审计费用浮动下限.2013年-2015年来沪市A股有8家上市公司(见表3)被曝光审计费用低于正常审计费用.通过计算平均值,发现实际审计费用平均低于正常审计费用30.09%,因此制定的浮动下限应略低于30.09%,故正常审计费用的浮动下限定为下浮30%.也就是说,如果审计费用比正常审计费用低30%以上,则该审计费用被视为负向的异常审计费用.
表2 正常审计费用的浮动上限
公司名称及代码 年份(年)披露的审计费用/万元正常的审计费用/元上浮比例/%海天味业(603288)2014208 1 470 980.3841.40 2015216 1 474 289.1446.51 海油工程(600583)2014175 1 604 999.3999.03 2015 219.2 1 606 962.1436.41 洛阳玻璃(600876)2014168 1 409 596.64619.18 新华保险(601336)2014 1 008.5 5 679 756.69377.56 华胜天成(600410)2014150 1 441 761.634.04 2015185 1 442 889.2428.21 南京医药(600713)2014150 1 473 386.3941.81 2015255 1 481 584.9672.11 青海春天(600381)2014168 1 410 550.11619.10
2.2.2 数据来源与筛选
本文通过巨潮资讯网手工收集2016年沪市A股上市公司的财务数据和审计相关数据,并实施以下筛选程序:不包括年度信息不完整的上市公司数据;剔除同时发行B股和H股的上市公司;剔除指标异常的上市公司.最终样本数为1 071个.
2.2.3 变量定义
见表4
2.2.4 模型构建
为了验证假设,需衡量异常审计费用与是否变更事务所.本文构建的模型如下:
Ref=β0+β1Change+β2Big4+β3Opn+β4Emg+β5Se+β6Re+β7In+β8Cata +β9Cr+β10Lev+β11Ro+ε.
其中,β0为常数项,β1-β11为回归系数,ε为残差项.
表3 正常审计费用的浮动下限

公司名称及代码年份(年)披露的审计费用/万元正常的审计费用/元下浮比例/%海天味业(603288)20131 38 1 442 520-4.33 ∗ST兴业(600603)201345 1 400 275-67.86 迪马股份(600565)2013140 1 527 434-8.34 天津磁卡(600800)201450 1 402 905.113-64.36 华光股份(600475)2014120 1 427 792.673-15.95 201571.6 1 431 516.03-49.98 通威股份(600438)2014110 1 438 909.067-23.55 洛阳玻璃(600876)2015120 1 406 545.39-14.68 青海青天(600381)201568 1 411 860.00-51.84
表4 变量的定义

变量类型变量 变量解释因变量Ref表示异常审计费用,本文用自然对数表示自变量Change事务所变更,当发生变更,为1,否则为0控制变量Big4当事务所为“四大”时,为1,否则为0Opn审计意见,出具非标准意见为1,否则为0Emg盈余管理,上年度亏损时,为1,否则为0Se表示公司规模,本文用总资产的自然对数表示Re应收账款水平,应收账款除以总资产表示In存货水平,存货除以总资产Cata流动资产与总资产之比,用流动资产除以总资产表示Cr流动比率,用流动资产除以流动负债计算Lev财务杠杆,用资产负债率表示Ro盈利能力,用总资产收益率表示
3 实证检验分析
3.1 描述性统计分析
由表5中可以看出,异常审计费用最小值为12.122 4,最大值为17.758 6,标准差为0.897 2,事务所变更的标准差为0.284.其他变量中,流动比率的差异性较大,最小值为0.077 6,最大值为26.653 3, 标准差为2.197 5. 公司规模最小值为17.778 5,最大值为29.744 2,标准差为1.583 3.盈利能力最小值为-1.033 5,最大值为0.578 0,标准差为0.081 5.
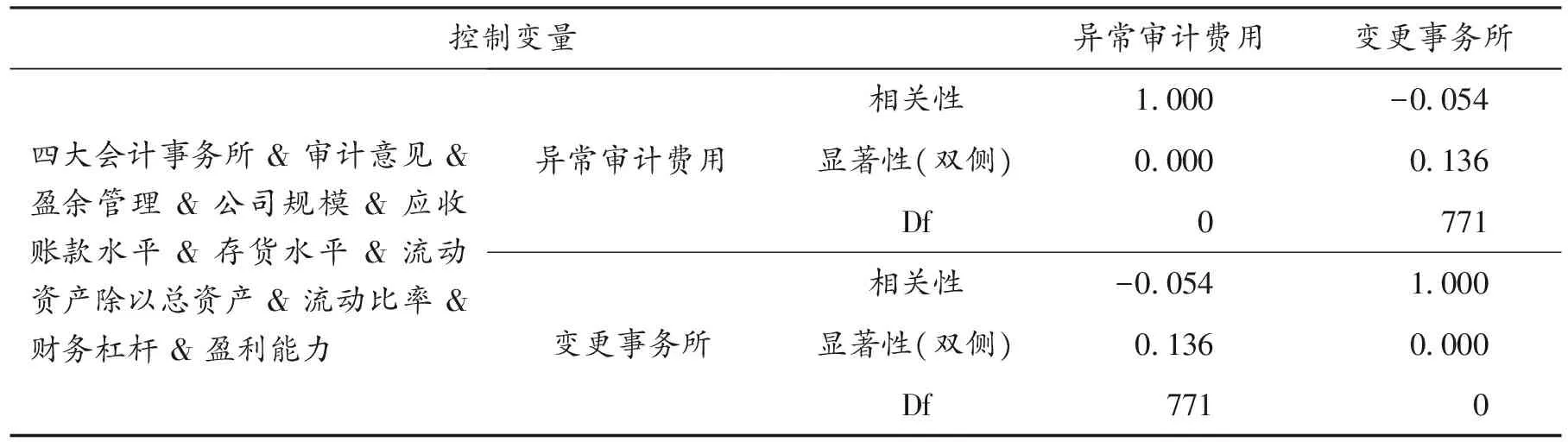
3.2 相关性分析
表6是变量之间相关性分析结果,从中可以看出异常审计费用作为因变量,审计师变更作为自变量,其余变量作为控制变量.由表6可以看出,异常审计费用与变更事务所之间存在负相关关系.
表5 描述统计分析表

N极小值极大值均值标准差异常审计费用78312.122 417.758 613.689 1730.897 180 1变更事务所7830 1 0.09 0.284 四大会计事务所7830 1 0.10 0.294 审计意见7830 1 0.05 0.220 盈余管理7830 1 0.14 0.348 公司规模78317.778 529.744 222.540 0171.583 283 2应收账款水平7830.000 01.115 10.093 6180.108 491 0存货水平7830.000 04.000 00.155 9510.210 466 4流动资产除以总资产7830.007 32.836 10.540 3220.244 948 6流动比率7830.077 626.653 32.080 6622.197 533 2财务杠杆7830.005 51.476 30.464 9460.219 871 1盈利能力783-1.033 50.578 00.028 6100.081 469 0有效的 N (列表状态)783
3.3 回归分析
表6 相关性分析
控制变量 异常审计费用变更事务所四大会计事务所 & 审计意见 & 盈余管理 & 公司规模 & 应收账款水平 & 存货水平 & 流动资产除以总资产 & 流动比率 & 财务杠杆 & 盈利能力异常审计费用变更事务所相关性1.000 -0.054 显著性(双侧)0.000 0.136 Df0 771 相关性-0.054 1.000 显著性(双侧)0.136 0.000 Df771 0
表7 回归结果1

模型RR 方调整 R 方标准估计的误差Durbin-Watson10.812a0.6600.6550.526 870 51.393a. 预测变量: (常量), 盈利能力, 存货水平, 应收账款水平, 四大会计事务所, 变更事务所, 流动比率, 盈余管理, 审计意见, 公司规模, 流动资产除以总资产, 财务杠杆.b. 因变量: 异常审计费用
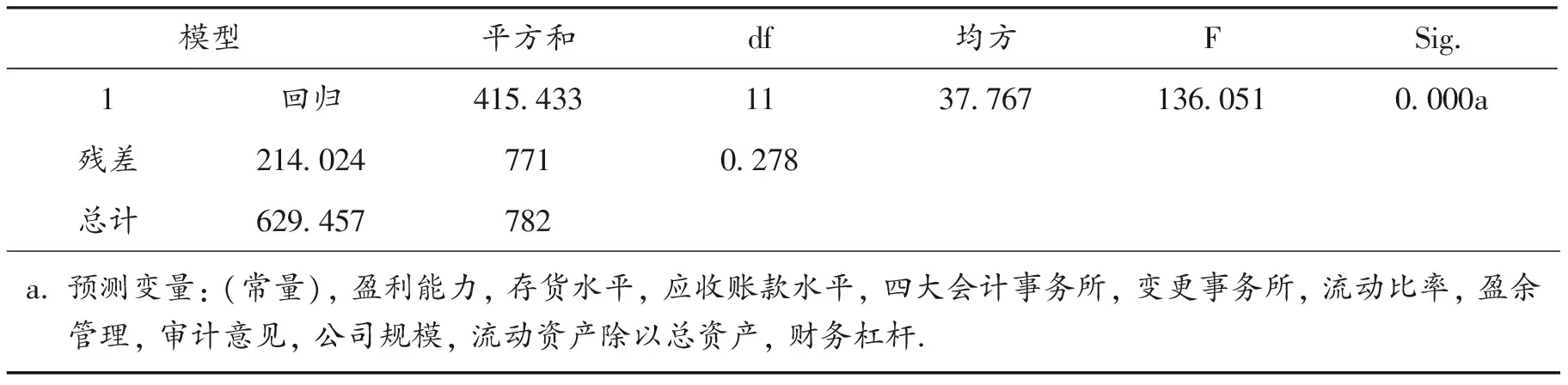
表8 回归结果2
模型平方和df均方FSig.1回归415.4331137.767136.0510.000a残差214.0247710.278总计629.457782a. 预测变量: (常量), 盈利能力, 存货水平, 应收账款水平, 四大会计事务所, 变更事务所, 流动比率, 盈余管理, 审计意见, 公司规模, 流动资产除以总资产, 财务杠杆.
表9 回归结果3

模 型 非标准化系数 标准系数B标准 误差试用版tSig.(常量)5.1490.34714.8210.000变更事务所-0.1000.067-0.032-1.4920.136四大会计事务所0.8510.0740.27911.5600.000审计意见0.2450.0980.0602.5040.012盈余管理0.0250.0590.0100.4210.674公司规模0.3780.0160.66723.9680.000应收账款水平0.4110.2110.0501.9510.051存货水平-0.2260.104-0.053-2.1660.031流动资产除以总资产0.0240.1080.0070.2220.824流动比率-0.0050.011-0.011-0.4050.686财务杠杆-0.1320.125-0.032-1.0570.291盈利能力-0.4490.263-0.041-1.7080.088a. 因变量: 异常审计费用
为了验证本文的假设,根据回归模型进行回归,得出表7、表8、表9.从以上回归结果来看,F统计量为136.051,p=0.000,概率为100%说明变量之间存在显著的线性关系.调整后的R方等于0.655,拟合程度很好,可以解释异常审计收费变化的66%.D-W统计量取值1.393,较为接近2,可见残差之间没有明显的相关性.得到回归方程:Ref=5.149+(-0.1)×Change+0.851×Big4+0.245×Opn+0.025×Emg +0.378×Se+0.411×Re+(-0.226)×In +(0.024)×Cata+(-0.005)×Cr+(-0.132)×Lev+(-0.449)×Ro.
可以看出,审计师变更是为异常审计费用的反向指标,表示审计师变更增长1%,异常审计费用下降10%,这也证实了本文的假设1,即审计师变更与异常审计收费呈负相关关系.
控制变量中,存货水平、财务杠杆、盈利能力均与审计费用呈负相关关系;Big4的回归系数为正且显著;公司规模与异常审计费用呈正相关关系且显著.
4 结论
本文研究了审计师变更对异常审计收费的影响和异常,并使用2013年—2015年上海证券交易所的上市公司数据,借鉴许良虎[9]、周小愈[10]等建立的异常审计费用模型,结合我国沪市上市公司异常审计费用的现状,推出我国上市公司异常审计费用的浮动的上下限.再考虑异常审计费用的影响因素,并提出审计师变更与异常审计费用有相关关系,并结合2016年沪市上市公司的数据,建立模型并验证审计师变更与异常审计费用存在负相关关系,这表明审计师的变更会相应的减少异常审计费用现象存在,并会在一定程度上对审计报告的可信度进一步加强.
当然,在本文的研究中也有一些局限性.由于一些数据的获取困难,以及尚有一些异常审计费用的影响因素没有考虑进来,也可能削弱本文的结论.
