U(1)自旋交换下的一维关联电子体系的相图∗
2019-12-04丁汉芹张军
丁汉芹,张军
(1.新疆大学物理科学与技术学院,新疆 乌鲁木齐 830046;2.新疆大学理论物理中心,新疆 乌鲁木齐 830046;)
0 引言
凝聚态物理中的一维关联电子体系是个非常重要的研究课题.一方面,在理论上一维问题比相应的高维情况容易分析,有些情况下甚至有精确解.从一维问题中获得的结果为理解高维问题提供重要的数据,如二维铜氧化物的超导机制[1],而且一维模型能描述很多实际存在的准一维材料的性质,如有机导体[2].另一方面,一维体系在实验中也可以制备出来,如碳纳米管[3],量子线[4].尤其当前光晶格中超冷原子费米气的实现,这使得人们通过可控的方式研究多体相互作用[5,6],极大提高了人们对一维相互作用电子体系的研究兴趣.但是一维体系中的电子因其相空间极度受制而表现为高度关联的,Hubbard模型和其相应的扩展模型成为描述电子关联的重要理论手段[7].因其在低维体系方面可能的应用和丰富的基态结构,广泛研究的是包含在位电子和最近邻电子库仑作用的扩展Hubbard模型,即通常所说的t-U-V模型.长期以来,很多研究致力于对其基态特性的理解.即便如此,t-U-V模型的相图仍然存在着争议,分歧集中在键序电荷密度波(BOW)的存在问题.在该模型的早期工作中,BOW相并没有出现,直到Nakamuru第一次报道:从弱耦合到中间耦合排斥区域,这个相存在U ≃2V 位置附近,夹在自旋密度波(SDW)相和电荷密度波(CDW)相[8]之间.随后一系列研究证实了这个二聚化相的存在[9−16].但对此也存在着不同的观点,Jeckemann等人认为BOW相只是存在CDW-SDW边界上一段短的碎片上[17],Zhang[18]和Deng[19]等人的研究宣称BOW相是不存在的.尽管如此,大多数研究还是赞成BOW相的存在,但其中很少研究解释BOW相存在的原因,而且给出的解释也不一样.由此可见,进一步研究一维扩展Hubbard模型的基态还是很有必要的.
另一方面,传统的t-U-V模型仅仅描述了各向同性的电子,即SU(2)自旋交换型的,库仑作用V假定与内禀自旋无关.因此,得到的SDW 实际上是自旋三分量简并的临界态.在这种情况下,一个有趣的问题出现了:如果涉及的电子是自旋各向异性的,模型的基态相图会是怎么样的?如果情况果真如此,那么相互作用V将会与自旋有关.从物理上来说,这样的各向异性可以来源于晶体的各向异性结构、自旋-轨道耦合等因素.同时,在t-U-V模型中人们并没有考虑最近邻电子间自旋交换作用(J).实际上,一维t-U-J模型也是广泛的研究着一种理论模型,如一维铁磁交换中的三相超导[20],一维反铁磁性交换中的有能隙的自旋液体[21]、铜氧化物中电荷转移[22].从相互作用角度来讲,近邻格点上电子的电荷库仑作用和自旋交换作用是可以同时存在的,并与V产生竞争作用.尤其对磁性关联电子体系来说,t-U-V-J模型更是个合适的候选者.在这篇文章中,我们考虑U(1)各向异性的相互作用,相应的哈密顿量定义为
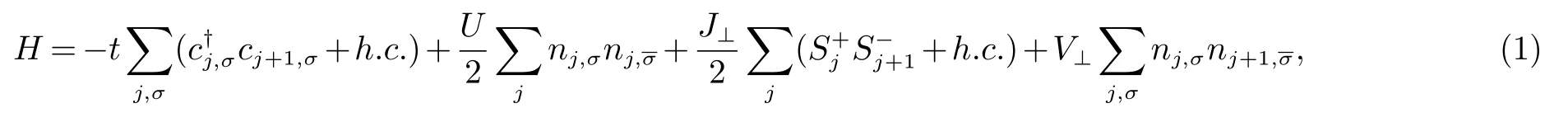
哈密顿量(1)描述着丰富的一维多体物理,在极限情况下能简化为特定的已知模型.没有最近邻作用的情况对应著名的Hubbard模型,半满填充和在位库仑排斥作用下,它的基态是临界自旋密度波的绝缘体.没有最近邻库仑作用(V⊥=0)的情况描述着横向自旋交换的扩展Hubbard模型,展现出丰富的基态相图[23].当不存在自旋交换作用时(J⊥=0),模型描述着自旋相反电子库仑作用的电子体系[24].在这篇文章中,我们考虑库仑作用和自旋作用竞争下的各向异性一维扩展Hubbard模型基态相图.我们只考虑半满情况,相关的倒逆过程可以存在.相互作用在弱耦合区域,以保证玻色化方法和重整化群分析能够有效运用.同时,相互作用属于物理上存在的情况,即电荷库仑作用是排斥的,自旋作用可以排斥(反铁磁)、也可以吸引(铁磁),而不考虑唯像情形(U,V⊥<0).研究结果表明,基态相图由四个不同的绝缘相组成:无自旋激发能隙的Mott绝缘体(MI)和Haldane绝缘体(HI)、有自旋激发能隙的自旋密度波(SDW)和键序自旋密度波(BSDW).
1 低能场理论分析
一维相互作用电子体系的场理论分析依赖于弱耦合方法,即模型参数满足|U|,|J⊥|,|V⊥|≪t.低能物理主要由费米点(±kF)附近的态描述,在半满下,kF=π/2a(a是晶格常数).相互作用的低能激发是费米点附近的粒子-空穴对激发,我们只需保留费米波矢kF的电子算符的傅里叶模式.这样我们可以将谱的色散关系进行线性变换,获得二支费米子,即左费米子ψLσ和右费米子ψRσ.同时利用连续极限,x=ja且a→0.在坐标表象下,这等价于变换这样的变换导致下列连续模型的哈密顿量
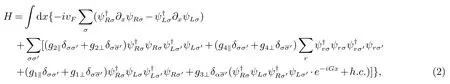
其中vF=2ta是费米速度.gi(i=1,2,3,4)是电子-电子耦合常数,在动量空间中它们分别描述后向散射(g1)、前向散射(g2,g4)和倒逆散射(g3)过程,它们对相同自旋和相反自旋(gi⊥)的电子散射可以有不同的振幅.G是倒格矢,由于准动量守恒的要求,只有满足G=4kF时,才会有这说明耦合相反自旋电子(泡利不相容原理的限制)的倒逆散射只能发生在电子半满填充下.原则上应该还有自旋平行的倒逆散射它是一个自旋-电荷耦合算符,但是在弱耦合区域和重整化下它具有较高的标度维数(d≃4),仅是一个强无关算符,因此可以像其他研究一样忽略其作用[20,25−29].
在一维电子体系中,由于自旋-电荷分离,低能激发有着独立的自旋模式和电荷模式.在这种情况下,分析(2)式描述的基态相图的一种有效工具是玻色化方法[30−32].利用这种技巧,费米场的手征分量能够通过电荷场和自旋场的互相对偶的玻色算符φν和θν(ν=c,s)顶角算符表示,
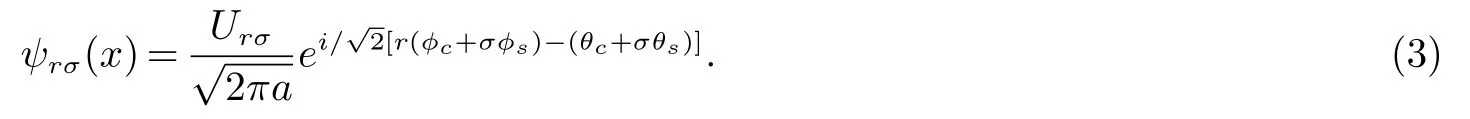
下指标r=L,R分别表示费米场的左、右支,分别对应指数中的r=−,+.同样,下指标σ=↑,↓也分别对应σ=−,+.场算符φc,θc和φs,θs分别描述集体电荷激发和集体自旋激发,并有对易关系
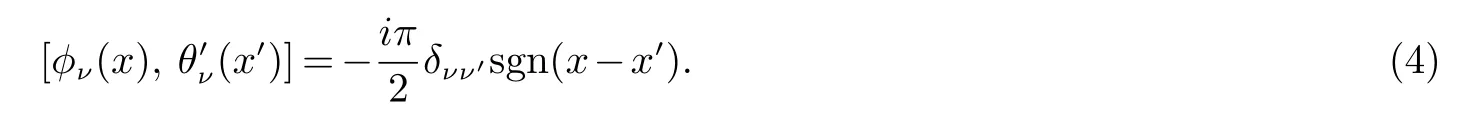
厄米算符克莱因子满足代数

以保证不同费米子算符的反对易关系.
这样,一维电子体系(1)的低能物理就由电荷场和自旋场的sine-Gordon理论描述,即哈密顿量可以重新写作H=Hc+Hs,其中,
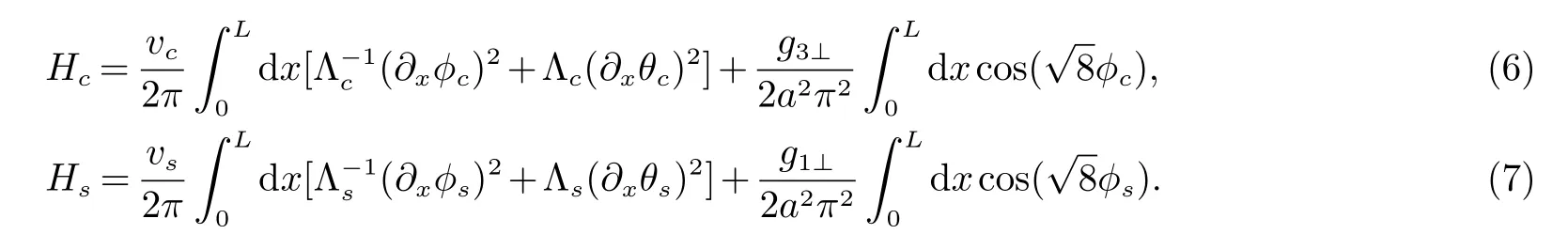
L是体系的长度,电荷、自旋元激发速度vν和高斯耦合常数Gν(ν=c,s)定义为
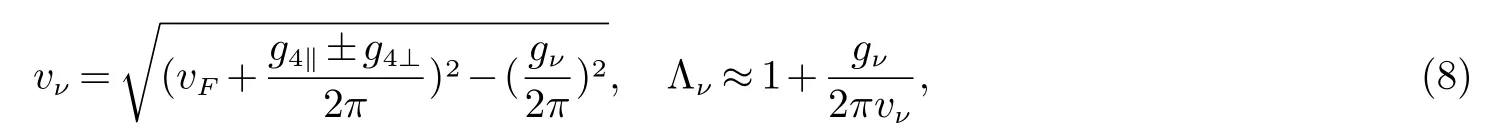

有效哈密顿量(6)和(7)包含二个非Tomonaga-Luttinger液体过程:倒逆散射(g3⊥)和后向散射(g1⊥).在电荷-自旋分离假设下,它们的相关性可以由重整化群分析来判定.在标度变换下:a →edla,l=lnL是标度长度,无量纲的跑动耦合常数的一环重整化群方程表示为[8]

以上标度方程中,yν0(0)=2(Λν−1),ycλ(0)=g3⊥/πvc,ysλ(0)=g1⊥/πvs.这对方程描述着电荷渠道和自旋渠道的K-T相变[33],重整化流向图如图1所示.从中看出,在yν0(0)≥|yνλ(0)|区域,yνλ(l →∞)→0,低能激发是无能隙的,∆ν=0,相场φν是个涨落场,不断振荡.这对应弱耦合区域(WC),倒逆散射和后向散射是无关过程,体系的基态属性完全由拉亭格液体理论描述.在相反的参数区域yν0(0)<|yνλ(0)|,yνλ(l →∞)→±∞,低能激发有能隙的,∆ν>0.随着增加的长度标度,重整化流标向强耦合区域(SC),倒逆散射和后向散射是相关过程.根据裸耦合g3⊥(g1⊥)是正还是负,相场钉扎在真空期望值
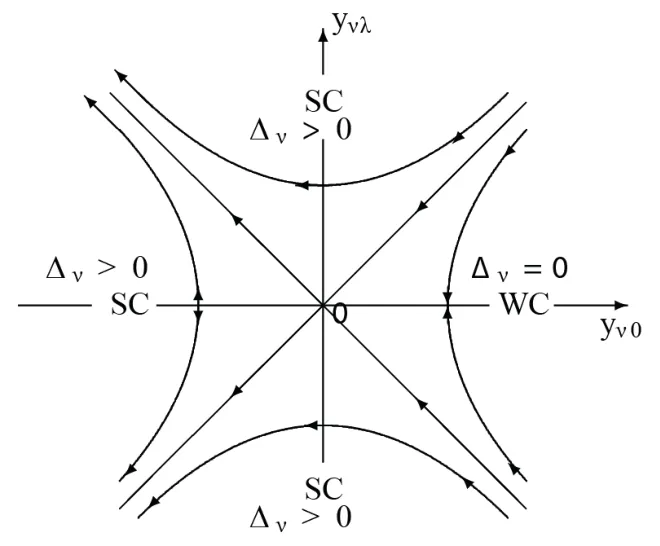
图1 重整化群流向图,箭头表示流向.WC和SC分别表示弱耦合和强耦合区域.∆ν =0表示电荷(自旋)激发无能隙,∆ν>0表示电荷(自旋)激发有能隙Fig 1 The renormalization-group flow diagram.The arrows represent the direction of flows with increasing length scale.WC and SC denote weak- and strong-coupling regimes,respectively.∆ν=0 indicates gapless excitations in the charge or spin channel,while ∆ν>0 gapped excitations
根据以上重整化群理论,我们可以分析量子相变.在低能电荷激发部分,由方程(9)和(10)可知,如果V⊥>0,总有gc

在U+J⊥−2V⊥>0 的区域,真空期望值在相反区域
对低能自旋激发而言,情况有所不同.由于gs和g1⊥的大小关系是任意的,所以存在自旋-激发能隙相变,对应相变线

在2V⊥+J⊥>0的区域,自旋激发没有能隙(∆s=0);在2V⊥+J⊥<0的区域,自旋激发有能隙(∆s>0),且有
2 弱耦合基态相图

表1 不同类型的相、序参量、相场的期望值和相应的玻色化形式Tab 1 Different type of dominant phase,order parameter,the average value of phase field and the corresponding bosonized version
我们通过计算序参量和关联函数来确定基态相图.由于电荷激发总是有能隙,我们只需引入描述绝缘相的密度波序.同时考虑到自旋U(1)对称性,序参量包含相关内容总结在表一中.对应的关联函数定义为[34]

其中i = CDW,SDWα,BOW,BSDWα,α = z,±.两支相变线(15)和(16)把基态相图分为不同的四个区域,如图2所示.
区域A: V⊥
区域B: −J⊥/2
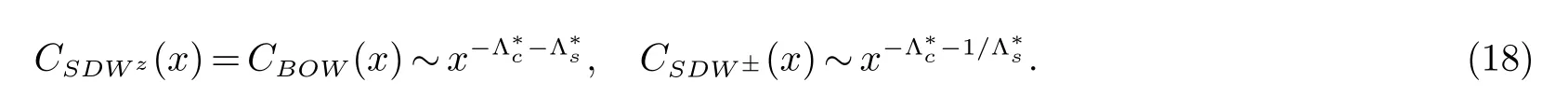
区域C: (J⊥+U)/2
区域D: V⊥>max{(J⊥+U)/2;−J⊥/2},电荷激发有能隙,但自旋激发无能隙(∆c>0,∆s=0).在电荷部分,不动点电荷场在自旋部分,不动点自旋场φs振荡,是涨落场.通过表1计算可知,序参量OSDWz=OSDW±=OBOW=0,序参量OCDW,OBSDWz和OBSDW±可以同时取非零值.为了确定最终的基态相,我们比较相应的关联函数(不计对数修正),
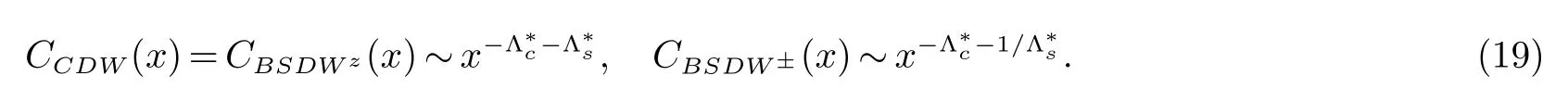
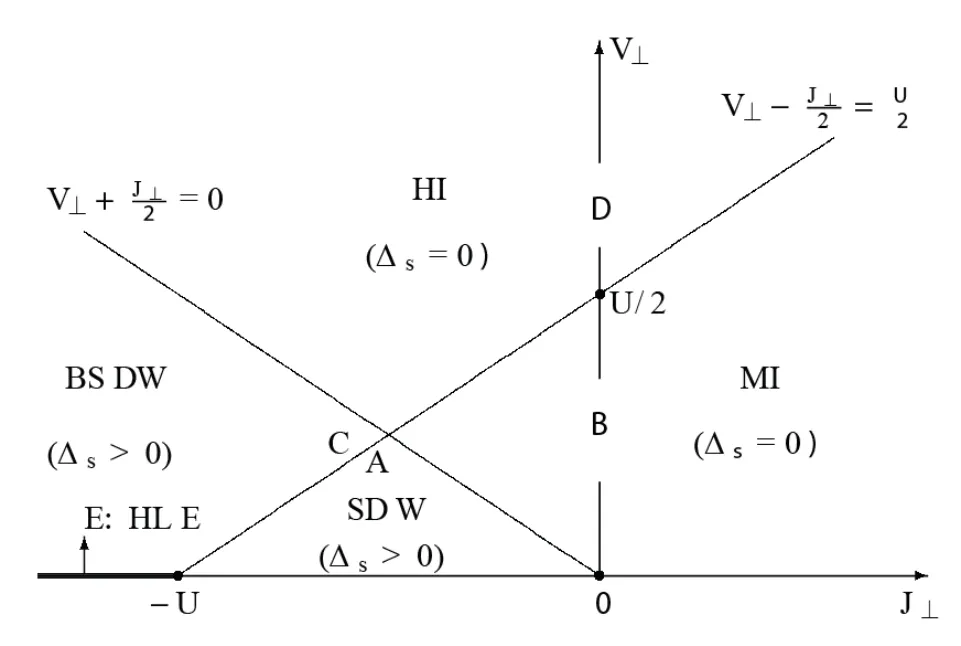
图2 半满下一维t-U-V⊥-J⊥模型的弱耦合基态相图.高斯相变线V⊥+J⊥/2=0 和自旋-能隙相变线V⊥−J⊥/2=U/2把相平面分为四个不同的相区Fig 2 The weak-coupling phase diagram of the 1D t-U-V⊥-J⊥model at half filling.The Gaussian transition V⊥+J⊥/2=0 and the spin-gap transition V⊥−J⊥/2=U/2 divide the plane into four phases.
3 结论
通过低能场理论方法我们研究了一维各向异性的扩展Hubbard模型,其中最近邻电荷库仑作用和自旋交换作用都与电子自旋有关,且是U(1)对称性的.在弱耦合区域,我们利用玻色化技术把费米体系转化为玻色场算符来表示.在自旋-电荷分离假设下,我们运用重整化群方法独立分析体系的低能电荷激发和自旋激发.在半满下,倒逆过程总是相关的,基态是绝缘体.在反铁磁交换区域,后向散射过程是无关的,低能自旋激发总是无能隙的,自旋-能隙相变发生在铁磁区域.高斯相变线2V⊥−J⊥=2U和自旋-能隙相变线2V⊥+J⊥=0把相图分为四个不同的相区.通过序参量和关联函数计算,我们得到了模型的基态相图,由SDW,BSDW,MI和HI组成.我们还发现,当V⊥排斥作用不存在时,在铁磁交换J⊥≤−U的区域,电荷激发能隙消失,BSDW相受到抑制,HLE金属相形成.同时,在基态中二个准长程序的绝缘相CDW和BOW 并没出现.研究结果揭示了各向异性的扩展Hubbard模型与各向同性的模型是不同的,各向异性的相互作用对体系的基态相图有着重要的影响.
