半群的区间值Q-模糊子半群∗

王丰效

(喀什大学数学与统计学院,新疆 喀什 844000)

0 引言

自从Zadeh[1]引入模糊集的概念以来,模糊集理论及其应用得到了迅猛的发展.Rosenfeld[2]首次提出模糊子群的概念,开创了模糊代数的新领域.作为模糊集的推广,区间值模糊集,直觉模糊集[3]等概念被提出,并被广泛应用于各类代数系统，取得了大量的研究成果[4−9].Kuroki将模糊集的概念应用于半群，提出模糊半群的概念，并讨论了半群的各类模糊理想[10].2001年,Jun[11]等给出了BCI-代数的Ω-模糊理想的概念,研究了它的相关性质.文献[12-14]分别讨论了BCI-代数的Ω- 模糊p- 理想的特性,BCH-代数的Ω-模糊点H-理想的性质,BCK-代数的Ω-模糊正定关联理想.文献[15]引入了半群的Ω-模糊子半群的概念,得到了它的相关性质.本文将Ω-模糊集与区间值模糊集相结合,给出了半群的区间值Q-模糊子半群的概念，讨论了区间值Q-模糊子半群的相关特征.

为了讨论方便,先给出一些相关概念.

定义1[8]设·是S的一个二元运算,如果对任意x,y ∈S有(1)x·y ∈S,(2)(x·y)·z=x·(y·z),则称(S,·)为一个半群.

为方便起见,二元运算x·y用xy表示.

定义2[8]设A是半群S的模糊集,如果对任意x,y ∈S有A(xy)≥A(x)∧A(y),则称A为S的模糊子半群.

非空集合X的区间值模糊集被定义为A=[AL,AU],这里AL和AU分别是X上的模糊集,并且对于任意x ∈X,有AL(x)≤AU(x),A=[AL,AU]是[0,1]的一个闭子区间.

若用D[0,1]表示区间数的集合.对D[0,1]中的两个元素可以定义加细极小（记为γmin）和加细极大（记为γmax）,也可以规定大小.D[0,1]中元素D1=[a1,a2],D2=[b1,b2],规定

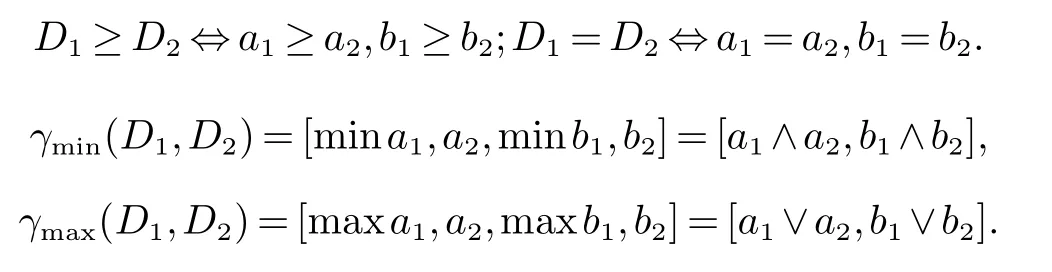
由D[0,1]中两个元素的大小规定以及加细极小和加细极大的定义可知,D[0,1]关于加细极小和加细极大构成完备格.

定义3[5]假设(S,·)为一个半群,A = [AL,AU]是S上的区间值模糊集,如果对于任意x,y ∈S有A(xy) ≥γmin(A(x),A(y)),则称A=[AL,AU]为半群S的区间值模糊子半群.如果对于任意x,y ∈S有A(xy)≤γmax(A(x),A(y)),则称A=[AL,AU]为半群S的区间值反模糊子半群.

假设Q表示一个非空给定集合,S为半群,称µ:S×Q →[0,1]为S的Q-模糊集.

定义4[16]假设(S,·)为一个半群,µ为S的Q-模糊集.称µ为S的Q-模糊子半群,如果对任意的x,y ∈S,q ∈Q有µ(xy,q)≥µ(x,q)∧µ(y,q).

1 主要结果

定义5假设Q表示一个非空给定集合,S为半群.A=[µA,νA]是S上的区间值模糊集,如果µA和νA都是S上的Q-模糊集,则称A=[µA,νA]为S的区间值Q-模糊集.

定义6假设(S,·)为一个半群,A=[µA,νA]为S的区间值Q-模糊集.如果对任意的x,y ∈S,q ∈Q 有A(xy,q)≥γmin(A(x,q),A(y,q)).则称A为S的区间值Q-模糊子半群.

例1设S={a,b,c},S上的二元运算如下表：

则(S,·)是半群.假设Q={q1,q2},定义S的区间值Q-模糊集A为

由定义可以验证A为S的区间值Q-模糊子半群.

由定义6可知,对任意的θ,记A+θ=[µA+θ,νA+θ]⊂D[0,1].如果A=[µA,νA]为S的区间值Q-模糊集,则A+θ也是S的区间值Q-模糊集.

定理1设A=[µA,νA]为S的区间值Q-模糊子半群,则A+θ也是S的区间值Q-模糊子半群.

定理2设A=[µA,νA]为S的区间值Q-模糊集,A=[µA,νA]为S的区间值Q-模糊子半群当且仅当µA和νA都是S的Q-模糊子半群.

证明(必要性)设A为S的区间值Q-模糊子半群,则对任意的x,y ∈S,q ∈Q有

即

因此µA(xy,q)≥µA(x,q)∧µA(x,q),νA(xy,q)≥νA(x,q)∧νA(x,q).故由定义4可得µA和νA都是S的Q-模糊子半群.

(充分性)如果µA和νA都是S的Q-模糊子半群,则对任意x,y ∈S,q ∈Q,有

因此

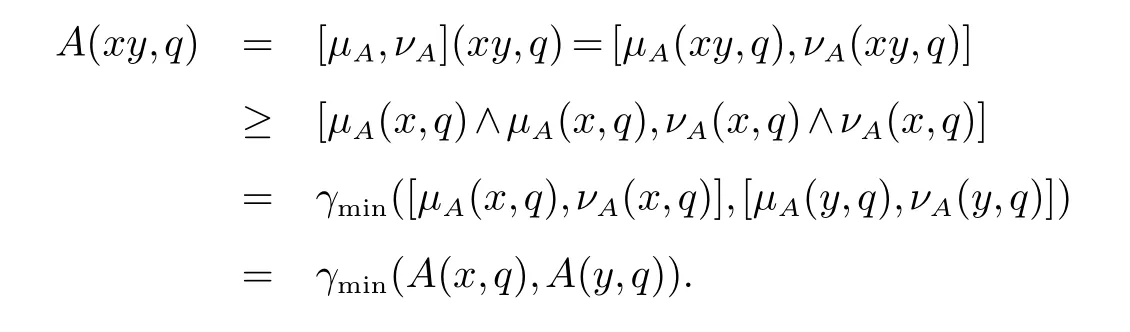
即A(xy,q)≤γmax(A(x,q),A(y,q)),所以A=[µA,νA]为S的区间值Q-模糊子半群.

推论1设A=[µA,νA]和B=[µB,νB]是S的区间值Q-模糊子半群,则[µA,µB]和[νA,νB]都是S的区间值Q-模糊子半群.

定理3设A和B都是S的区间值Q-模糊子半群,则A∩B 是S的区间值Q-模糊子半群.

证明由于A和B都是S的区间值Q-模糊子半群,故对任意x,y ∈S,q ∈Q,有

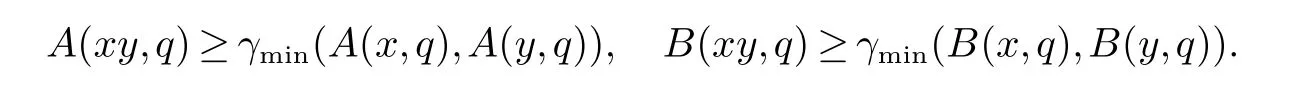
从而

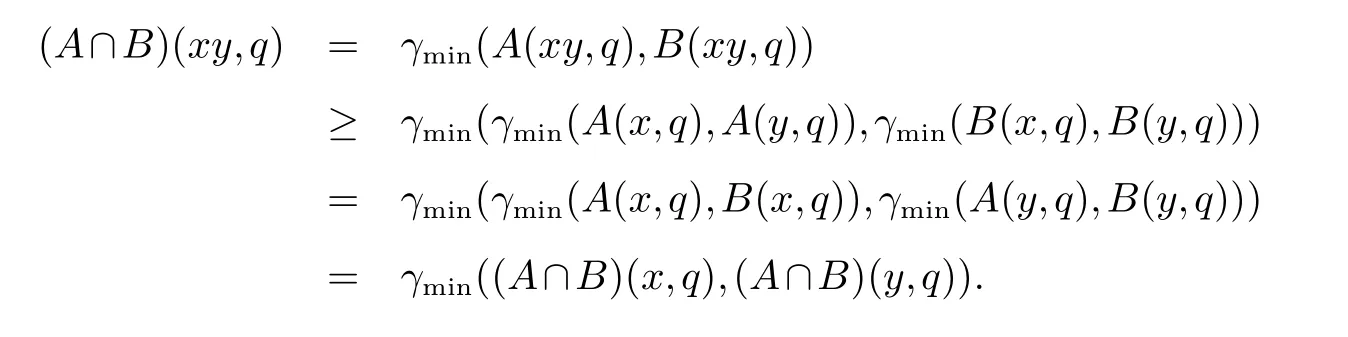
因此由定义2可知,A∩B 是S的区间值Q-模糊子半群.

如果给定集合Q是单元素集合,则S的区间值Q-模糊集就成为S的区间值模糊集,从而可得下面的几个推论.

推论2设A=[µA,νA]为S的区间值模糊集,A=[µA,νA]为S的区间值模糊子半群当且仅当µA和νA都是S的模糊子半群.

推论3设A和B都是S的区间值模糊子半群,则A∩B=γmin(A,B)是S的区间值模糊子半群.

定义7假设A=[µA,νA]为S的区间值Q-模糊集,称A[s,t]={x ∈S|A(x,q)≥[s,t],q ∈Q}为S的[s,t]上水平截集,称[s,t]={x ∈S|A(x,q)>[s,t],q ∈Q}为S的[s,t]强上水平截集,其中[s,t]⊂D[0,1].

定理4设A为S的区间值Q-模糊集,则A是S的区间值Q-模糊子半群当且仅当非空集A[s,t]是S的子半群.

证明(必要性)设A[s,t]非空,且x,y ∈A[s,t],则对任意q ∈Q,有A(x,q)≥[s,t],A(y,q)≥[s,t].由于A是S的区间值Q-模糊子半群,故对任意x,y ∈S,q ∈Q有

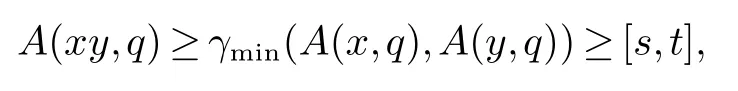
因此xy ∈A[s,t],从而A[s,t]是S的子半群.

(充分性)若A[s,t]是S的子半群,如果存在x,y ∈S,q ∈Q,使得A(xy,q)<γmin(A(x,q),A(y,q)),取区间[a,b]⊂D[0,1]满足A(xy,q)<[a,b]<γmin(A(x,q),A(y,q)),则A(x,q)>[a,b],A(y,q)>[a,b],A(xy,q)<[a,b].由于A[s,t]是S的子半群,从而x,y ∈A[s,t],即xy ∈A[s,t]与xy /∈A[s,t]矛盾.因此对任意x,y ∈S,q ∈Q,有A(xy,q)≥γmin(A(x,q),A(y,q)).因此A是S的区间值Q-模糊子半群.

定理5设A为S的区间值Q-模糊集,则A是S的区间值Q-模糊子半群当且仅当非空集[s,t]是S的子半群.

定理6设A为半群S的区间值Q-模糊子半群,则非空集U={x ∈S|A(x,q)=[1,1],q ∈Q}是S的子半群.

证明设U ={x ∈S|A(x,q)=[1,1],q ∈Q}非空,且x,y ∈U,则A(x,q)=A(y,q)=[1,1].由于A为S的区间值Q-模糊子半群,因而A(xy,q)≥γmin(A(x,q),A(y,q))=[1,1],即A(xy,q)=[1,1],从而xy ∈U,即U是S的子半群.

假设I是半群S的子集,定义S的区间值Q-模糊集AI满足：若x ∈I,AI(x,q)=[1,1]; 若x/∈I,AI(x,q)=[0,0].

定理7AI是半群S的区间值Q-模糊子半群当且仅当I是半群S的子半群.

证明设x,y ∈I,则AI(x,q)=[1,1],AI(y,q)=[1,1].由于AI是半群S的区间值Q-模糊子半群,从而AI(xy,q)≥γmin(AI(x,q),AI(y,q))=[1,1],即AI(xy,q)=[1,1],从而xy ∈I,即I是S的子半群.

假设I是S的子半群.下证AI是半群S的区间值Q-模糊子半群.对任意x,y ∈S,q ∈Q,分下面几种情况：

(1) 如果x,y ∈I,I是S的子半群,则xy ∈I,从而AI(xy,q) = (AI(x,q) = AI(y,q)) = [1,1],即有AI(xy,q) ≥γmin(AI(x,q),AI(y,q)).

(2) 如果x/∈I或y /∈I,则AI(x,q)=[0,0]或AI(y,q)=[0,0],故

故AI是半群S的区间值Q-模糊子半群.

引理1[15]设S和R是两个半群,f是S →R的同态满射.如果µ为半群S的Q-值模糊子半群,则f(µ) 为半群R的Q-模糊子半群.其中f(µ)=sup{µ(x,q)|f(x)=y}.

定理8设S和R是两个半群,f是S →R的同态满射.如果A为半群S的区间值Q-模糊子半群,则f(A)为半群R的区间值Q-模糊子半群.其中f(A)=γmax{A(x,q)|f(x)=y}.

证明由于A = [µA,νA]为半群S的区间值Q-模糊子半群,从而由定理1可得µA和νA都是S的Q-模糊子半群.记µf(A)=sup{µA(x,q)|f(x)=y},νf(A)=sup{νA(x,q)|f(x)=y}.根据引理1 可知µf(A)和νf(A)都是半群R的Q-模糊子半群.故由定理1可得f(A)=[µf(A),νf(A)]是半群R的区间值Q-模糊子半群.

定理9设S和R是两个半群,f是S →R的同态满射.若B =[µB,νB]为半群R的区间值Q-模糊集,则B为半群R的区间值Q-模糊子半群当且仅当f−1(B)为半群S的区间值Q-模糊子半群.其中f−1(B)=B(f(x),q).

证明(必要性)假设B为半群R的区间值Q-模糊子半群,则对于任意的x,y ∈S,q ∈Q,有

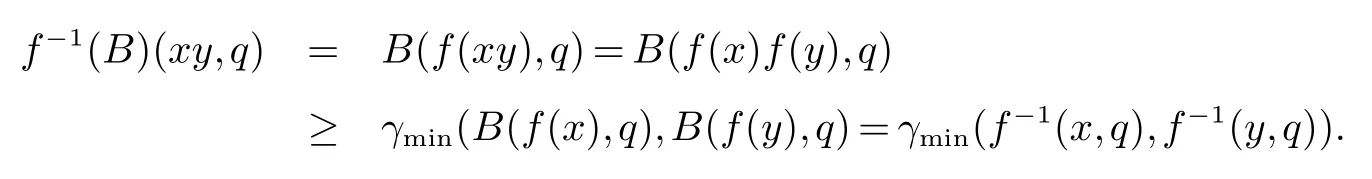
所以f−1(B)为半群S的区间值Q-模糊子半群.

(充分性)由于f是S →R的同态满射,因此对任意a,b ∈R,q ∈Q,存在x,y ∈S,使得f(x)=a,f(y)=b.于是

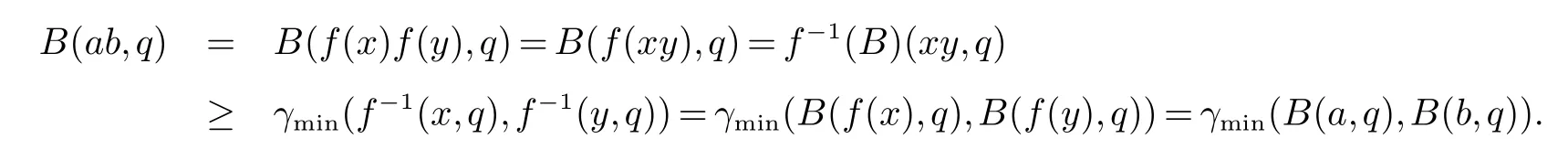
由定义6可知B为半群R的区间值Q-模糊子半群.

下面,我们讨论半群的区间值Q-模糊子半群直积的性质.假设S和R是两个半群,A和B分别是S和R上的区间值Q-模糊集,定义S×R上的区间值Q- 模糊集A×B为

定理10假设A和B分别是S和R上的区间值Q-模糊子半群,则A×B是半群S×R的区间值Q-模糊子半群.

证明对于任意的(x1,y1),(x2,y2)∈S×R,q ∈Q有

由于A和B分别是半群S和R上的区间值Q-模糊子半群,因此

故

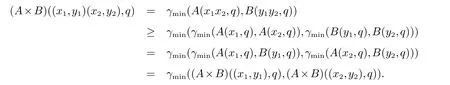
因此A×B是半群S×R的区间值Q-模糊子半群.

定理11假设A是半群S上的区间值Q-模糊子半群,则A×A是半群S×S的区间值Q-模糊子半群.

定理12设A是S上的区间值Q-模糊集,定义S上的区间值模糊集δA(x)=min{A(x,q)|q ∈Q}.如果A是S上的区间值Q-模糊子半群,则δA是S上的区间值模糊子半群.

证明设A是S的区间值Q-模糊子半群,对x,y ∈S,q ∈Q有A(xy,q)≥γmin(A(x,q),A(y,q)),因此

因此δA是S上的区间值模糊子半群.

定理13设A是S上的区间值Q-模糊集,对固定的q ∈Q,定义δq(x)=A(x,q).A是S上的区间值Q-模糊子半群当且仅当对任意固定的q ∈Q,δq是S上的区间值模糊子半群.

证明(必要性)设A是S的区间值Q-模糊子半群,则对于任意的x,y ∈S,q ∈Q,有A(xy,q)≥γmin(A(x,q),A(y,q)).因此对于固定的q ∈Q,有

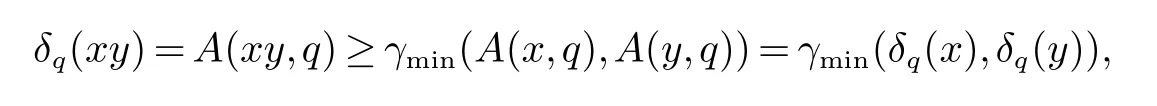
因此δq是S上的区间值模糊子半群.

(充分性)如果对于任意固定的q ∈Q,δq是S上的区间值模糊子半群.对于任意x,y ∈S都有δq(xy)≥γmin(δq(x),δq(y)),即A(xy,q)≥γmin(A(x,q),A(y,q)).因此A是S的区间值Q-模糊子半群.

命题1[15]若SQ表示从Q到半群S的映射的集合,在SQ上定义如下运算：对于任意的α,β ∈SQ,(α⊗β)(q)=α(q)β(q),q ∈Q,则SQ关于运算⊗构成一个半群.

定理14设A是半群S上的区间值模糊子半群，定义SQ的区间值Q-模糊集C:SQ×Q →D[0,1]满足C(α,q)=A(α(q)),则C是半群SQ的区间值Q-模糊子半群.

证明对于任意的α,β ∈SQ,q ∈Q,由于A是半群S上的区间值模糊子半群,从而有

所以C是半群SQ的区间值Q-模糊子半群.

定理15设M是半群SQ的子半群,则对任意q ∈Q,Mq={α(q)|α ∈M}是半群S的子半群.

证明由于M是半群SQ的子半群,因此对任意的α,β ∈M有α⊗β ∈M.进一步有α(q)∈Mq,β(q)∈Mq,α⊗β(q)∈Mq,故对任意q ∈Q,Mq={α(q)|α ∈M}是半群S的子半群.

如果Q是一个单元素集合,则区间值Q-模糊集就是通常的区间值模糊集,从上述结果可以看出,区间值Q-模糊集就是区间值模糊集的一种推广,相关的结论也是区间值模糊子半群相应结论的推广.

2 结论

本文将区间值模糊集与Ω-模糊集相结合,在半群中引入了半群的区间值Q-模糊子半群的概念,讨论了半群的区间值Q-模糊子半群的相关性质.给出了半群的区间值Q-模糊子半群与子半群,模糊子半群,区间值模糊子半群的关系.也讨论了半群的区间值Q-模糊子半群关于交运算的封闭性质,以及半群的区间值Q-模糊子半群的同态像和直积的相关性质.另外,区间值Q-模糊子集的概念也可以应用于其他代数系统.