一种实现流固实时交互的改进方法

唐 勇，高 虎，郭慧玲，3，赵 静，刘浩阳

1(燕山大学 信息科学与工程学院，河北 秦皇岛 066004)2(河北省计算机虚拟技术与系统集成重点实验室，河北 秦皇岛 066004)3(河北环境工程学院 信息工程系，河北 秦皇岛 066102)

1 引 言

流体模拟在游戏、影视特效、航空航天等方面应用广泛，并且一直是计算机图形学中的热门研究课题，但是流体运动形态变化多样，使得传统的欧式方法很难对其进行有效模拟；并且流固交互计算复杂，这使得流体与固体障碍物的交互模拟更具挑战性.

近年来，研究者们在流固交互模拟上做了大量的工作，不断推动计算机图形学领域的进步.2006年，Klingner等人[1]采用非结构化四面体网格模拟流体动画，这种方法能够很好地实现双向流体和刚体的交互，但在模拟效率上有所不足.随后，Batty等[2]提出一种快速变分框架来模拟流固耦合，在模拟性能上取得了较大的提升.2008年，Dobashi等人[3]提出了利用多个网格相互叠加的方法，实现了流体与网格物体的实时交互，但是局部网格大小的选择严重影响计算效率和交互效果.Matthias Müller等人[4]在2014年提出一种用于实时视觉效果的统一动态框架，这种方法使用统一的方式处理接触和碰撞，解决了传统基于粒子方法的常见问题.但是这种方法受固定粒径的限制，在流体和刚体间的交互模拟上有一定限制.2015年，邵绪强等人[5]将固体采样的边界粒子与动量守恒速度位置校正方案相结合，有效防止了流固边界面处的穿透现象.这种方法在当边界粒子的距离变得大于边界粒子的支撑半径时，速度位置校正方案不能很好地防止穿透.2016年，吕梦雅等人[6]基于物理的方法模拟了密闭空间中烟雾与障碍物交互，但是该实验只能完成烟雾与规则障碍物的交互.Ren等[7]提出了一种基于光滑粒子动力学(SPH)的方法，能够实现液体与气体间的转换，但是模拟出的气体运动缺乏层次感，导致效果不佳.同年，Weaver 和Xiao[8]发表了一篇关于SPH方法流体模拟的综述，详细分析了现有方法的优缺点及未来研究趋势.2017年，Hochstetter Hendrik和Andreas Kolb[9]利用SPH方法模拟流体的蒸发和冷凝，虽然具有很好的流体渲染细节，但是在蒸汽运动细节上稍有欠缺.同年，Jones和Southern[10]提出一种基于物理的模型模拟液滴间的相互作用，并应用到大型喷雾效应仿真中.2018年，Mashayekhi等人[11]提出一种分布式网格流体模拟系统，能够自动将较小的仿真拼接成一个独立的大型仿真，但是仿真效率较低.同年，Muzaffer等人[12]提出一种流固耦合的扩展分区方法，能够使用分区求解器进行求解，重用现有的求解器，提高了流固耦合效率，但是该方法忽略了流体的表面张力，具有一定的局限性.

综上，现有的流固交互模拟中，多数将固体边界表示成粒子的集合，这种方法一定程度上增加了模拟的计算量，降低了流固交互的效率.对此，引入柏林噪声函数以增加流体运动层次感，提出一种固体边界反作用力限制的新方法，旨在减小计算量的同时降低流体粒子穿透固体边界的可能性，从而实现流体与固体间的快速自由交互，同时考虑到流固交互时的碰撞效果，引入恢复系数，动态控制粒子与固体交互时的速度及动能恢复.

2 基于SPH方法的流体建模

目前常用的流体建模方法主要有两种，基于网格的欧拉方法和基于粒子的拉格朗日方法，两种方法都是通过求解流体力学方程(Navier-Stokes,N-S)来对流体进行建模.为了克服流体模拟中流体质量不易保持守恒、计算成本高等缺点，本研究采用一种无网格的完全拉格朗日方法——光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)方法.

2.1 建立N-S方程

不可压缩流体运动状态的描述主要包括质量守恒方程(公式(1))和动量守恒方程(公式(2))：

·u= 0

(1)

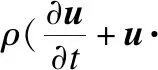
(2)

其中，u为流体速度，p为压力，ρ为密度，μ为运动粘滞系数，f为外力.

由公式(2)可知，想要利用N-S方程描述流体的运动规律，就必须对其各部分参数进行求解，为了减少计算成本，增大流体模拟效率，引入基于粒子的SPH方法.

2.2 基于SPH求解流体模型

SPH方法中将流体视为一个个分散的粒子，流体空间中任意点的属性值是由周围粒子叠加计算得到:

(3)

其中，Aj是要叠加计算的物理属性，mj和ρj是该点周围粒子的质量和密度，r是该点的位置矢量，W(r-rj,h)是半径为h的光滑核函数.

2.3 流体受力分析

由公式(2)可知，需要对密度ρ，压力p，粘滞力和外力f进行求解.

对于密度ρ，由公式(3)可得:

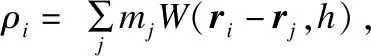
(4)

为了求解流体压强，引入理想气体状态方程，可得:

p=kρ

(5)

为了控制压强的耗散，对流体密度施加一个标准密度ρ0，可得:

(6)

当k和γ取不同的值时，会出现不同的视觉效果，这里取p=k(ρ-ρ0).

为了模拟真实流体的运动状态，需要计算流体粒子所受的压力和粘滞力，计算公式为:

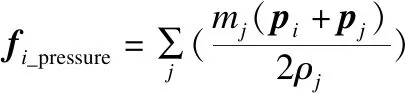
(7)

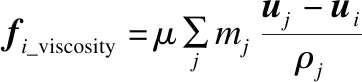
(8)

流体可分为液体和气体，为了增大方法的适用范围，同时使用本方法模拟气体和液体，对于气态流体，需考虑气体所在环境的浮力.浮力公式为:

fi_buoyancy=b(ρi-ρ0)g

(9)

2.4 引入柏林噪声的气态流体模型

通常情况下，采用SPH方法模拟气体时，粒子的速度和生命周期是一个固定值，这导致了模拟气体运动时缺乏运动层次感.为此，引入柏林噪声产生随机数值R=μPerlinNoise(t)(0μ1)的粒子速度和粒子生命周期，使气体运动模型更具层次感，增强模拟的真实感.

ui=ui·Noise(ri)

(10)

Ti=Ti·Noise(ri)

(11)

其中，ui为粒子i的速度，Ti为粒子的生命周期，Noise(ri)为关于位置ri处粒子速度或生命周期的柏林噪声函数.

3 流固交互处理

实际生活中，流体不仅要受到自身内力和外力的影响，还会和固体发生相互作用，因此实时模拟流体的运动规律极具挑战性.为了实时有效地处理流体与固体障碍物的交互，需要选用合适的时间积分方法和边界处理及碰撞计算方法.本研究采用计算量较小的蛙跳时间积分法获取模拟中流体粒子下一时刻的速度和位置；采用障碍物边界反作用力限制方法处理穿透问题,并通过改进发生碰撞时的粒子速度，以完成交互模拟.

3.1 蛙跳时间积分法 (Leap Frog)

蛙跳时间积分法具有包含显示速度项、计算量小等优势，选用蛙跳法有助于提高模拟实时性.

(12)

r(t+t)=r(t)+

(13)

(14)

最后可以利用平均数近似估计得到速度

(15)

式中，a表示粒子的加速度，r表示粒子的位置矢量，u表示速度，t为时间.

3.2 改进的固体边界模型

传统的固体边界模型采用的是虚粒子法[13]，这种方法在模拟时将固体边界看做粒子的集合，每个时间步都需要计算固体边界粒子的相关属性，从而产生大量的冗余计算，导致模拟实时性降低.此外，虚粒子方法对固体边界粒子和流体粒子的连续性方程和动量方程进行统一的计算，边界周围粒子不稳定，这导致了流体粒子会穿透固体边界的问题.

针对上述问题，本文引入一种固体边界反作用力限制的方法，通过网格对固体边界进行限定，然后在边界上施加一层反作用力区域，如图1所示.

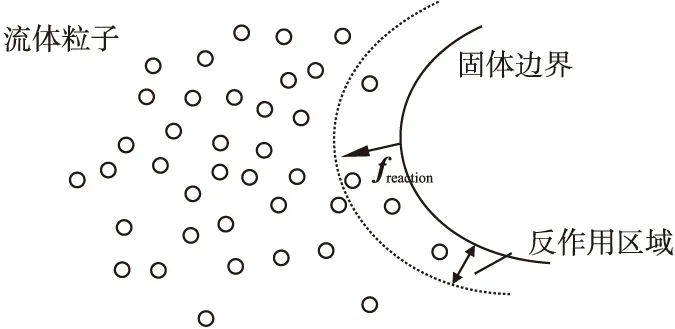
图1 固体边界反作用力模型Fig.1 Solid boundary reaction model

当粒子进入固体边界区域时，将受到这个力的作用，以实现流体与固体的自由交互，可以有效减小粒子发生穿透的可能性.即:

freaction= -ma

(16)

其中freaction为施加在固体边界上的反作用力；m为流体粒子质量；a为流体粒子加速度.

fi=kui

(17)

其中，fi为第i个流体粒子所受到的反作用力；k为关于反作用力大小的常数；ui为第i个流体粒子的速度.

3.3 流体与固体的交互处理

流体与固体交互时有一个相互作用的力，传统的交互方式忽略了流体与固体相互作用时所受到的相应的反作用力.而当粒子受到固体反作用力时粒子速度的计算对交互效果起着重要作用.

计算机图形学中，为了获得粒子与固体碰撞后的速度，一般会通过标准矢量反射方法将流体粒子的速度ui反射到表面法线上[14]：

ui′=ui-2(ui·n)n

(18)

式(18)是一个动能守恒方程，这将产生一个完全弹性碰撞.但流固交互在碰撞处理过程中属于非弹性碰撞，因此引入恢复系数控制碰撞后所剩的动能：

ui′=ui-(1+cR)(ui·n)n

(19)

4 实验结果与分析

本实验基于windows操作系统，在Unity3D平台下建立了流体与固体障碍物的交互模型.硬件环境为：Intel(R) Core(TM) i7 CPU 4790 @ 3.60GHz，8G RAM，显卡为ATI AMD Radeon R7 200 Series.

为了模拟真实气态流体运动时的不规则性，引入柏林噪声，图2为有无添加柏林噪声的未渲染时的烟雾对比图.

图2 烟雾粒子运动对比图Fig.2 Comparisons of the smoke particle motion

图2中，左图为常规SPH方法生成的粒子烟雾效果图；右图为添加噪声之后烟雾运动.由图可以看出，添加噪声后，由于烟雾粒子的运动速度和生命周期是一个随机数值，所以烟雾粒子运动更具不规则性，因此烟雾模型运动细节更加丰富，更加层次分明.

图3 蒸汽模拟Fig.3 Steam simulation

在模拟气态流体方面，除了烟雾，本方法也适用于模拟水蒸汽.图3为本实验水蒸汽和文献实验效果对比图.其中图3(a)为文献[7]中蒸汽效果图；图3(b)为文献[9]中蒸汽效果图，图3(c)为本文方法模拟的蒸汽效果.

通过对比，由于随机数值的粒子速度和生命周期的影响，使得本实验效果较文献中的实验效果在细节上显得更加丰富，更具层次感.

生活中，流体每时每刻都在与不同障碍物发生相互作用.为了模拟真实的交互效果，对固体障碍物添加边界限制，施加反作用力区域.进行了不同形态的流体与不同障碍物交互实验.烟雾与不同障碍物交互的实验效果及与文献对比如图4所示.其中图4(a)为文献[6]烟雾与障碍物交互效果图；图4(b)为本实验烟雾与分别与球体、立方体、中空圆台状固体和绳结状固体交互实验图.

图4 烟雾与不同障碍物交互Fig.4 Interaction of the smoke with different obstacles

由实验图可以看出，文献[6]中的烟雾缺少详细的运动细节，且只能与规则边界的障碍物相互作用；由于本实验对传统的SPH方法及碰撞处理进行了改进，所以烟雾不仅能与简单或复杂边界的固体障碍物自由交互，且具有真实感.

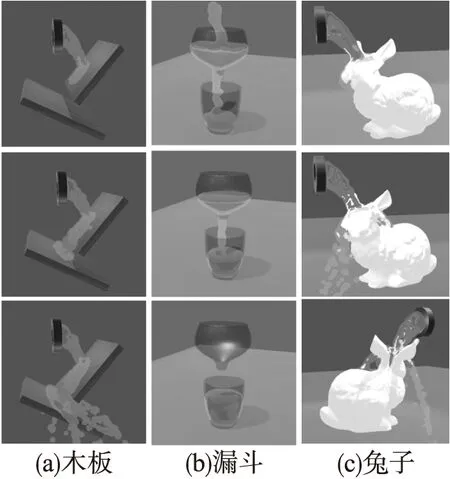
图5 水与不同障碍物交互效果图Fig.5 Interaction of the water with different obstacles

模拟水与不同障碍物交互的实验效果如图5所示.其中，图5(a)为水顺着两块倾斜木板流动的实验效果；图5(b)为水从漏斗顺流到水杯的效果图；图5(c)为将水浇向兔子头上的效果图.

通过实验效果可见，由于固体边界限制力的作用，有效降低了粒子穿透固体边界的可能性，使得流体能与不同固体障碍物自由交互，且具有较真实的流固交互效果.

在容器内添加固体障碍物，模拟流体与有无添加边界限制的固体障碍物交互情况，效果如图6所示.

图6 有无边界限制的流固交互对比Fig.6 Comparison of fluid-solid interactions with or without boundary constraints

图6(a)为容器内的木板没有添加边界反作用力限制，此时流体与木板无相互作用，直接穿透木板；图6(b)为添加边界限制模型的木板，此时木板与流体发生相互作用.

为了模拟更符合真实情况的流固交互效果，引入恢复系数控制粒子与固体碰撞时的动能恢复，不同恢复系数的效果如图7.

图7 不同恢复系数对比实验Fig.7 Comparison of different recovery factors

图7(a)的恢复系数为0.1，接近非弹性碰撞，效果较为接近真实情况；图7(b)中恢复系数为0.5，此时流体粒子与障碍物碰撞时会发生轻微反弹；图7(c)中恢复系数为0.8，此时粒子碰撞时反弹效果明显.

通过多组实验表明，本方法能够实现流固间的自由交互，有效防止了粒子穿透固体边界的可能性，且不再局限为与规则边界物体的相互作用，交互更具多样性，拓展了流体交互领域的应用范围.

流固交互模拟的速度与流体粒子数和障碍物模型的网格复杂度相关，网格模型的复杂程度由网格顶点数和面数量决定，表1给出了不同实验条件下流固交互时的平均帧率.

表1 不同实验条件下的帧率对比
Table 1 Frame rate comparison under different experimental conditions

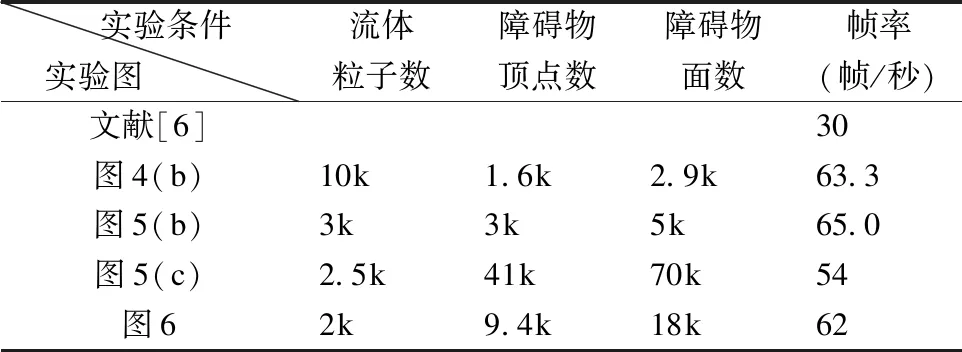
实验条件实验图 流体粒子数障碍物顶点数障碍物面数帧率(帧/秒)文献[6]30图4(b)10k1.6k2.9k63.3图5(b)3k3k5k65.0图5(c)2.5k41k70k54图62k9.4k18k62

由表1可以看出，本实验方法模拟流固交互能很好地满足实时性要求.

5 结 论

在传统SPH方法流体模拟中引入柏林噪声函数求解流体系数，模拟出更具层次感的气态流体运动.考虑到模拟效率的问题，采用计算量较小的蛙跳时间积分方法，并通过边界限制，在模拟出流体与不同障碍物交互的同时减少粒子穿透现象.进一步分析流体粒子与固体障碍物边界发生碰撞时的动能与速度，引入恢复系数控制动能的剩余量，求解出更加符合实际的碰撞效果.通过实验证明，不仅能模拟更具层次感、真实感的流体，同时能很好地模拟流体与不同边界的动态、静态固体障碍物真实交互效果，并且具有良好的实时性.在今后的工作中，将会在弹性物体边界处理方面进一步研究，以期完成流体与弹性物体自由交互，并且将在流体渲染方面进行更深层次的探索，提高流体的真实感