三维本体关联模型下的在线学习路径优化方法

李浩君,聂新邦,杨 琳,张鹏威

(浙江工业大学 教育科学与技术学院,杭州 310023)

1 引 言

随着信息技术与教育应用深度融合发展,在线学习环境出现海量学习资源.然而对于学习者来说如何选择恰当的学习资源以组成适合的学习路径非常困难,此外过多的学习资源会增加学习者认知负荷,影响在线学习效果.当前多数在线学习系统仅依据学习者与学习资源的关联特征进行学习路径优化,并没有考虑知识点的内在关联[1,2].因此在线学习路径优化问题仍是国内外自适应个性化学习研究的热点.

学习路径推荐本质上是一个个性化的推荐问题,通常包含模型建立与优化计算两个方面[3,4].在模型建立方面,使用本体构建模型可以明确知识属性及知识间的关联,提高特征匹配的精确度[5].Lv等人[6]基于领域关联本体设计了推荐系统框架并利用遗传算法进行求解,取得了较好的推荐结果;Tarus等人[7]提出一种基于知识的混合推荐系统,利用本体技术和序列模式挖掘算法给学习者推荐在线学习资源,实验结果表明此方法推荐效果较好,并在一定程度上解决了冷启动和数据稀疏问题;吕刚等人[8]提出基于用户标注信息的本体学习方法,通过设计本体学习模型来帮助用户组织及管理资源,提高标签系统推荐效果.在优化计算领域,应用于在线学习路径的优化算法有多种,粒子群算法因具有参数少、易于理解等优点被不断进行研究探索.Demarcos等人[9]构建了基于能力的学习对象排序问题模型,以能力为基础确定学习单元顺序,并运用粒子群算法进行求解,实现了较好的优化效果;Chu等人[10]提出一种个性化电子课程组合方法,利用粒子群算法将学习资源组合成符合学习者需求的个性化在线课程,提高个性化课程生成效率;吴雷等人[11]提出一种改进粒子群算法求解在线学习路径优化问题,通过采用局部领域搜索与禁忌搜索相结合的方式来提高算法性能,实验结果验证了此方法的实用性和精准性.

当前粒子群算法应用于学习路径优化领域还存在以下不足:1)在线学习路径优化常以学习者和学习资源为核心建立优化模型,忽略了课程信息与学习者、学习资源的关联,优化模型信息片面;2)目前学习路径优化构建的最优问题约束条件较多,影响学习路径推荐的效率;3)二进制粒子群算法易陷入局部最优,学习路径的寻优性能受到限制.

针对以上不足,本文从以下三个方面对学习路径优化方法进行改进:首先利用本体技术构建三维本体关联模型,实现课程信息、学习者信息及资源信息的共享与连接;其次简化学习路径求解过程,将复杂的路径最优问题转化为最短路径求解问题,并利用收敛性较好的二进制粒子群算法进行求解;最后依据算法种群多样性对二进制粒子群算法的映射函数进行调整,使粒子运动更符合规律,提高学习路径优化的效率与精确性.

本文利用本体技术将课程、学习者及学习资源信息相连接构建三维本体关联模型(TDOCM),实现三者信息的共享与关联.大量研究表明,学习资源难度、媒介类型、内容类型与学习者能力、学习风格、认知水平的匹配程度是个性化推荐的关键依据[1,7],因此从这三个方面可以对学习资源进行评价,以判断其是否符合学习者个性化需求.以TDOCM模型为核心并融入种群多样性与映射函数协同更新的二进制粒子群算法(CUBPSO),提出一种三维本体关联模型下的在线学习路径优化方法(TDOCM-LPOM),利用该方法对学习路径进行优化.

2 问题描述和模型建立

2.1 问题描述

学习路径优化本质是依据待学习知识点的学习顺序,将无序的学习资源重组为符合学习者个性化学习的资源序列.在线学习路径优化问题可以描述为:已知课程、学习者以及学习资源的特征信息,在关联本体构建完成的基础上,依据资源背离程度为知识点匹配最佳资源,学习者从当前所学知识点出发按知识点前后序顺序学习其对应的最佳资源,每个知识点对应单个资源全部完成后,结束学习.学习路径优化求解的最终结果为一系列学习资源组成的有序序列,每个知识点有且只有一个学习资源与之对应,优化路径应保证资源学习顺序符合知识点结构关系,所学资源最符合学习者个性化需求且与知识点关联度最大.

2.2 背离度定义

背离度是衡量学习路径优化效果的评价指标,可以检验学习路径中资源信息特征与学习者特征、知识点关联的符合程度.背离度小表明优化效果较佳,学习路径在符合学习者个性化需求的同时,还能保证资源学习顺序符合知识点前后序关系且与知识点关联度最大;反之表明学习路径优化效果较差,不适合开展个性化学习.背离度由背离度优化函数计算获得,用RD表示.

2.3 本体设计

在线学习路径优化核心基础是课程信息、学习者信息和学习资源信息的优化组合,利用本体技术设计课程本体、学习者本体和学习资源本体可以更好地表征特征信息,提高特征匹配精准度.

2.3.1 课程本体设计

课程本体描述领域知识结构,主要包括元数据、章节、知识点以及学习资源四方面特征信息,如图1(a)所示.

课程本体中元数据主要包含课程标题、关键字等描述信息;章节主要包含章节名称、章节结构关系等信息,与知识点构成一对多的映射关系;知识点主要包含知识点名称、知识点结构关系等信息,与学习资源构成一对多的映射关系;学习资源信息主要由学习资源本体进行描述.

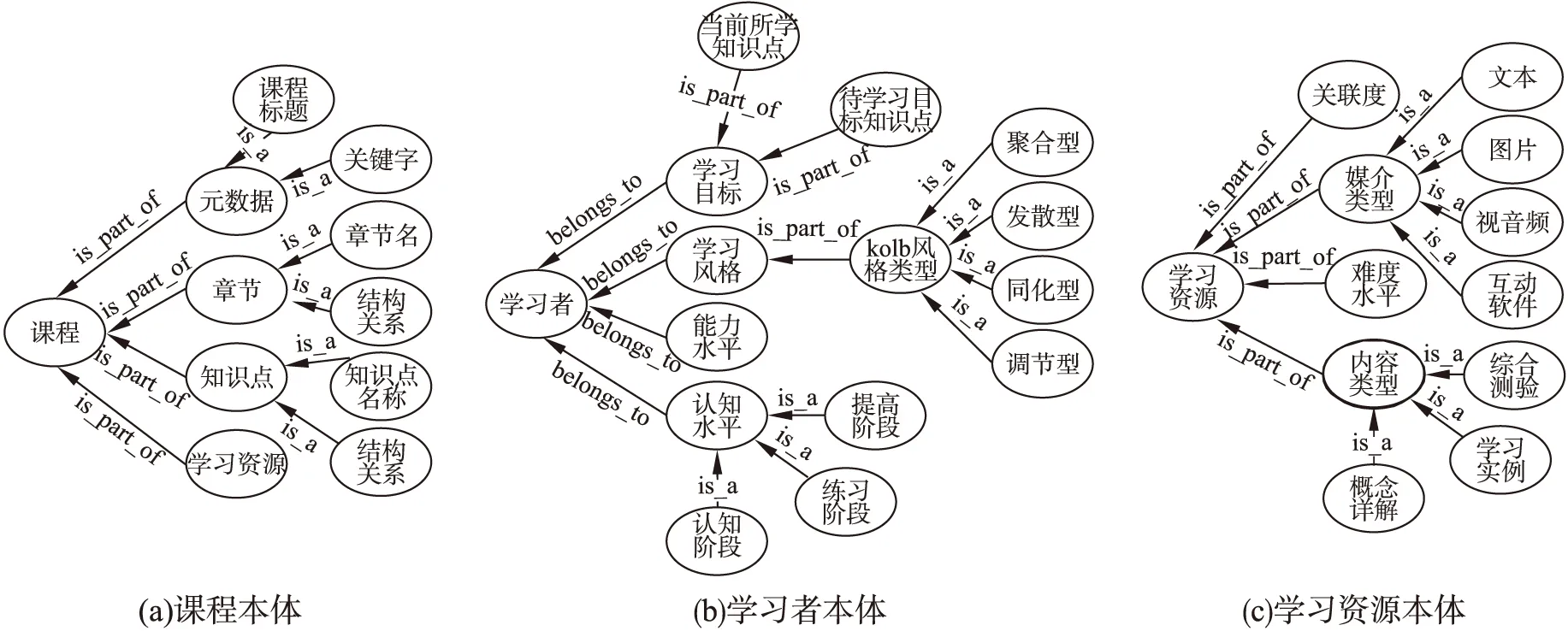
图1 本体设计Fig.1 Ontology design

结构关系有前序关系、后序关系和并列关系三种.若知识点A是知识点B的基础,只有掌握了知识点A才可以学习知识点B,则A是B的前序关系,B是A的后序关系;若知识点C和知识点D属于同一个知识类别,但两个知识点之间不存在前后序关系,知识点学习先后顺序并不影响学习者对知识点掌握效率,则C和D是并列关系.

为提高学习效率,知识点的学习应按前序知识到后序知识的顺序进行,若某一知识点存在多个前序知识点,则该知识点的学习应在前序知识全部掌握后进行.

2.3.2 学习者本体设计

学习者本体描述学习者个性化特征,是学习资源差异评价的依据,主要包括学习目标、学习风格、认知水平以及能力水平四方面特征信息,如图1(b)所示.

学习者本体中学习目标主要包含学习者当前所学知识点以及待学习目标知识点信息;能力水平指学习者的个人能力信息;认知水平指学习者对知识点的认知程度,分为认知阶段、练习阶段及提高阶段三个层次,对应匹配资源的内容类型为概念详解、学习实例及综合测验;学习风格指学习过程中学习者的偏爱方式,包括聚合型、发散型、同化型和调节型四种,对应匹配资源的媒介类型为文本、图片、视音频及互动学习软件.

学习者本体参数定义:

1)定义学习者L={L1,L2,…,Lk}代表K个学习者,K为学习者总数量.

2)定义学习者待学习目标知识点LG={lg1,lg2,…,lgm}代表M个知识点,lgm表示学习者第m个待学知识点,1≤m≤M.

3)定义学习者能力水平A={a1,a2,…,ak}代表K个学习者的能力水平,ak为学习者Lk的能力水平,1≤k≤K.

4)定义学习者的学习风格为e={e1,e2,…,eq}={聚合型,发散型,同化型,调节型},Q表示学习者学习风格数量,Q=4.设LS={ls1,ls2,…,lsk}代表K个学习者的学习风格,其中lsk代表学习者Lk的学习风格,共有Q个一维向量与之对应lsk={lsk1,lsk2,…,lskq},1≤k≤K;lskq的值为实数,表示学习者Lk与第q种学习风格的匹配值,学习者的学习风格并不单一,匹配值大小决定了学习者对q种学习风格的偏好程度,0≤lskq≤1;学习风格匹配值满足约束条件公式(1):

(1)

5)定义学习者对知识点的认知水平KL={kl1,kl2,…,klk}代表K个学习者的认知水平,其中klk代表学习者Lk的认知水平,有m个一维向量与之对应klk={klk1,klk2,…,klkm},1≤k≤K,1≤m≤M,M为待学习知识点的数量,认知水平为认知阶段、练习阶段和提高阶段中的一种.

2.3.3 学习资源本体设计

学习资源与知识点构成多对一的映射关系,学习资源本体描述学习资源特征信息,主要包括难度水平、媒介类型、内容类型以及关联度四方面信息,如图1(c)所示.

学习资源本体中难度水平指学习资源的学习难度;媒介类型指学习资源的媒介类别,包括文本、图片、视音频及互动学习软件;内容类型指学习资源对应的内容类别,包括概念详解、学习实例及综合测验;关联度指学习资源与对应知识点的关联程度,关联度越高则学习资源完成后其对应知识点的掌握越好.

学习资源本体参数定义:

1)定义学习资源R={rm1,rm2,…,rmn},rmn代表第m个知识点对应的第n个资源,1≤m≤M,1≤n≤N,M为待学习知识点数量、N为单个知识点包含学习资源的数量.

2)定义学习资源的难度等级D={d1,d2,…,dm},dm代表第m个知识点的学习资源难度水平,共有n个一维向量与之对应dm={dm1,dm2,…,dmn},dmn为第m个知识点对应第n个学习资源的难度水平信息.

3)定义学习资源的媒介类型为b={b1,b2,…,bq}={文本,图片,视音频,互动学习软件},Q表示学习资源媒介类型数量,Q=4.设MP={mp1,mp2,…,mpm},mpm代表第m个知识点所包含学习资源的媒介类型,共有n个学习资源与之对应mpm={mpm1,mpm2,…,mpmn};每个学习资源包含的媒介类型并不单一,mpmn有Q个一维向量与之对应mpmn={mpmn1,mpmn2,…,mpmnq},mpmnq的值为实数,表示知识点lgm第n个资源与第q种媒介类型的匹配值,匹配值大小决定了某种媒介类型的占有程度,0≤mpmnp≤1;媒介类型匹配值满足约束条件公式(2):

(2)

4)定义知识点对应学习资源的内容类型CP={cp1,cp2,…,cpm},cpm代表第m个知识点对应学习资源的内容类型,共有n个一维向量与之对应cpm={cpm1,cpm2,…,cpmn},cpmn代表第m个知识点对应第n个学习资源的内容类型,内容类型为概念详解、学习实例和综合测验中的一种.

5)定义学习资源与知识点的关联度CL={CLm1,CLm2,…,CLmn},CLmn代表知识点lgm与其第n个资源的关联度,M为待学习知识点数量、N为单个知识点包含学习资源的数量.

2.3.4 控制变量

定义学习资源推荐路径变量为xij,若学习路径推荐顺序为第i个学习资源到第j个学习资源,则xij=1;否则xij=0.

定义序列变量Sij表示推荐学习资源之间的序列关系,若路径推荐的学习资源i是j的前序关系,则Sij=1;若路径推荐的学习资源i是j的后序关系,则Sij=3;否则Sij=2.

2.4 模型建立

根据本体参数信息,构建在线学习路径三维本体关联模型(TDOCM),如图2所示.

图2 在线学习路径三维本体关联模型Fig.2 Three-dimensional ontology correlation model of online learning path

TDOCM关联模型中,学习者本体与课程本体存在待学习知识点与知识点结构关系的关联映射,课程本体与学习资源本体存在知识点与学习资源的一对多关联映射,通过三维本体关联模型可以实现三者信息的共享与连接.依据本体模型不仅可以对学习者待学习目标知识点进行结构关系标注,使其形成一组符合学习顺序的知识点序列,还可以对学习者与学习资源进行特征差异评价,以差异评分来判断学习资源是否符合学习者的个性化需求.依据知识点与资源的映射关系可以将资源差异评分与待学习知识点序列相关联,构建学习者知识网络.知识网络是学习路径优化函数构建的前提.

2.4.1 知识网络构建

知识网络是一个以知识点为节点,以结构关系和资源差异评分为边构成的知识点偏序拓扑网络,包含学习者待学习知识点、知识点结构关系以及学习资源评分等信息.知识网络的构建由结构关系标注、学习资源评价以及知识网络建立三部分组成.

1)结构关系标注

学习者本体包含学习者待学习知识点,课程本体包含知识点之间的结构关系,通过三维本体关联可以将结构关系映射于对应知识点,形成一组具有结构关系的知识点序列.具体来说,从学习者当前所学知识点出发,依据知识点结构关系标注其后序及并列知识点,直到知识点关系全部标注完毕.

以图3为例,假设学习者共有4个待学习知识点:K1、K2、K3、K4,此时知识点结构关系未知,如图3(a)所示;通过课程本体可知K1是K2、K4的前序知识、K3是K2、K4的后续知识,K2、K4为并列关系,此时结构关系标注后的待学习知识点如图3(b)所示.

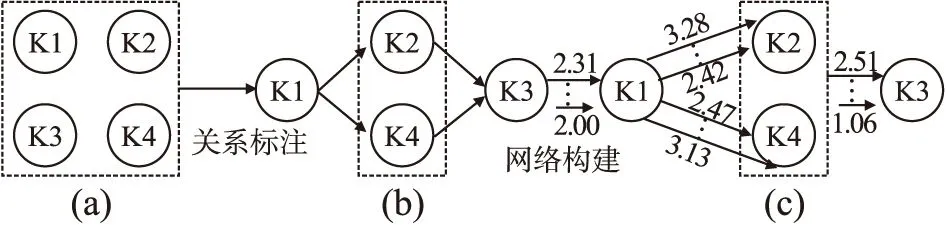
图3 知识网络构建Fig.3 Knowledge network construction

2)学习资源评价

具有前后序关系的知识点可以通过学习资源进行连接,学习者完成对应学习资源即可从前序知识点过渡到后序知识点.知识点间连接的学习资源并不单一,不同学习资源过渡的难度也会存在差异,因此对学习资源进行评价有利于推荐最为符合的资源,提高学习者的学习效率.

学习资源特征参数与学习者特征参数在2.3节已有详细阐述,构建差异评价函数可以对学习资源进行评价,具体如公式(3)所示:

1≤m≤M,1≤n≤N,1≤k≤K.

(3)

DS为学习资源的评价函数,主要由学习者学习风格与学习资源媒介类型匹配函数、学习者认知水平与学习资源内容类型匹配函数以及学习者能力水平与学习资源难度水平匹配函数三部分构成,评价函数中各变量的值为具体实数.DS包含K个学习者对应的学习资源差异评分矩阵,评分矩阵有M*N个向量与之对应.差异评分值可以反映学习资源特征与学习者特征匹配程度,差异评分值小表明学习资源更符合学习者需求,利于个性化学习;差异评分值大表明不利于个性化学习.

依据图3所提知识点及公式(3)评价函数,以单个知识点对应4个学习资源为例进行学习资源评价实验.实验中设置4个知识点、16个学习资源,每个知识点对应的资源分别记为1号、2号、3号及4号学习资源,学习者及学习资源信息由MATLAB按本体参数定义仿真产生.由公式(3)经30次独立运行实验,可以得到各学习资源的差异评分值,如表1所示,最小值加粗表示.

表1 学习资源评价值
Table 1 Learning resource evaluation value

1号2号3号4号K12.313.283.252.00K23.281.431.342.42K32.512.163.191.06K42.471.451.003.13

从表1中可以看出,知识点K1对应的4号学习资源差异评分最低,表明4号资源更符合学习者的个性化需求,可以帮助学习者更高效地掌握知识点K1.同理知识点K2、K3、K4对应的最佳学习资源分别为3号、4号及3号.

3)知识网络建立

知识点与学习资源存在一对多的映射关系,依据学习者待学习知识点序列(图3(b))及其对应学习资源的评价信息(表1)构建知识网络,具体如图3(c)所示.

知识网络中知识点间的联接边由其结构关系和对应资源生成,后序知识点包含的某一资源学习完成后即可从前序知识点过渡到后序知识点.联接边的长度与后序资源的差异评分值成正比,差异评分值越大联接边越长,过渡难度越大.

2.4.2 在线学习路径背离度函数建立

依据学习者知识网络可以将最优学习路径问题分解为三个子问题:学习资源特征与学习者特征最优匹配问题;资源学习顺序与知识点结构关系相符问题;学习资源与知识点关联度最高问题.在线学习路径背离度函数由以上三个子问题函数组合建立.

知识网络中联接边的长度由资源差异评分决定,任意节点间的最短路径可作为选择最优匹配资源的依据,据此第一个子问题可转化为最短路径计算问题;同时学习资源学习顺序与待学习知识点序列关系对应,通过序列变量可以进行控制.构建特征结构函数F(1)可解决前两个子问题,具体如公式(4)所示:

(4)

xij为学习资源推荐路径变量,Sij为学习资源序列变量,DSmn表示某一学习者第m个待学知识点对应第n个学习资源的评分.

为了保证所选学习资源同目标知识点的关联程度最大,构建相关度差距函数F(2),如公式(5)所示:

(5)

Zn表示学习资源的选择情况,值设为1,即考虑在学习资源推荐完成之后的情况下排序;CLmn表示第m个知识点与第n个学习资源的关联度.

为了保证学习过程中每个知识点有且只有一个学习资源与之对应,构建对应约束函数:

(6)

在线学习路径背离度函数RD可由子函数通过加权系数构建,具体公式如公式(7)所示:

(7)

3 模型求解

本文所提出的基于TDOCM模型在线学习路径求解问题与NP难问题较为类似,运用粒子群算法可以有效解决此类问题[12].为了提高在线学习路径优化的效果,在TDOCM模型的基础上设计种群多样性与映射函数协同更新的二进制粒子群算法CUBPSO,提出TDOCM-LPOM在线学习路径优化方法.首先依据种群多样性定义变化因子,其次利用变化因子调整映射函数,使映射函数曲线斜率更符合粒子运动规律,最后运用改进映射函数更新粒子位置与速度,提高算法求解在线学习路径的能力.

3.1 算法设计

通过对原始BPSO[13]映射函数进行改进提出CUBPSO算法.改进算法依据种群多样性的状态调整映射函数,使算法具有较快收敛能力的同时不易陷入局部最优.

3.1.1 定义变化因子

种群多样性可以描述群体中个体的差异性,参照文献[14]本文选用种群多样性计算如公式(8)和公式(9)所示:

(8)

(9)

变化因子cf是调整映射函数的参数,如公式(10)所示:

(10)

div和divmax分别表示当前种群多样性和最大种群多样性的值.

3.1.2 映射函数改进

基本PSO算法适合于求解连续优化问题,而现实世界存在大量的离散型问题,通过映射函数可以将PSO算法转换成二进制版本;S型映射函数是一个Sigmoid函数,属于众多映射函数中的一种.在BPSO算法中,采用S型映射函数将粒子速度值转换成位置向量取1的概率,取值范围为[0,1]之间,依据映射概率值粒子位置向量被强制转换为0或1,S型映射函数如公式(11)所示:

T(vij)=1/(1+exp(-vij))

(11)

vij为粒子速度值,T(vij)表示粒子位置取1的概率.

文献[15]采用固定的控制参数来调整映射函数,映射函数曲线只能线性变化,无法依据算法进化状态实时自适应性调整.文献[16]指出粒子越靠近最优点速度越接近0,当算法处于收敛状态时若粒子速度越快趋于0,则算法更易收敛于全局最优.基于以上分析提出CUBPSO算法,通过变化因子cf调整映射函数以提高算法的性能,改进映射函数公式及其曲线如公式(12)、图4所示.

(12)

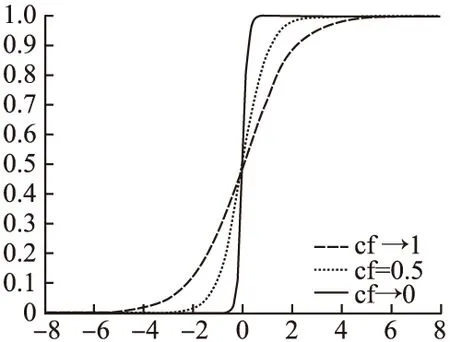
图4 映射函数曲线图Fig.4 Mapping function graph

公式(12)为改进映射函数公式,T(vij,cf)为速度映射概率值,cf为变化因子.由图4可知,映射函数曲线随cf的变化而发生改变,迭代前期算法处于收敛阶段,此时粒子种群多样性较大、cf值较小,映射函数曲线斜率增大、速度映射取0或1的概率增加,算法随机性增强利于全局搜索,同时速度映射概率值的变化可以使粒子速度更快趋于0,算法加快收敛;迭代后期算法处于跳出局部最优阶段,此时粒子种群多样性较小、cf值较大,映射函数曲线斜率变小、速度映射取0或1的概率减小,算法随机性减弱、局部开发能力增强,不易陷入局部最优.

3.2 利用算法优化学习路径求解函数

3.2.1 变化因子计算

利用公式(8)和公式(9)计算当前种群多样性性,利用公式(10)计算本次迭代过程中变化因子的值.

3.2.2 粒子速度更新

CUBPSO采用基本二进制粒子群算法中的速度更新公式.如公式(13)所示:

(13)

ω为惯性权重;c1、c2为学习因子;r1、r2是[0,1]之间的随机数.pij为粒子个体历史最优;gij为种群最优.

3.2.3 映射函数更新

通过公式(12)更新映射函数.

3.2.4 粒子位置更新

粒子位置更新根据速度映射的概率值是否大于随机函数rand来决定,当速度映射的概率值大于随机数rand时粒子位置向量取1,否则取0.如公式(14)所示:

(14)

3.2.5 背离度RD求解

利用改进算法对背离度函数RD进行求解,依据求解结果判断学习路径优化效果.

3.2.6 在线学习路径优化方法TDOCM-LPOM

TDOCM-LPOM学习路径优化方法从模型完善和算法优化相结合的角度来优化在线学习路径.一方面三维本体关联模型融合了学习者本体、课程本体和学习资源本体,在学习者、课程以及学习资源联系更加明确、多样化的基础上构建学习路径背离度函数;另一方面CUBPSO通过进化因子实时调整映射函数曲线,使算法能够快速收敛的同时不易陷入局部最优;最后利用CUBPSO对学习路径背离度函数进行求解,实现最优学习路径推荐.

4 仿真实验

4.1 实验设计

为评判在线学习路径优化方法的计算性能,设计如下四组实验,实验参数如表2所示.

表2 学习路径优化问题模型参数
Table 2 Learning path optimization problem model parameters set

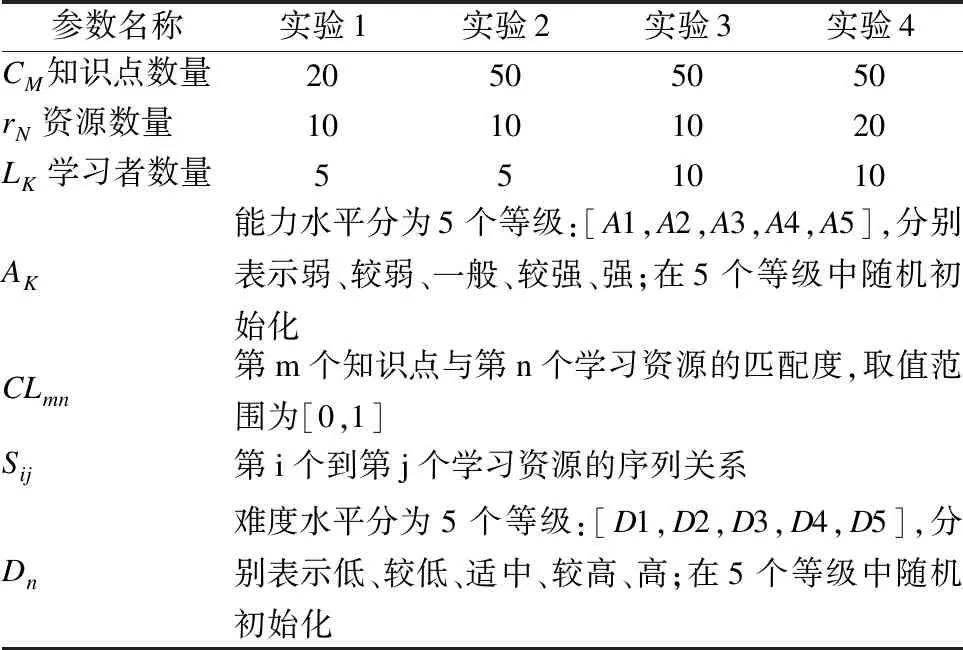
参数名称实验1实验2实验3实验4CM知识点数量20505050rN资源数量10101020LK学习者数量551010AK能力水平分为5个等级:[A1,A2,A3,A4,A5],分别表示弱、较弱、一般、较强、强;在5个等级中随机初始化CLmn第m个知识点与第n个学习资源的匹配度,取值范围为[0,1]Sij第i个到第j个学习资源的序列关系Dn难度水平分为5个等级:[D1,D2,D3,D4,D5],分别表示低、较低、适中、较高、高;在5个等级中随机初始化

问题参数模型中资源数量rN指单个知识点包含的资源量,学习资源总数为CM、rN与LK的乘积;学习者能力水平AK={A1,A2,A3,A4,A5}={弱,较弱,一般,较强,强}分为五个层级,层次越强则能力越强;学习资源难度水平Dn={D1,D2,D3,D4,D5}={低,较低,适中,较高,高}可分为五个层级,层次越高资源学习难度越大.在线学习路径优化过程中,知识点数量、资源数量以及学习者数量不同其路径优化的效率和精准度也有所偏差,为此本文设置不同数量的学习者、知识点及学习资源进行对比分析,以观察学习路径优化性能.实验1、实验2对比不同知识点数量对实验效果的影响,实验2、实验3对比不同学习者数量对实验效果的影响,实验3、实验4对比不同资源数量对实验效果的影响.

在实验设计完成的基础上,以TDOCM模型为核心分别融合BPSO[13]、IPSO[17]、TVT_BPSO[15]及CUBPSO算法进行实验,分析实验效果验证本文所提在线学习路径优化方法的执行效率与精准度.文献[13]提出二进制粒子群优化算法(BPSO)以解决离散性问题,本文其他对比算法都以BPSO为基础;文献[17]所提问题解决模型与TDOCM模型的构建思想相似;文献[15]针对映射函数改进算法,与CUBPSO的改进角度类似;因此选用以上算法进行对比实验.

实验中各算法均采用S型映射函数,其中BPSO为基本二进制粒子群算法,IPSO采用惯性权重线性递减策略改进算法,TVT_BPSO及CUBPSO的改进策略类似但有所差异,前者通过控制变量线性调整映射函数,后者依据种群进化状态自适应调整映射函数.算法具体参数设置如下:种群规模N=20,学习因子c1=c2=2,最大迭代次数Max_iteration=100;BPSO、IPSO惯性权重ω取值范围为[0.4-0.9],TVT_BPSO、CUBPSO惯性权重值为1;BPSO、IPSO最大速度Vmax=6,TVT_BPSO、CUBPSO最大速度为Vmax=8.

4.2 实验环境

算法仿真实验环境为windows7操作系统,编程语言环境为Matlab R2012a.硬件环境为intel酷睿处理器i5-4570,主频为3.20GHz,内存为4GB.

4.3 实验结果分析

4.3.1 寻优精度对比分析

寻优精度通过均值和方差进行分析,算法实验数据均在实验平台上独立运行30次获得,最优值用加粗表示,如表3所示.

表3 实验仿真结果
Table 3 Experimental simulation results

核心算法实验1实验2实验3实验4BPSOavg1.45E+035.68E+031.37E+046.80E+04var3.22E+045.53E+052.54E+064.32E+07IPSOavg2.08E+036.91E+031.54E+047.37E+04var4.71E+047.86E+052.80E+065.13E+07TVT_BPSOavg1.22E+034.76E+031.14E+045.47E+04var2.76E+045.18E+051.65E+063.23E+07CUBPSOavg4.17E+021.97E+034.95E+032.32E+04var3.60E+039.23E+042.77E+057.03E+06

背离度函数的构建可以检验学习路径中资源信息特征与学习者特征、课程信息特征的符合程度,背离度小表明优化效果较佳,学习路径在符合学习者个性化需求的同时,还能保证资源学习顺序符合知识点前后序关系且与知识点关联度最大.表3数据为各算法对学习路径背离度函数求解结果的均值和方差,从整体来看,在不同知识点数量、学习资源数量及学习者数量的情况下,本文提出的CUBPSO算法所得均值及方差最小,表明该算法规划的学习路径更加稳定且精准性更高;从对比试验的求解数据变化来看,同一试验组中CUBPSO两次数据差异最小,表明该算法在不同状态下仍具有较好优化性能、算法适应性强;因此运用CUBPSO核心算法构建的在线学习路径优化方法具有更好性能.

4.3.2 寻优过程对比分析

图5为四种算法构建的在线学习路径背离度函数收敛曲线,从图中我们可以更加直观对比各算法的寻优过程.基于实验参数变化来看,对比图5(a)和图5(b)可以看出不同知识点数量下CUBPSO算法呈现出较好的优化速度和优化效果;对比图5(b)和图5(c)可以看出随着学习者数量的增加CUBPSO性能依然稳定,能够在满足学习者个性化需求的同时保持较好的优化速度;对比图5(c)和图5(d)可以看出随着路径优化复杂度的增加BPSO、IPSO及TVT_BPSO算法易出现过早收敛、陷入局部最优等问题,CUBPSO仍保持较好的优化效果.基于实验迭代次数变化来看,迭代前期CUBPSO算法收敛速度快于其他算法,这是由于CUBPSO算法中映射函数曲线斜率的增大加快了算法的收敛速度;迭代后期各算法都表现出一定的寻优能力,而CUBPSO算法此时函数曲线斜率变小、局部开发能力增强,寻优精度最佳.因此随着学习资源总量和迭代次数的增加,CUBPSO的稳定性和精准性更好.

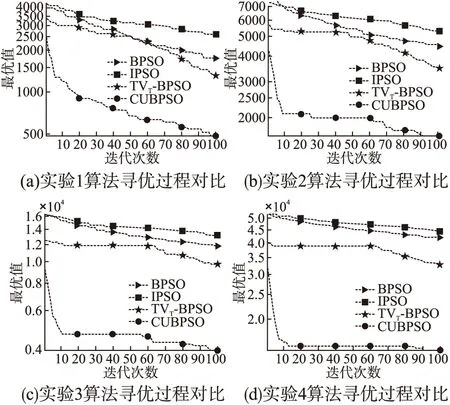
图5 寻优收敛曲线Fig.5 Optimization convergence curve

4.3.3 寻优时间对比分析

为分析各算法构建在线学习路径优化方法的时间花费,参照上述参数设置独立运行各算法15次,依据运行时间平均值绘制时间曲线,如图6所示.

图6 各算法在线学习路径寻优时间Fig.6 Online learning path optimization time of each algorithm

从图中可以看出资源总量小时曲线相对集中,各算法寻优时间相差不大;随着资源总量的增加寻优时间差距越来越明显,BPSO算法运行时间最短,TVT_BPSO、IPSO次之,本文所提出的CUBPSO寻优时间较长,表明当学习资源总量较大时改进算法的寻优效率受到一定限制.

5 结论和未来工作

本文针对目前在线学习路径优化方法存在问题,提出一种三维本体关联模型下的在线学习路径优化方法TDOCM-LPOM.通过定义课程本体、学习者本体及学习资源本体,构建三维本体关联模型,将学习路径最优问题转化为最短路径求解问题,并利用改进的CUBPSO算法对背离度函数进行寻优;实验结果表明,TDOCM-LPOM方法具有更好的稳定性与精准性,所优化的学习路径更符合学习者的个性化需求.后续将对影响个性化学习的主观因素进行细致分析,建立更加完善的在线学习路径优化模型,同时将借鉴人工智能技术进一步提高优化效果.