考虑遮挡情况的光流场估计算法

王 松，汪增福

(中国科学院 合肥智能机械研究所，合肥 230031)(中国科学技术大学 自动化系，合肥 230026)

1 引 言

光流场估计在计算机视觉领域具有重要的地位，它在物体跟踪[1]、图像配准[2]以及运动检测[3]等方面具有广泛的应用.按所使用方法的原理进行划分，最常见的两种算法是微分法和匹配法[4].

微分法是基于颜色一致性和全局平滑性等假设，通过构建合适的能量函数来实现光流场估计的算法.直接使用微分法的缺陷是其不能处理大位移的光流场估计问题.为此，Lucas和Kanade于1981年提出了一种经典的由粗到精的形变补偿光流场估计框架(coarse-to-fine warping scheme)[5],开启了光流场估计研究的热潮.其后三十多年间涌现了大批相关的研究工作.例如，Wedel A等人[6]使用ROF模型对输入图像进行结构-纹理分解以抑制或消除阴影、反光等因素对光流场估计的不良影响；Aubert G等人[7]对所使用能量函数的数据项进行了改进，由单纯使用颜色信息，过渡到使用颜色的梯度信息、二阶梯度信息和梯度模信息等，显著提升了所引入数据项的有效性；Monzón N等人[8]则对能量函数的平滑项进行了改进，他们通过在图像边缘处引入非连续性平滑约束以抑制光流计算中的过平滑现象.

匹配法是将光流场估计问题转化为特征匹配问题进行求解，利用特征匹配计算获得光流场的估计.考虑到算法的计算效率和鲁棒性等因素，其通常不会逐点进行匹配计算，取而代之的是或者以小图像块为单位完成匹配计算[9]或者利用下采样技术对低空间分辨率的图像进行匹配计算[10]，由此获得的光流计算结果是相对比较粗糙的，或者精度上有欠缺，或者空间分辨率不够.为了克服上述方法存在的缺陷，有人提出了基于图像邻域信息的匹配传播算法[11,12].这一类方法虽然能在一定程度上提升光流算法的性能，但其结果的好坏严重依赖于对初始光流的计算.近年来，基于深度学习的算法也得到广泛的研究，形成了以下三类光流算法：端到端的算法[13,14]、基于匹配网络的算法[15]、基于多源信息融合的算法[16,17].

上述算法大多通过提升数据项和平滑项的鲁棒性来抑制遮挡的影响.基于数据统计先验，Lorentzian惩罚项[18]、L1惩罚项[19]和Charbonnier惩罚项[20]先后被提出.平滑项有助于扩散光流场，推理遮挡区域的光流，但也会导致光流结果中的过平滑现象.为此，Weickert等人[21]提出的各项异性正则化策略保留了光流场的不连续性.另外，Kennedy等人[22]提出一种基于三角剖分的几何模型，利用区域联合信息进行遮挡推理.Xu等人[23]通过优化一个平方伪布尔函数(QPBO)将遮挡和被遮挡像素进行联合优化.双边滤波[24]，光流散度[25]及双向光流一致性检查[26]等也被用于遮挡判断，此外还有基于三维场景重建及多帧信息等遮挡处理算法[27].

理论上遮挡区域的光流是没有意义的，但在现实应用中对大多数场景又需要有一个稠密的光流结果.光流场估计的一个基本假设是运动前后的特征一致性，而遮挡现象完全破坏了此约束，将原本一一对应的运动关系变成了一对多或一对零的不确定性关系，从而大大增加了光流场估计的难度，进而影响到全局光流估计的质量.因此，将遮挡区域识别出来对于光流场估计问题来说尤为必要.换个角度而言，如果有完备的运动描述，遮挡推理问题亦可迎刃而解.由此可知光流场估计和遮挡推理是高度耦合的，是“鸡生蛋，蛋生鸡”的问题.而上述方法中，有的没有重视遮挡问题，有的忽略了问题的耦合性，有的计算复杂度极高并且有大量的计算冗余.

基于以上分析，我们提出一种高效的遮挡推理和光流场估计迭代优化算法.如图1所示，图像左列由上到下分别是运动前图像、运动后图像和真实光流结果，图像右列为形变补偿图像和真实遮挡结果.放大图像中的“重影”区域，我们发现其和遮挡区域高度重合，在后续章节中我们将证明二者间的一致性.因此我们可以将遮挡推理问题转换为“重影”区域定位问题.我们使用映射矩阵反向推理，颜色信息和邻域信息相融合的策略获得了可信的“重影”区域定位结果.将上述信息用于修正优化函数和形变补偿图像可以优化光流场估计结果.优化后的光流结果通过改变形变补偿图像又能影响遮挡区域的定位结果.综上，我们构建了一个遮挡推理和光流场估计的迭代优化计算框架.同时，我们发现较好的遮挡推理结果能提升光流估计精度，所以我们引入了循环后处理策略以最大限度地利用遮挡信息.本文贡献主要有以下两点.

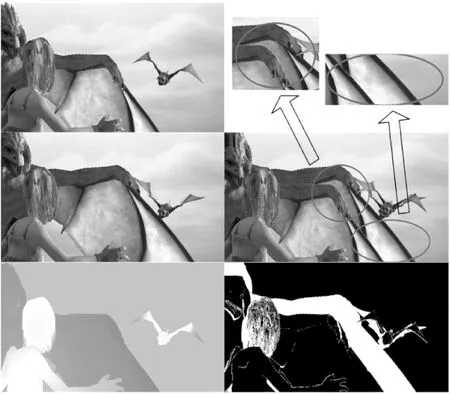
图1 “重影”区域示意图Fig.1 Illustration of the ghosting artifacts

在遮挡推理方面，我们从形变补偿图像中挖掘遮挡信息，通过“重影”区域的识别和定位我们获得了可靠的遮挡推理结果.通过对比形变补偿图像和运动前图像，理想情况下即可获得可靠的“重影”区域定位结果，但是由于光照变化，光流场估计不准确等原因常会出现误判现象.因此我们利用前背景运动统计差异、邻域遮挡一致性等先验知识提高定位的精度及可靠性，最终高效地获得了可靠的遮挡推理结果.

在光流估计方面，我们从问题的本质出发，使用光流估计和遮挡推理的迭代优化框架获得光流估计结果.遮挡推理可用于修正形变补偿图像和优化函数，从而在金字塔的层间传递和层内计算中同时消除了遮挡区域的影响，获得可靠的光流估计结果.光流估计结果在下一次迭代中会通过改变形变补偿函数达到修正遮挡推理的目的.不需要双向光流等复杂的函数构建方法，我们以形变补偿图像为纽带，即可通过迭代优化获得更高精度的光流估计结果.此外，我们还充分利用遮挡推理的优势，使用循环后处理策略优化结果，提升了光流估计精度.

2 基于金字塔结构的光流场估计算法

基于金字塔结构的形变补偿光流场估计框架在深度学习算法[28]和经典算法[29]中都被广泛的使用.此框架的核心是金字塔结构和形变补偿图像，我们将在此分别介绍.

2.1 金字塔结构

经典的光流场估计能量函数由数据项和平滑项构成，如式(1)所示.常用的数据项(式(2))为亮度不变假设，即假设图像序列中对应点的亮度在运动时不发生变化.在后续工作中，为了提升算法鲁棒性，常引入梯度不变假设、海森矩阵不变假设等.平滑项(式(3))的作用为扩散光流场，去除异常点的同时也能推理非遮挡区域光流.函数中x是二维图像中的位置坐标(x,y)，ω是水平和竖直方向上的光流值(u,v)，ω(x)是x位置的光流值，Ψ是Charbonnier惩罚函数，Ω是整个图像域，α是调节系数.

E(ω)=Ecolor(ω)+αEsmooth(ω)

(1)

(2)

(3)

由于式(1)是非线性的，为了计算的便利需要取一阶泰勒多项式近似拟合，且光流值ω越小结果越可靠.在实际场景中，位移量多不能满足苛刻的近似条件，所以常借助金字塔结构来求解光流场问题.先求解低分辨率下的光流场，然后以之作为高分辨率下运动的初始值，经过多次迭代最终获得原图分辨率下的光流场估计结果.

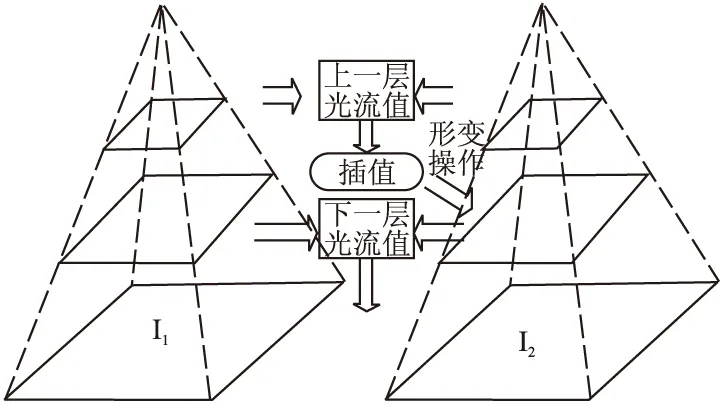
图2 金字塔结构示意图Fig.2 Illustration of the coarse-to-fine spatial pyramidal optical flow estimation scheme

2.2 形变补偿图像

在上述流程中，形变补偿图像既传达了前一层的光流信息，又是当前层的计算对象，在计算过程中占据了举足轻重的地位.由于其通过形变(warp)计算获得，在整体计算框架中有运动补偿的效果，所以命名为形变补偿图像.

光流值为亚像素级，所以从计算代价考虑，多使用后向映射算法，即对第二帧图像进行形变操作.通过某位置的光流值可找到其运动后(即第二帧图像中)的对应位置.若对应坐标非整数，常用邻域信息在第二帧图像中插值获得相应像素值，然后将之作为形变补偿图像中当前位置的像素值.利用光流值可得映射矩阵，即逐点的运动后坐标，利用映射关系和运动后图像即可获得形变补偿图像.

3 遮挡推理和光流场估计算法

由于遮挡推理和光流场估计问题高度耦合，我们提出了一种高效的迭代优化算法.在3.1中将解释“重影”区域和遮挡的关系，在3.2中阐述遮挡推理算法，在3.3中提出优化的光流估计算法，在3.4中提出循环后处理方案.

3.1 “重影”区域和遮挡

我们以图3为例演示“重影”区域的产生.图中第1行的两幅图像分别为三角形区域运动前后的图像，即三角形由图像左侧平移到右侧.第2行中的阴影区域表示不同参考系下的遮挡区域.左侧图像指第二帧图像中缺失的运动前像素，右侧则是第一帧图像中缺失的运动后像素.第3行两幅图像分别是光流结果和形变补偿图像.由于第2帧图像中缺乏背景区域像素信息(如第2行左侧图像所示)，而只能借助前景信息进行错误的填充，从而使得形变补偿图像中出现了“重影”现象.也正是这种场景信息的“缺失”，使得图1中“翅膀”区域出现“重影”现象.

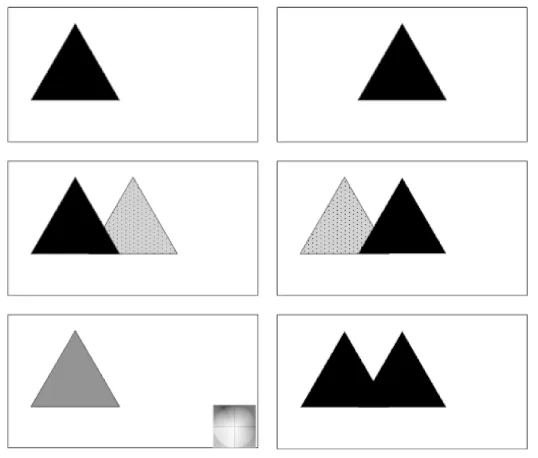
图3 “重影”现象和遮挡关系示意图Fig.3 Toy example of the relation between the ghosting artifacts and the occlusion

这种信息的“缺失”是由运动产生的遮挡引起的，由上分析可知信息“缺失”导致了“重影”现象.因此通过“重影”区域的定位，我们即可获得遮挡推理结果.

3.2 遮挡推理算法

通过光流结果可以获得逐位置的映射关系，若两个像素映射到同一位置，就可判定出现了遮挡现象.定位形变补偿图像中的“重影”区域也可获得遮挡区域标注.利用邻域的运动一致性也推理遮挡.将上述多种策略融合可获得更可靠的遮挡推理结果.

3.2.1 基于映射矩阵的遮挡推理方案

Ilg等人[30]在Flying Chairs[13]和MPI-Sintel[31]等数据集上统计发现前景区域的位移量一般远大于背景区域.在多数场合中，被遮挡区域常出现在背景区域中.因此，如果有多个像素映射到同一位置时，保留光流最大的映射关系，其他则可判定为被遮挡位置.此即为基于运动先验的遮挡推理策略，其计算流程如图4(a)所示.

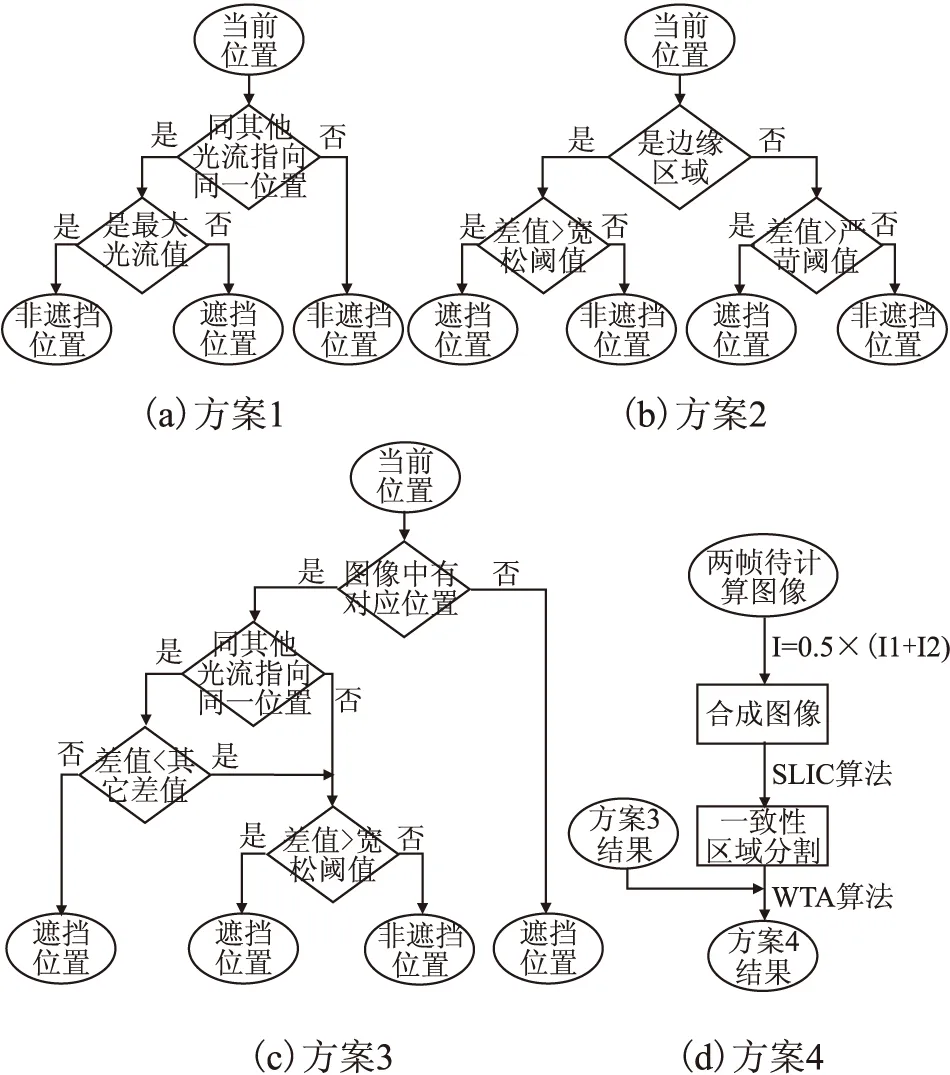
图4 四种遮挡推理方案流程图Fig.4 Flow chart of four occlusion reasoning schemes

3.2.2 基于“重影”区域的遮挡推理方案

由上分析可知，运动后图像依据光流进行逐像素回溯时即可得到形变补偿图像.所以在理想状态下，形变补偿图像和运动前图像应该完全一致，若有任何差异则可判定是由遮挡引起的信息“缺失”导致的.但在实用场景中，光流估计误差、光照变化、插值误差等等均会导致像素变化，所以常设定一个阈值用于对上述差异值进行筛选判断，如果差值过大则标记为遮挡区域.由于形变补偿图像中的像素大多是邻域插值获得，所以我们提出一种基于邻域内像素最大差值的阈值产生策略.图像在边缘区域像素值会变化明显，在平滑区域则没有明显变化.基于以上分析，我们提出对边缘区域和非边缘区域设置不同的阈值以提升算法鲁棒性.其计算流程如图4(b)所示.

3.2.3 融合映射和“重影”的遮挡推理方案

由上分析我们发现方案1是基于一个较强的先验知识，但是合成数据集上的统计结果可能不适用于现实场景中.方案2不需要一个较强的先验但是它对阈值的选取十分敏感.严格的阈值会产生误判，而宽松阈值则会导致漏检现象.

我们尝试将上述两种方案进行融合，利用先验知识进行初步的筛选，然后使用颜色等信息进行精细判断.具体方案如下：先使用映射关系将运动前像素分为三类，1)运动后视场内没有位置的像素与之对应，2)运动后有唯一的位置与之对应，3)和其他运动前像素共同对应到一个运动后位置.第一种情况可直接判定为遮挡.第三种情况下比较所有像素和对应像素的差值，仅当此为差值最小的像素时才会保留对应关系，其他即可直接判定为遮挡位置.一一对应关系时可通过设定阈值进行遮挡判断.此方案能降低对阈值选取的依赖，提高算法的鲁棒性.其计算流程如图4(c)所示.

3.2.4 基于邻域信息的遮挡推理方案

由于运动具有区域一致性，且运动产生遮挡现象，所以遮挡也具有某种程度的区域一致性，则邻域信息可用于遮挡判断.遮挡是由两个物体相向运动产生，所以遮挡区域的边缘既会出现在前一帧图像的边缘上，也会出现在后一帧图像边缘上，所以我们不能单独提取一帧图像中的一致性区域进行遮挡判断.我们首先融合运动前后图像，然后使用SLIC算法获得一致性区域分割结果，最后借助之前遮挡推理结果，使用WTA算法获得区域的遮挡判断结果.本方案充分利用邻域信息，去除了部分异常点，进一步提高了算法精度和鲁棒性.在后续实验中以此作为最终的遮挡推理方案，其计算流程如图4(d)所示.

3.3 光流场估计算法

在基于金字塔结构的计算框架中，我们利用前一帧图像和形变补偿图像计算光流值.前一帧图像中的遮挡区域会破坏一致性假设，若依旧全局优化能量函数则必然会影响整体的计算精度.形变补偿图像中的“重影”区域使得一个像素值至少存在两个对应像素，这在能量函数优化过程中也引入了大量不必要的歧义.因此我们需要借助遮挡推理结果，在光流估计过程中修正上述问题带来的影响.

对于前一帧图像中的遮挡区域，我们使用遮挡系数修正优化函数从而消除遮挡区域对优化过程的影响.将之前遮挡推理结果归一化后作为遮挡系数带入能量函数中，如式(4)所示.其中θ是二值化的遮挡系数，引入此参数即将遮挡区域抠除.α和β为调节参数，引入梯度项约束(式(5))增加算法的鲁棒性.我们选用逐次超松驰迭代法(successive over-relaxation，SOR)去求解此线性等式系统.关于欧拉等式的构建、微分计算和固定点迭代等算法细节我们推荐文献[32].

E(ω)=θEcolor(ω)+αθEgradient(ω)+βθEsmooth(ω)

(4)

(5)

形变补偿图像中的“重影”区域也可以使用遮挡推理定位和抠除.对于空白区域，我们尝试了多种填充策略，包括使用邻域信息平滑等，最终发现通过对应关系利用前一帧图像中对应像素填充能获得最佳的光流估计结果，因为就从计算流程来看，前一帧图像中的相关信息才是正确的像素值.

上述算法不仅将遮挡信息融入能量函数中，直接在每层的光流值计算时去除了遮挡的影响；还利用遮挡信息修正了形变补偿图像，使得在层间的信息传递中也消除了遮挡的影响，借此完整地消除了遮挡现象对目前算法框架的影响.在后续的计算过程中，在新的光流结果指导下可获得更可信的形变补偿图像，从而获得更可靠的遮挡推理结果.我们将两个过程融合在金字塔结构的计算框架下，考虑到算法高效性的同时也保留了二者相互影响的内在关系.

3.4 循环后处理策略

EpicFlow是经典的稀疏光流稠密化算法，与之不同的是，我们提出了一种针对稠密光流的后处理算法.阶段非凸算法(graduated non-convexity algorithm，GNC)指出即使待处理函数是凸函数，此算法也能通过提供一个更好的初始值而优化计算结果，由此启发我们提出循环后处理策略.由于低分辨率下光流场估计的精度不高会影响遮挡推理的准确性，而在高分辨率下能获得更可靠的遮挡推理结果.我们提出将优质的遮挡结果用于低分辨率图像中，发现其对实验结果有明显的提升作用.

我们尝试了多种迭代次数和采样率的参数设置方案.关于迭代次数的选取,我们发现在固定采样率的情况下,若迭代次数越多,即图像下采样次数越多,则初始遮挡信息利用的越少,这背离了本节算法设计的初衷.反之若迭代次数过少时，算法则没有办法充分发挥遮挡信息和光流估计联合处理的优势.关于采样率的选取，多篇文献中给予了不同的建议，如Brox等人[29]采用了稠密采样，采样率设为0.98；Sun等人[33]采用稀疏采样，采样率设为0.5.在固定迭代次数的情况下，若采样率过高，会造成大量的计算冗余，极大的影响了算法的计算效率.反之如果采样率过低，则会在金字塔的层间传递中丢失大量的有用信息.在后续实验中我们发现采样率过低时，光流精度有明显的下滑，而采样率高到某个程度后，其对结果影响不明显.通过上述分析，我们发现迭代次数和采样率均存在一个恰当的取值区间，综合考虑计算效率和计算精度，我们选取迭代次数为3，采样率为0.7.我们在4.3节中展示了参数设置的相关实验细节.

4 实验及结果分析

在两个公开数据集Flying Chairs[13]和MPI-Sintel(包含clean版本和final版本)[31]上评估本文算法的效果.本文以Brox等人[29]提出的LDOF算法作为主要的对比算法.End point error(EPE)是整幅图像的估计光流值和真实光流值的欧式距离，average of EPE(AEE)是算法在整个数据集上的平均性能.

4.1 遮挡推理方案对比

图5是3.2节中提出的四种遮挡推理方案的可视化结果，其中每列的第1行为合成图像，第2行为真实遮挡结果，第3行到第6行分别是由4种方案获取的遮挡推理结果，并标记了IoU量化指标.基于映射矩阵的方案1计算速度最快，但是由于其理论的不完备会使结果出现误检或漏检的现象，比如第3列中的错误就是因为前景区域的光流小于背景区域.基于“重影”区域的方案2取得了可观的结果，但由于对阈值的选取较为敏感，比如第2列的该方案结果就出现了漏检现象，而在第四列中出现了误检.融合两种信息的方案3较于方案2可使用更宽松的阈值设置而不用担心大量的误检现象.基于邻域信息的方案4能很好的抑制异常点从而进一步提高算法的鲁棒性.

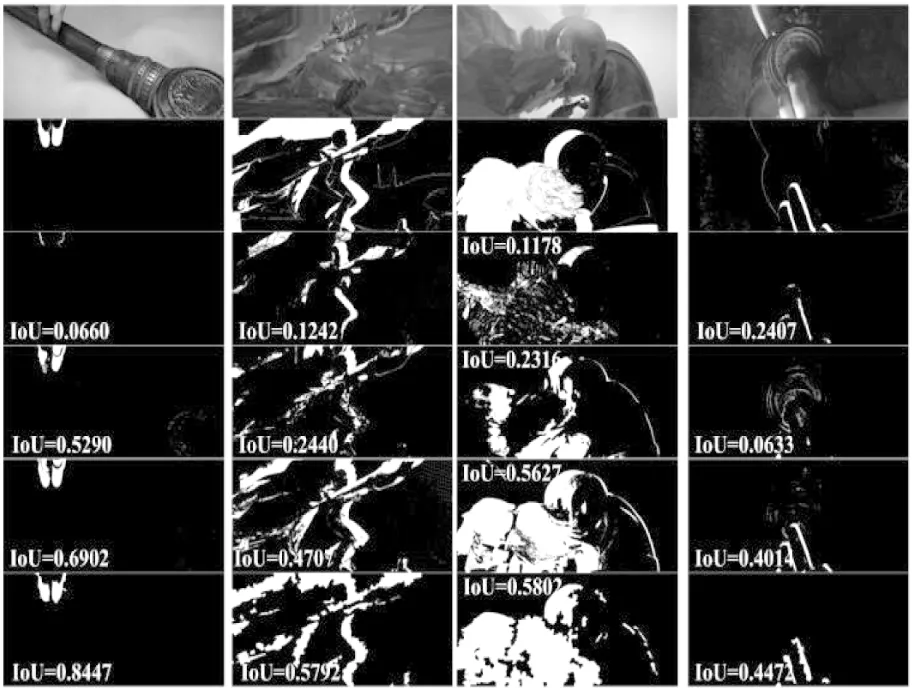
图5 MPI数据集中不同方案下的遮挡推理结果Fig.5 Illustration of occlusion detection results on MPI-Sintel dataset

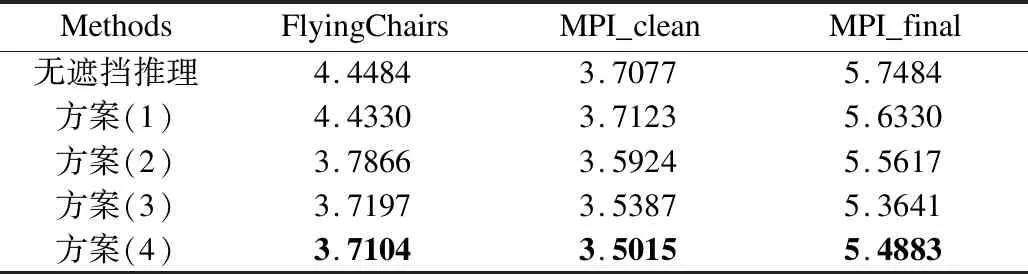
表1 不同数据集下4种遮挡推理方案的光流场估计结果Table 1 Illustration of optical flow estimation of four occlusion reasoning schemes under different datasets

我们在数据集上评估四种遮挡推理方案，并将结果汇总于表1.实验验证了遮挡推理的质量会明显影响光流场估计结果.方案1的遮挡推理算法在光流场求解中没有表现出明显的优势，而其他三种方案均显示出积极的作用.统计结果显示，基于邻域信息的融合方案获得了最佳的光流场估计结果.

4.2 遮挡信息使用方法对比

在3.3节中，我们提出修正能量函数和形变补偿图像两种方案消除遮挡对光流场估计的影响，实验以第三种遮挡方案为例，统计了不同数据集下的光流场估计结果并汇总于表2.M0是原始结果即不进行修正操作，M1是仅修正形变补偿图像，M2是仅修正能量函数，M1+M2是两种方法同时使用.实验验证两种方法同时使用是能获得最佳的光流估计结果，同时实验结果也指出修正能量函数对结果影响更明显，从另一个侧面显示了遮挡对光流估计精度的影响.

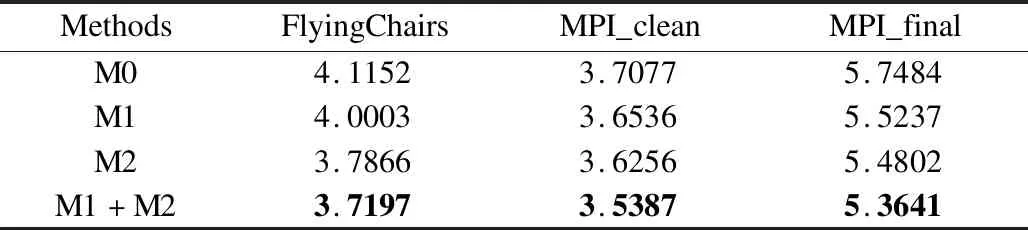
表2 不同遮挡信息使用方法的光流场估计结果Table 2 Average end-point error (AEE) on different occlusion handling strategies

4.3 循环后处理参数

在这一小节中，我们以MPI-Sintel中的clean训练集为例，尝试循环后处理中不同的迭代次数和下采样率对实验结果的影响.

表3 不同迭代次数下的光流场估计结果Table 3 Average end-point error(AEE)on different iterations levels

表4 不同采样率下的光流场估计结果Table 4 Average end-point error(AEE) on different downsampling factors

表3展示的是不同迭代次数对实验结果的影响，此时默认采样率为迭代过程中使用的参数值0.8.我们发现在迭代次数为3时取得结果较好，如果进行更深的迭代，则会因为失去更多光流信息而导致结果变差.表4固定迭代次数为3，考虑不同下采样率对结果的影响.当采样率设置过小时会失去过多的已知光流信息，而设置过大时会有大量的计算冗余.我们也尝试了多次循环后处理，但是发现其对结果的改进并不明显，考虑到算法的效率和鲁棒性，我们将迭代次数设为3，采样率设为0.7.

图6 光流场估计结果示意图Fig.6 Illustration of optical flow estimation on Flying Chairs dataset

4.4 综合实验结果

图6为我们方法和LDOF算法在部分训练数据集上的可视化结果，其中第1列为运动前图像，第2列为运动后图像，第3列为真实光流结果，第4列为LDOF算法获得的光流结果，第五列为我们算法获得的光流结果.图像的右下角为光流值误差指标.在第4行中，LDOF算法几乎没有获得任何有用的运动信息，但是我们方法获得了较好的光流场估计结果.在第1行中，LDOF算法丢失了椅背的轮廓，但是我们方法能很清晰的获得椅背的栅格，这正是得益于对于遮挡区域的正确判断.而在第2行中，LDOF算法的可视化图中几乎看不出是椅子，而我们的算法能精确刻画椅子的扶手和滚轮.在最后一行中，右上角的光流结果验证了我们方法在发生交叠运动时的有效性，较于LDOF算法，我们方法能很好的表现两个椅子不同的运动轮廓，而不是像LDOF算法一样重合在一起.交叠在一起就会产生大量的遮挡，所以这个实例很好的显示出我们算法的有效性.

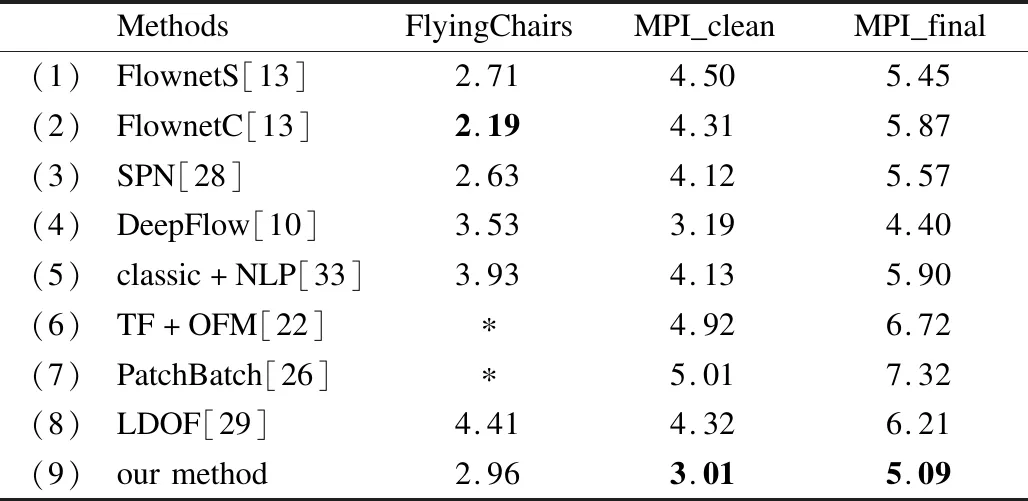
表5 多种算法的光流场估计结果Table 5 Average end-point error(AEE)on different methods

表5汇总了多种算法在当前数据集上的结果.(1)-(3)为基于深度学习的光流场估计算法，(4)和(5)是经典光流场估计算法，(6)和(7)为经典的考虑遮挡问题的光流场估计算法，其文中没有提供在Flying Chairs数据集上的光流结果，(8)为LDOF算法，(9)为本文算法.我们结果远超了LDOF算法.同近些年其他算法乃至和深度学习的算法相比，我们的结果也是富有竞争力的.

5 结 语

本文提出一种高效的遮挡推理和光流场估计迭代优化算法.算法以形变补偿图像为纽带，利用“重影”现象和遮挡区域的内在关系，并结合邻域关系等信息，以迭代优化的形式求解存在遮挡现象的光流场估计问题.我们还提出了循环后处理策略，实验验证了此策略对光流求解问题的有效性.我们的遮挡推理策略从形变补偿图像出发，其也能很好地融入现在愈渐成熟的深度学习框架中，在后续工作中可以考虑将之和深度学习相结合获得更好的结果.