一种障碍物检测移动节点定位算法研究

单志龙,黄 恒,项 婉

1(华南师范大学 计算机学院,广州 510631)2(华南师范大学 网络教育学院,广州 510631)

1 引 言

无线传感器网络[1]所提供的服务经常需要附加一定的位置信息才有其实际效用,例如环境监测[2]中须同时报告异常及其发生的地点,才能使异常得到迅速和准确的处理.目前,虽然GPS定位技术较为成熟,但成本、功耗和非视距影响等因素限制了其在一些场景中的应用,例如在地下室里,GPS信号会受到遮蔽干扰等.针对这些特定的场景,质心定位[3]算法、DV-Hop定位[4]算法、APIT定位[5,6]算法等一系列定位算法被提出.

无线传感器网络定位算法的分类[7]有多种,依据是否需要测量距离可分为测距算法和非测距算法,依据定位信息是否需要汇集到一个中心进行处理可分为分布式算法和集中式算法,依据网络中节点是否移动可分为动态定位算法和静态定位算法.Hu和Evans提出的MCL[8]算法是一种非测距、分布式和动态的定位算法,该算法为无线传感器网络的移动节点定位提供了新的思路,克服了文献[3-6]对网络拓扑变化的不适应性,能在连续的节点移动定位过程中降低能耗、减少累计误差和提高位置取得的响应速度.

当前,国内外学者对MCL算法的改进主要集中在以下几个方面:如何预测节点下一时刻的速度、如何缩小采样区域以及如何减小累积误差.针对节点运动预测,利用插值法[9,10]、最小二乘曲线拟合[11]、航位推测[12]、灰度预测[13]、小波变换预测[14]等,对节点下一时刻的速度和方向进行预测,提高采样效率.针对缩小采样区域,主要的方法有构建锚盒和采样盒[15,16]以提高采样成功率,提出负约束概念[17]排除非邻居锚节点通信范围内的采样区域,构建RSSI测距模型[18]限制采样区域,结合APIT算法[19]缩小采样区域等.针对累积误差修正,采用基于爬山策略的混合粒子群优化算法[20]减小定位整体误差.

但是,大部分学者对MCL算法在障碍物较多的定位场景中的适应性研究较少.针对这一问题,本文把障碍物抽象成节点,构建数学模型模拟障碍物对锚节点信号遮蔽的影响,通过对节点待定位前后锚节点信息的对比和两者位移关系的限定,恢复被遮蔽干扰信号的锚节点对样本滤波的作用,以此提高MCL算法在障碍物环境中的定位精度.

2 MCL算法分析

MCL算法的核心在于通过重要性采样的迭代更新,利用离散的加权样本去估计节点位置的后验概率密度分布.算法主要步骤包括预测阶段和样本过滤阶段,具体定位流程如下:

1.初始化采样.待定位节点在算法初始化时没有位置的历史数据,只能在节点部署平面内随机采集N个样本.初始化后,算法重复预测和样本过滤步骤.

2.预测阶段.以待定位节点t-1时刻的有效样本为圆心,vmax为半径作圆,在圆内采集样本,预测其在t时刻的位置.

3.样本过滤阶段.以待定位节点在t时刻观察到的锚节点信息为条件,滤除不满足条件的采集样本.

4.重采样和位置计算.采集的样本被过滤后,如果数目不满足预设的值,进行重采样.否则取样本集的质心为未知节点的估计位置.

MCL算法及其大多数改进算法均未考虑障碍物的影响,而现实场景中障碍物的出现会引起信号的衰减,进而降低算法的定位精度,因此有必要研究如何检测障碍物并有效降低障碍物对定位的影响.

3 障碍物对锚节点信号遮蔽的数学建模

为便于理解障碍物对锚节点信号传播的影响,同时构建算法的仿真环境,本节就障碍物对锚节点信号的影响进行建模.

将无线传感器网络中的障碍物抽象成与锚节点s和待定位节点p一样的节点b,b∈B,B为障碍物集合.取b影响范围参数为W,记锚节点s与待定位节点p的欧几里得距离为L,φ为高斯噪声,以W+φ为宽和L+φ为长构成一个矩形区域,如图1所示,只要b进入该矩形区域,则s成为p无法检测到信号的盲节点.

图1 障碍物影响区域Fig.1 Area affected by obstacles

记锚节点s的坐标为(xs,ys)、待定位节点p的坐标为(xp,yp)、障碍物节点b的坐标为(xb,yb),s与p的质心c的坐标为(xc,yc).设s与p确定的直线为l.

1)l与x轴垂直.障碍物影响区域为直线(1)所围成的矩形区域,如图1(a)所示.满足(2)式,则对于p,s的信号被遮蔽.

(1)

∃b∈B,|xb-xc|≤(W+φ)/2∧|yb-yc|≤(L+φ)/2

(2)

2)l与y轴垂直.障碍物影响区域为直线(3)所围成的矩形区域,如图1(b)所示.满足(4)式,则对于p,s的信号被遮蔽.

(3)

∃b∈B,|xb-xc|≤(L+φ)/2∧|yb-yc|≤(W+φ)/2

(4)

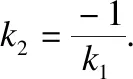
(5)

(6)

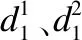
(7)

障碍物影响区域为直线(7)所围成的矩形区域,如图1(c)所示.满足(8)式,则对于p,s的信号被遮蔽.

(8)

4 BDMCL算法

在无线传感器网络中,记节点的最大运动速度为vmax,节点接收信号的半径为R,若节点在移动时不考虑信息的收发延迟,则BDMCL算法的定位流程如下:

4.1 初始化采样

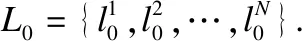
4.2 预测采样

(9)

4.3 找出盲节点

若p在以s为圆心R为半径的圆内,则称s为p的一跳锚节点;若p在以s为圆心R到2R之间的圆环内,则称s为p的二跳锚节点.

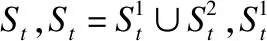
图2 锚节点与待定位节点的位移关系Fig.2 Displacement relation between anchor and node

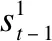
(10)

(11)

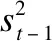
(12)

(13)

(14)

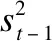
(15)

(16)

(17)

4)此外一个锚节点从pt-1的通信范围外变成pt的一跳或二跳锚节点,由于pt没有其历史信息,即使是被遮蔽了信号后被检测出来也没有充当指纹的作用.而锚节点从pt-1的一跳锚节点通信范围移动到pt的2R范围外,则由(17)式所排除,且其无法对pt的预测样本起到有效的正约束作用.

4.4 样本过滤

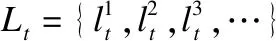
(18)

4.5 位置计算

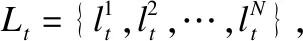
5 仿真分析

本文利用MATLAB平台,通过障碍物对锚节点信号遮蔽的数学模型构建算法运行的场景,对BDMCL算法进行仿真实验.待定位节点和锚节点移动模型为模拟运动轨迹更为平滑的Markov Waypoint Mobility Model[21],障碍物移动模型为模拟运动轨迹更为随机的Random Waypoint Mobility Model[21].若无特别说明,节点与障碍物均随机部署且自由运动.仿真实验的默认参数设置见表1.

表1 仿真实验默认参数
Table 1 Default parameters of simulation

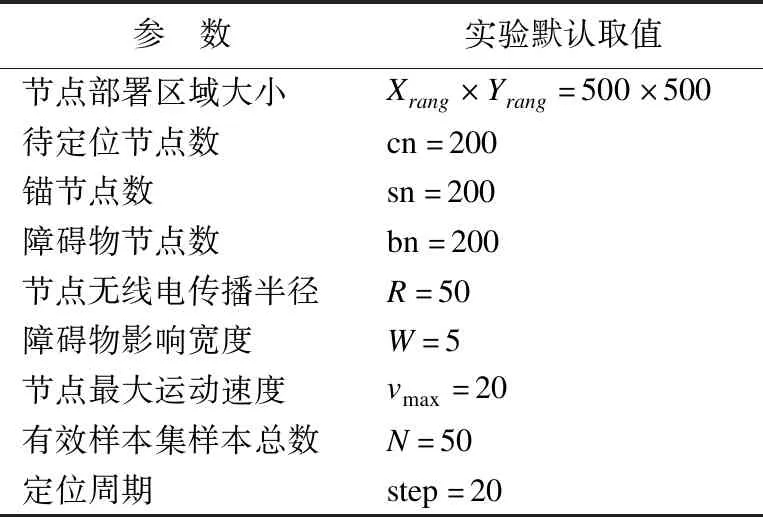
参 数实验默认取值节点部署区域大小Xrang×Yrang=500×500待定位节点数cn=200锚节点数sn=200障碍物节点数bn=200节点无线电传播半径R=50障碍物影响宽度W=5节点最大运动速度vmax=20有效样本集样本总数N=50定位周期step=20

仿真实验中每个待定位节点取20个连续的定位周期的均值作为仿真实验结果,记待定位节点的估计位置坐标为p(x,y),其真实位置坐标为p0(x0,y0),节点的位置坐标误差e的计算如式(19),e越小表明算法对节点位置坐标的估计越准确.

(19)

文献[9]提出的MCL改进算法IMCL(Improved MCL)是利用牛顿插值多项式对待定位节点的运动速度和方向作预测,以提高MCL算法采样的针对性.为验证新算法性能,本文对MCL、IMCL和BDMCL三个算法的定位周期、障碍物数目、节点运动速率和定位耗时的影响进行仿真实验.

1)定位周期

在20个定位周期中,待定位节点会出现收不到锚节点信号或采样失败的情况,从而造成节点定位误差的增加.BDMCL算法能对盲节点信号进行恢复,使得无锚节点信号次数与采样失败次数的均值较低.如图3所示,BDMCL无锚节点信号平均次数比MCL低44.50%,比IMCL低30.50%;采样失败平均次数比MCL低19.00%,比IMCL低4.50%.

由于BDMCL在障碍物环境的定位场景中利用盲节点信息加强了对预测样本的过滤作用,因而能够提高定位精度,如图4所示.在一个高度动态的定位场景中,由于待定位节点第一步无法依托历史信息,三种算法定位误差以及定位耗时均比较大,到了第二步,定位误差与定位耗时迅速收敛趋稳.经计算BDMCL比MCL误差平均低8.26%,比IMCL低10.10%.

2)障碍物数目

自由移动的障碍物数目发生变化时对定位误差也会产生一定的影响.如图5所示,障碍物数目的增加对定位耗时的影响较小,但障碍物的随机运动对BDMCL的影响较小,其平均定位误差比MCL低6.15%,比IMCL低16.69%.由于障碍物对定位精度的影响较为随机,BDMCL并未全线比MCL算法误差低,但误差最多仅高0.05R,误差的方差为0.0013,比MCL的0.0113和IMCL的0.007低.

3)节点运动速率

节点运动速率增大,待定位节点和锚节点指纹的相对位移关系变得不稳定,造成锚节点指纹与当前锚节点信息冲突,导致采样失败,造成定位误差的增大.如图6所示,BDMCL平均定位误差比MCL低10.64%,比IMCL低10.31%.

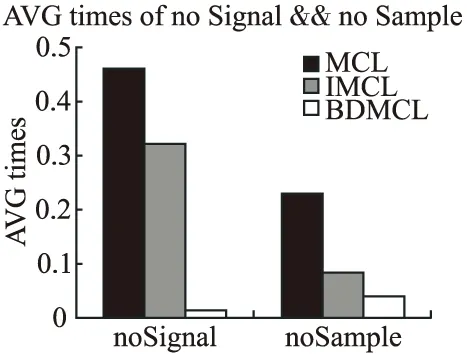
图3 待定位节点无锚节点信号与采样失败平均次数Fig.3 Average times of noSignal and noSample

图4 定位周期与定位误差的关系Fig.4 Relationship between positioning period and positioning accuracy

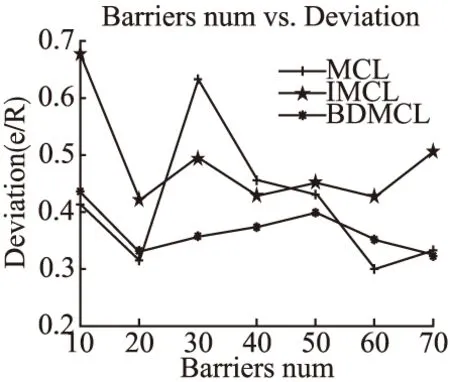
图5 障碍物数目与定位误差的关系Fig.5 Relationship between the obstacles and positioning accuracy

图6 节点运动速率与定位误差的关系Fig.6 Relationship between the velocity and positioning accuracy

4)定位耗时

BDMCL算法的采样方式与MCL算法一致,因此其定位耗时与MCL算法基本持平.而IMCL算法没有利用上一时刻的有效样本进行预测采样,牛顿插值多项式的预测在vmax较大时误差较大,导致采样耗时较大.如图7所示,BDMCL定位耗时比MCL高0.70%,比IMCL低44.70%.IMCL算法不适应于高度动态的定位场景.

5)障碍物固定且均匀分布

障碍物随机部署和移动时,BDMCL算法具有较好的性能表现.为分析障碍物均匀固定分布时,BDMCL算法是否依然能取得优势,本文也对障碍物固定且均匀分布的场景进行了实验.结果显示,BDMCL算法依然能有效利用盲节点的信息,取得比其余两种算法更好的定位精度.如图8所示,BDMCL定位误差平均比MCL低17.60%,比IMCL低14.91%.由于障碍物固定且均匀分布,减少了随机部署和移动的干扰,因此固定部署时,BDMCL定位误差比随机部署更低.

6 结 论

MCL算法是适用于无线传感器网络的移动节点定位算法,该文讨论了MCL算法在障碍物环境中的一种适应性解决方案.通过构建数学模型模拟障碍物对锚节点信号遮蔽干扰的影响,提出以待定位节点前后锚节点信息的对比和两者位移关系的限定的方法,恢复被遮蔽干扰信号的锚节点对其样本滤波的作用,以此提高MCL算法在障碍物环境中的定位精度.通过实验仿真对比,该文提出的BDMCL算法在障碍物较多的场景中能以较小的时间代价取得更好的定位精度.