一种基于深度网络的少样本学习方法

余 游,冯 林,王格格,徐其凤

(四川师范大学 计算机科学学院，成都 610101)

1 引 言

近年来，深度学习在机器学习、模式识别研究领域取得了巨大的成功[1].但在深度学习建模或模型迁移的过程中需要花费大量的代价来标记样本.少样本学习算法能有效地解决建模或模型迁移过程中标注代价大的问题，它的优点是只需要少量的标记样本就能建立较高识别率的模型.目前，小样本学习已成为机器学习领域的研究热点，引起了众多学者的广泛关注[2-9].

现有的少样本学习方法，大致可分为三类：一类是基于微调(Finetune)的方法，这类方法是利用已经在特定源域内训练的模型，通过在目标数据域上进行微调，以提高模型的泛化能力[2]；二类是基于测量的(Metric)方法，这类方法是对样本间距离分布进行建模，使同类样本相似度高，异类样本相似度低.其中主要的模型有孪生网络 (Siamese Neural Networks)[3]、匹配网络(Matching Networks)[4]、原型网络 (Prototypical Networks)[5]、关系型网络(Relation Network)[6]等；另一类是基于元学习(Meta-learning)的方法，这类方法是在现有的机器学习任务中学习元数据，试图利用元数据建立一种针对不同类型的学习问题都具有很好效果的模型.这类模型有递归记忆模型 (Memory-Augmented Neural Networks)[7]、模型无关自适应(Model-Agnostic)[8]等.

以上模型在源域和目标域(在少样本学习中源域可视为训练集，目标域可视为支持集和测试集)分布差异不大的Omniglot[10]数据集上表现都很不错，平均识别率均能达到99%左右[2-8].然而在源域和目标域分布差异很大的MiniImagenet[4]数据集上表现较差，识别率大概均在50%左右.这类模型还存在一个问题，当源数据做一点小的变化(例如随机调换源域和目标域中的种类)，模型的识别率会产生较大变化，说明模型对数据敏感.为了解决这些问题，本文提出了一种基于深度网络的少样本学习方法DL-FSL(Deep Learning-based Few-Shot Learning，DL-FSL).首先，将一个数据集划分为训练集、支持集、测试集，并利用有放回的随机采样方式从原始训练集中产生不同的训练集.其次，针对每个训练集，分别产生不同的样本集和查询集.然后，采用关系型深度网络[6]和Pytorch深度学习框架在不同的样本集和查询集上训练出不同基分类模型.最后，采用概率投票模型融合不同的基分类模型.实验结果表明，与文献[4-8]相比，DL-FSL方法在源域和目标域分布差异很大的情况下能有效地提高少样本学习算法的识别率.

本文的组织结构如下：第2节介绍了相关理论基础；第3节详细描述了本文DL-FSL方法；第4节对DL-FSL方法做了两组实验，并给出了实验结果与分析；最后对全文进行了总结.

2 相关理论基础

2.1 问题定义

为了方便叙述，首先我们用数学定义形式化与本文相关的基本概念.

定义1(数据集)：一个数据集D是一个三元组D=(X,Y,f)，其中：

X={x1,x2,…,xn}是n个输入实例观察值集合，本文中，∀xi∈X,xi表示输入的一个图片实例.

Y={y1,y2,…,ym}是m个类别标签集合.

f:X→Y是一个信息函数，它指定X中每一个输入实例的类别标签值，即对∀xi∈X，∃yj∈Y，有f(xi)=yj成立(i=1,2,…,n;j=1,2,…,m).

定义2(类标签实例集)：给定数据集D=(X,Y,f)，∀yj∈Y，若f-1(X|yj)={xi∈X|f(xi)=yj}，则称f-1(X|yj)为数据集D下的类别标签yj的实例集(i=1,2,…,n;j=1,2,…,m).

定义3(训练集、支持集与测试集)：给定数据集D=(X,Y,f)，以及参数C、K，随机生成D的三个子集Ts=(Xs,Ys,f)、Su=(Xu,Yu,f)、Te=(Xe,Ye,f)，如果满足：

①Yu=Ye，且Yu∩Ys=∅，Yu∪Ys=Y；

②Xu∩Xe=∅；

③|Yu|=C，其中|·|表示集合的势；

④∀yi,yj∈Yu,|f-1(Xu|yi)|=|f-1(Xu|yj)|=K.

则称集合Ts、Su、Te分别为D上的训练集、支持集与测试集.

定义4 (样本集与查询集)：给定训练集Ts=(Xs,Ys,f)，以及参数C、K，设Sa=(Xa,Ya,f)和Qr=(Xr,Yr,f)为Ts的两个子集，如果满足：

①Ya=Yr，|Ya|=|Yr|=C；

②∀yi,yj∈Ya,|f-1(yi|Xa)|=|f-1(yj|Xa)|=K；

③Xa∩Xr=∅；

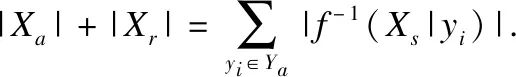
则称Sa、Qr为训练集Ts上的样本集和查询集.

定义5(C-way，K-shot少样本学习)：给定数据集D=(X,Y,f)，及参数C、K，根据定义3，划分出训练集Ts、支持集Su、测试集Te.给定任务：利用训练集Ts训练出一个分类模型，它能在支持集Su的支持下较好应用于测试集Te.称这个任务为C-way，K-shot少样本学习.

特别的，当K=1时，称此类任务为单样本学习(One-Shot Learning)，每个样本只需要给出一个实例样本，建立出的分类模型就能达到较高的识别率.当K=0时，称为零样本学习(Zero-Shot Learning).对于零样本学习，需要借助属性特征作为支持集，将其转化为一种特殊的One-Shot Learning.

2.2 深度卷积神经网络

2006年，Hinton团队[11]提出了深度置信网络的训练方式，随着十几年的发展，深度学习网络已经在图像识别、语音识别、文本处理等领域中取得巨大的成功.卷积神经网络(Convolutional neural networks，CNNs)[12]是深度网络中经典的学习方法，它包括卷积层和池化层.卷积层由若干个卷积核组成，通过对输入矩阵进行卷积操作，可提取出输入矩阵的不同特征.研究表明，前面几层卷积层只能提取出一些浅层特征，随着网络深度的加深，提取出来的浅层特征会慢慢组合成深层特征.池化层是一个采样层，常用的有平均池化层和最大池化层，其主要目的是对输入特征进行压缩，提取出主要特征.卷积公式和池化公式如下：

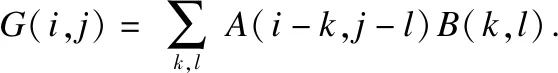
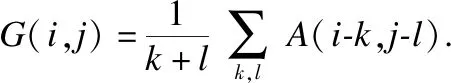
CNNs还有两个很重要的概念就是激活函数和损失函数.激活函数是用来加入非线性因素的，提高神经网络对模型的表达能力，常用的激活函数有Sigmoid 函数、tanh 函数、ReLU函数等.损失函数L是用来评估模型预测值Y′与真实值Y之间的差异程度.网络的训练过程，就是通过梯度下降法回传损失函数的值，然后相应调整模型的参数，使损失函数达到最小的过程.

3 本文DL-FSL方法

DL-FSL方法的流程如图1所示，它分成关系型网络和Bagging模型两个部分.本文先对两个部分的内容进行介绍.然后，再对DL-FSL方法进行详细描述.

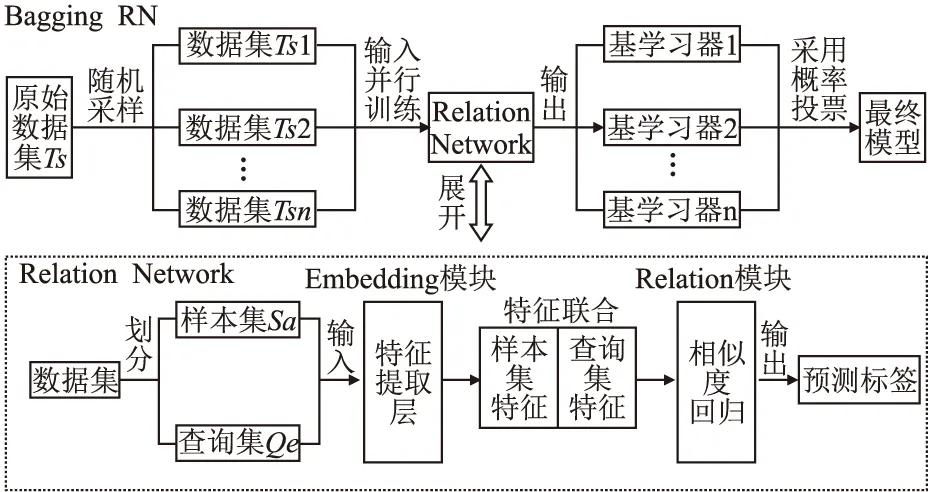
图1 DL-FSL方法流程Fig.1 DL-FSL method flow

3.1 关系型网络

关系型网络(Relation Network)[6]是一个深度卷积神经网络学习器，其网络结构包括两个模块：一个embedding网络模块用于提取图像特征，其中包含卷积层、池化层、卷积层、池化层、卷积层、卷积层共6层网络；一个relation网络模块用于回归图片的相似度，其中包含卷积层、池化层、卷积层、池化层、全连接层、全连接层共6层网络.本文所有网络的池化层均为最大池化层，具体网络结构及其参数见图2.

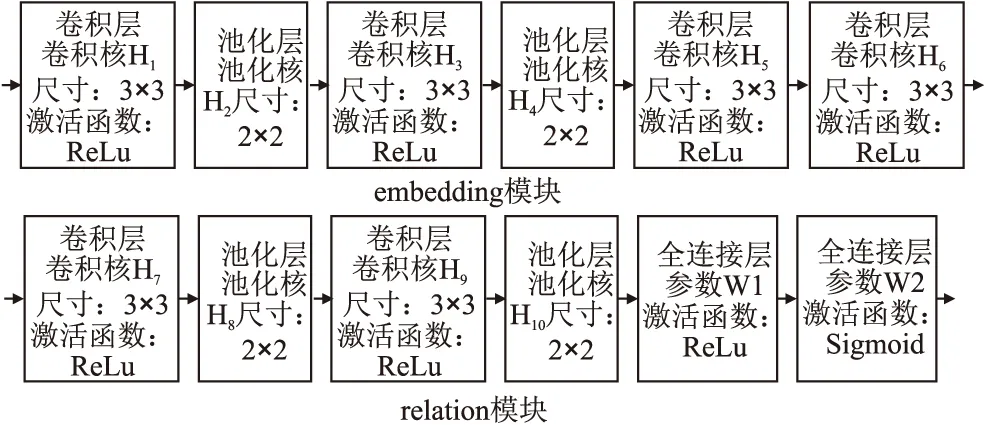
图2 embedding与relation网络结构图Fig.2 Embedding and relation network structure

关系型网络的基本思想是：首先，利用embedding网络模块分别提取出样本集Sa与查询集Qr的图像特征ξ1,ξ2；其次，利用relation网络计算出ξ1,ξ2之间的相似度，其值代表着每个样本集的图片实例与每个查询集的图片实例的相似程度，取出与查询集图片实例相似度最高的类别标签作为当前样本集的图片实例的预测标签；最后，采用真实标签与预测标签的均方误差作为整个网络的损失函数，利用梯度下降法进行训练.

3.2 Bagging模型

集成学习是利用多个基学习器解决同一任务，以提高模型的泛化能力[13]，它已被运用到机器学习的多个领域[13-16]，并取得了很好的效果.集成算法需要解决两个关键问题：一是如何构建具有差异性的基学习器；二是如何融合基学习器.研究表明，Bagging模型可以显著提高不稳定基学习器的泛化能力.结合少样本学习算法对数据敏感的特性，本文采用Bagging模型来提升深度网络的泛化能力.它的主要思想是：在训练阶段，通过有放回的随机采样(Bootstrap Sampling)产生很多不同的训练集，分别训练出不同的基学习器；在模型融合阶段，采用投票方式(常见的有简单投票、加权投票、概率投票等方式)对基学习器进行整合.

3.3 DL-FSL算法描述

DL-FSL算法描述如下：

算法1.DL-FSL方法

输入：数据集D=(X,Y,f)以及参数C、K、N、Times、θ； //C代表分类种类，K代表每个种类的样本数，N代表集成规模，Times代表最大训练次数，θ代表损失函数收敛的一个阈值.

输出：少样本分类模型Ω′.

Step 1.根据定义3，从数据集D中划分出训练集Ts、支持集Su、测试集Te；

Step 2.Fori=1 ToN

2.1.声明一个与训练集Ts大小相同的集合Ts i；

2.2.Forj=1 To |Ts|

2.2.1.随机复制Ts中一张图片实例Xsi到集合Ts i中；

End For

2.2.2.建立一条异步线程Syi，将步骤(2.3-2.11)的代码都放入异步线程中执行；

2.3.随机初始化模型Ω中所有网络层的参数；

2.4.取出训练集Tsi，根据定义4，随机划分出样本集Sa和查询集Qr；

2.5.取出样本集Sa中所有图片实例集Xa作为输入，输入到关系型网络模型Ω中embedding网络模块中.按照图2的结构图计算Xa的图像特征ξ1：

2.5.1.temp=ReLU (Xa⊗H1)

2.5.3.temp=ReLU (temp⊗H3)

2.5.5.temp=ReLU (temp⊗H5)

2.5.6.ξ1=ReLU (temp⊗H6)

2.6.取出查询集Qr中所有图片实例集Xr，按照步骤2.5.的方法计算Xr的图像特征，记为ξ2；

2.7.将ξ1,ξ2拼接成一个联合特征矩阵ξ，输入到模型Ω中的relation网络模块中.按照图2的结构图计算每张图片与查询集每类图片的相似度η：

2.7.1.temp=ReLU (ξ⊗H7)

2.7.3.temp=ReLU (temp⊗H9)

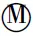
2.7.5.temp=ReLU (temp·W1)

2.7.6.η=Sigmoid(temp·W2)

2.8.η是一个高维矩阵，其每一行中的每一个元素，代表着样本集中的一个样本实例与查询集中一个类别的相似度，取每行最大相似度所对应的类别为该样本图片实例的预测标签，记所有图片实例的预测标签为Y′，其真实标签为Y；

2.9.采用均方误差MSE(Y,Y′)作为整个Relation Network的损失函数L；

2.10.If((Times>0)‖(MSE(Y,Y′)>θ))

2.10.1.Times=Times-1

2.10.2.利用梯度下降法反向传播L的值，以调整模型Ω中的参数；

2.10.3.转至步骤2.5.，继续训练网络参数；

End If

2.11.输出当前训练完毕的网络Ωi；

End For

Step 3.采用概率投票模型，融合基模型Ω1,Ω2,…,Ωn，得到最终少样本分类模型Ω′；

Step 4.输出少样本分类模型Ω′，算法停止.

上述DL-FSL算法的主要思想是：首先，采用随机采样方式产生N个具有差异性的独立的数据集；其次，建立N条异步线程，在异步线程中使用关系型深度网络并行训练出N个不同的基分类模型；最后，采用概率投票的方式融合不同的基分类模型.

4 实验及结果分析

为了验证本文DL-FSL方法的效果，实验分成实验1与实验2两个部分：实验1将DL-FSL和现有少样本学习方法的分类效果进行了对比实验；实验2分析了DL-FSL分类效果与集成规模N的关系.

实验数据集的选择：miniImageNet和Omniglot是研究少样本学习算法的两个经典的公开数据集.miniImageNet[4]数据集含有100个常见物种，每个物种之间的差异性很大，例如麻雀和卡车，每个物种有600张图片，总共60000张.Omniglot[10]数据集包含来自 50个不同字母的1623个不同手写字符.每一个字符都是由20个不同的人通过亚马逊的Mechanical Turk在线绘制的.

本文实验采用的硬件环境为NVIDIA Tesla K80 GPU平台；软件环境为Linux系统、Python编程语言、Pytorch深度学习框架.

4.1 实验1 ：DL-FSL方法分类效果验证

实验1的主要目的是测试DL-FSL方法的分类效果.因此，给出了DL-FSL方法与目前公开的少样本学习方法的实验对比.实验参数的设置与文献[4-8]中相同，也采用C=5，K=1和C=5，K=5的情况下进行实验.

实验步骤如下：

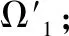
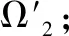
4.1.1 Omniglot数据集实验结果

将Omniglot数据集划分成训练集1200类，支持集与测试集423类.按照实验一的步骤进行实验，并增加20 way 1 shot、20 way 5 shot的参数设定，实验结果如表1 所示.从表1中可以看出，对于Omniglot数据集，在5 way 1 shot、5 way 5 shot、20 way 1 shot、20 way 5 shot参数设定下，本文DL-FSL方法的准确率均超过了其它主流的少样本算法的准确率.尤其是在20 way 1 shot参数设定下，DL-FSL方法的准确率(98.8%)比Relation Nets的准确率(97.6%)高出了1.2%.

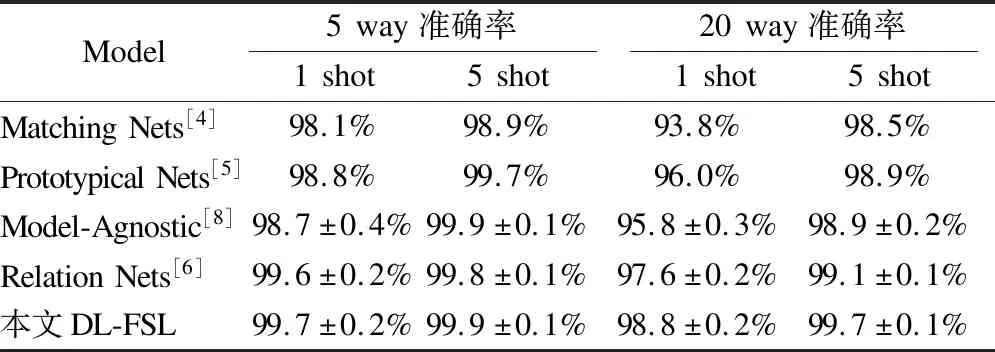
表1 Omniglot数据集下DL-FSL方法与目前主流少样本学习方法准确率对比Table 1 DL-FSL method compared with other FSL method in Omniglot dataset

4.1.2 miniImageNet数据集实验结果

将miniImageNet数据集划分成训练集64种，验证集(包含验证时的支持集与测试集)16种，支持集与测试集20种.按照实验一的步骤进行实验，结果如表2所示.从表2中可以看出，5 way 1 shot设定下，DL-FSL方法的准确率达到了52.06±0.82%，比Relation Nets(50.44±0.82%)的准确率高出了1.62%，且超过了现有主流的其它少样本算法；5 way 5 shot设定下，DL-FSL方法的准确率达到了67.75±0.70%，比Relation Nets(65.32±0.70%)的准确率高出了2.43%，除了略低于Prototypical Nets(68.20±0.66%)，也均超过了其它主流的少样本学习算法.实验结果说明了DL-FSL方法对少样本学习算法具有很好的提升效果，也说明通过DL-FSL方法确实能提高少样本学习算法模型的泛化能力.

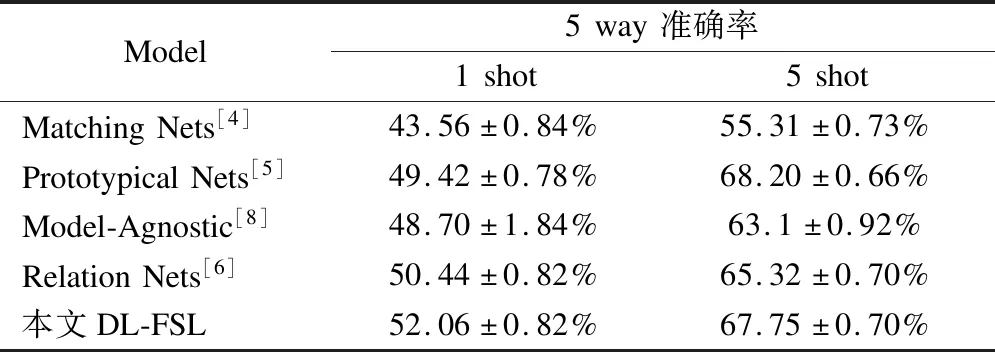
表2 miniImageNet 数据集下DL-FSL方法与目前主流少样本学习方法准确率对比Table 2 DL-FSL method compared with other FSL method in miniImageNet dataset

4.2 实验2：DL-FSL分类效果与集成规模N的关系

实验2的主要目的是为了研究DL-FSL分类效果与集成规模N的关系.从表一中可以看出在Omniglot数据集下，DL-FSL的准确度提升空间太小.因此，我们采用miniImageNet数据集来研究DL-FSL的分类效果与集成规模N的关系，将N从1取到10，分别在5 way 1 shot和5 way 5 shot下，按照实验1的步骤进行对比实验.

实验步骤如下：

Step 1.Fori=1 To 10

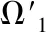
实验结果如图3所示.

图3 DL-FSL分类效果与集成规模N的关系图Fig.3 relationship between DL-FSL′s classification effect and ensemble scale N

从图3中可以看出，随着集成规模N的增加，集成效果越来越好.当集成规模N=3时，5 way 1 shot和5 way 5 shot的集成效果均可达到原始的Relation Network的准确率.当集成规模N>7时，随着集成规模的增加，集成效果涨幅越来越小.当集成规模N超过10时，集成效果开始收敛于一个值，从而也验证了周志华教授在文献[17]的观点，集成器不是越多越好.

5 结 论

少样本学习是机器学习中的难点与热点.它能在标记样本很少的情况下，学习出识别率较好的机器学习模型.然而现有的少样本学习算法在源域与目标域样本分布差异很大的情况下，学习出的模型泛化能力不强.本文首先用数学定义形式化地描述了少样本学习相关概念.然后，提出了一种DL-FSL方法并给出了详细的算法描述.最后，将本文DL-FSL方法与现在主流少样本学习方法做了两组对比实验.实验结果证明了本文DL-FSL方法能有效地提高模型的泛化能力.下一步工作，我们将把本文DL-FSL算法应用在数据集自动标注上，有效解决深度学习在建模或模型迁移过程中需要花费大量的代价来标记样本的问题.