一种基于社会选择的本体聚类与合并机制
2019-06-06朱俊武朱泽宇
滕 玲 ,朱俊武 ,李 斌,2 ,杨 洲,朱泽宇
1(扬州大学 信息工程学院,江苏 扬州 225009)2(南京大学 软件新技术国家重点实验室,南京 210093)3(扬州大学 广陵学院,江苏 扬州 225000)
1 引 言
随着web技术的不断发展,语义web为网页扩展了计算机可理解的、可处理的语义信息,从而解决了因信息形式异构、语义多重性带来的机器之间无法理解和交互的问题[1].知识图谱是大数据的结构化表示,作为互联网资源组织的基础,能够促进语义web的发展.本体是对特定领域中概念及概念之间关系的形式化表达,可以作为知识图谱表示的概念模型和逻辑基础.因此在语义 web中,本体可以为web上的信息提供语义解释,有利于人机交互[2].然而随着特定领域的扩大和本体数量的剧增,不同用户或agent根据不同需求、应用来构建本体,他们往往采用不同的建模方式或本体描述语言,但这些本体所描述的内容在语义上有时会有重叠或者关联,这就造成了本体的异构.由于分布式本体异构的特性阻碍了web服务的互操作性,使之成为了语义web中亟待解决的问题之一[3].本体映射(Ontology mapping)和本体合并(Ontology merging)都能有效的解决上述问题.本体映射是将源本体通过映射规则转换成目标本体的过程,它侧重于发现两个本体中术语或概念之间的语义关联,本体映射不会改变源本体的结构;而本体合并是指在给定一组源本体的基础上,通过预先定义好的合并规则生成一个新的共享本体,新本体能够为具体语义提供一个共享的词汇表,但这个新本体相对于源本体结构上发生了改变[4].
具体来说,本体合并是将特定领域中n(n≥2)个异构的局部本体(Individual local ontology)合并成一个新的共享决策本体(Shared collective ontology)的过程,因此我们可以将此过程看成是社会选择理论(Social Choice Theory,SCT)中的一种应用.社会选择是经济学的一个重要分支,主要研究和分析个体偏好和社会决策之间的关系,并为聚集个人偏好提供了多种聚集规则和评判准则.近年来,众多学者将SCT与计算科学领域相结合,从而形成一门新的交叉学科“计算社会选择”,在涉及聚集个体偏好的领域有着广泛应用[5].例如,社会选择函数在多智能体系统(Multi-agent system)和推荐系统(Recommender system)等方面有着举足轻重的意义.投票理论(Voting theory)和判断聚集(Judgement aggregation)作为社会选择的经典应用为本体合并奠定了理论基础,其中常见的聚集方式以及一般性质,例如一致性、单调性、中立性等都为本体合并机制的设计提供了方法论.
基于以上,本文从SCT的角度出发,综合考虑本体构建者的可信度和本体间的相似度,针对异构源本体的合并问题做出研究.文章的主要架构如下:第二部分介绍国内外学者对本体合并的研究现状以及存在的不足之处;第三部分构建了以社会选择和描述逻辑为基础的本体合并框架,并给出了相关的定义和公式;第四部分具体阐述了本体合并机制中的两个关键技术,本体聚类和本体聚集(包括积分规则和阶梯规则)的具体算法及其相关性质;第五部分采用应用案例和对比实验验证了本文所提出的合并机制的有效性;第六部分针对目前工作存在的问题作出总结并对规划了未来的工作方向.
2 相关工作
为了促进语义web的发展,国内外学者对本体映射、本体集成等相关问题做出了大量研究并取得了较为满意的成果.其中,比较成熟的本体合并系统有PROMPT[6],FCA-Merge[7],Chimaera[8]和SMART[9]等.PROMPT是一种用于提供本体半自动化映射与合并的算法,能够对本体的类、属性及其关系进行合并;FCA-Merge是一种自底向上的合并方式,运用自然语言处理和形式化概念分析,在人工交互的基础上完成本体合并;Chimaera是支持本体合并和不一致性诊断的系统,它能识别不同源本体中具有相同语义的概念和概念之间的关系.SMART是一种不受平台限制的基于通用知识模型的合并系统,在合并的基础上增加了对本体不一致性的检测,并给出了修复这些不一致本体的方法.然而这些系统都需要人工参与才能完成,费时又费力,尤其是当源本体数量过大时,系统可能无法精确的对其进行合并.Wang[10]对现有的本体映射方法进行了分类与总结,认为基于机器学习的本体映射技术能较好的解决由于本体规模不断激增给本体映射带来的问题.在文献[11]中,作者将概念代数相关理论应用于本体合并当中,并提出了FCA-OntMerg方法.这种方法首先将本体规范化成统一的概念代数表示形式,再根据严格的概念格准则进行合并以生成一个新本体,实验结果验证了该方法在解决本体异构问题上的有效性.唐杰等人[12]将映射问题转化为风险决策问题,以贝叶斯决策为理论设计了风险最小化的本体自动映射模型,实验证明了该方法具有更高的查准率和查全率.
在社会选择理论方面,投票理论的发展和判断聚集的进步都为本体合并奠定了基础[13,14].投票理论是将投票者的个体偏好聚集为集体偏好的过程,在投票过程中要平等对待每个候选者,做到“公平公正公开”,常见的投票聚集方式包括Borda规则、k-赞成投票规则、单记移让式投票等[15,16].Borda计数法和赞成投票制都是较为简单的聚集方法,每个候选项根据选票的数量来确定最终的赢者.单记移让式投票较为复杂,每一轮中都会淘汰得票数最少的候选者,最后未被淘汰的候选者即为赢者,在此过程中所有的选票在每一轮的计票中都会被计算到.文献[17]借助工具OntoCmaps提出了以图论为基础的投票机制,探讨了在本体学习中概念检测的问题.Dietrich F[18]和Pigozzi G[19]致力于研究如何将一群个体对命题的判断聚集为一个集体决策,即判断聚集.在判断聚集中既要保持聚集过程中的公平性,又要关注聚集结果的正确性,并由此提出了多种聚集方式,如基于前提/结论的方法、基于距离的聚集过程等.然而这些聚集方式均要兼顾公平、公正的性质,需要平等的对待每个候选者并假设所有投票者拥有的背景知识相同,这点在本体合并中并不适用,因为每个本体构建者对领域知识的认知程度并不相同.
3 本体合并框架
本节主要阐述基于社会选择的本体合并框架,首先在3.1节介绍描述逻辑及问题模型所需的定义和概念,在3.2节中描述合并框架的组成部分和具体流程.
3.1 问题描述与基本定义

现给定一组有限的候选公式集合Φ和专家(本体构建者)集合AgentN={1,2…n},其中每个agenti∈N都可以根据自身的知识或经验构建一个具有一致性的本体,记为Oi⊆Φ.用CO表示所有具有一致性的本体集合,此集合中不仅包含了O1,O2…On,还包含了其他未被agent所构建但具有一致性的本体.本文将O=(O1,O2,…On)∈CON称为一个本体组合.由于每个构建者的背景知识和对领域认知程度不同,本文创新性地为每个构建者都设置了可信度属性,可信度用符号ri∈[0,1]表示,由agenti所构建的本体Oi也具有相同的可信度,则R=(r1,r2,…,rn)表示本体组合的可信度向量.基于上述形式化表示,本文分别定义本体聚类和本体聚集两个概念:
定义 1. 本体聚类本体聚类是指根据本体的相似度将可信度相近的本体划分到一起.已知类别集合C和本体组合O,分类规则G:O→C能使任意Oi∈O经过映射后被划分到一个类Cj∈C中.
定义 2. 本体聚集定义本体聚集规则为将源本体组合O映射到一个共享的决策本体的过程,即F:CON→2Φ,经过聚集规则生成的决策本体F(O)未必具有一致性.
本文的主要研究思路是通过本体聚类算法舍去可信度较低的本体,从而降低其对合并精度的影响;再利用聚集规则对可信度高的源本体进行合并以生成一个共享的决策本体.精准的聚类算法能为本体聚集奠定良好基础,而对于本体聚集规则来说,本文希望能够得到一个具有一致性的共享本体.
3.2 本体合并流程
从社会选择的角度出发,考虑每个本体构建者的可信度和本体间的相似度,本文构建了如图1所示的面向可信度的异构本体合并框架,主要由三个部分组成,分别是本体聚类器和本体聚集器和决胜规则.本体聚类器是本体聚集的前提,舍弃低可信度本体从而为合并本体的精度提供了保障,它可以根据每个本体的可信度和本体间的相似度对其进行聚类;而本体聚集器则是通过某种聚集规则对源本体进行合并以期形成一个共享的决策本体;若经过聚集后有多个符合要求的本体则需要借助决胜规则来确定唯一F(O),本文不详细介绍此规则.
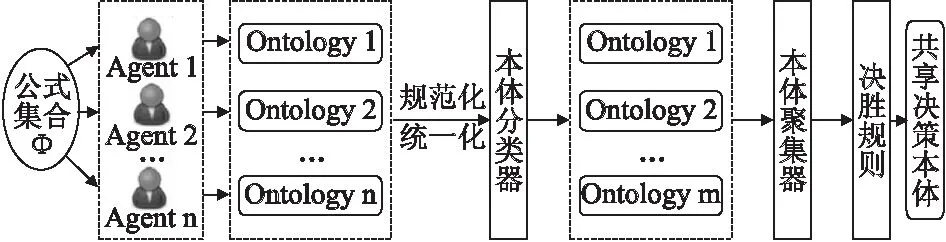
图1 基于社会选择的本体合并框架Fig.1 Framework for ontology merging based on social choice
根据图1所示的本体合并框架,本文所提出的本体合并机制具体的工作流程有如下几个步骤:
1)每位agent根据自己的经验和知识背景构建出特定领域的本体;
2)基于描述逻辑,将本体规范成统一的形式O=
3)本体分类器依据设定好的聚类算法和本体的可信度向量R对本体组合O中的源本体进行聚类,形成k个集合.为了便于计算,本文令k=2,设定了2个可信度集合,分别为高可信度集合OH和低可信度集合OL;
4)删除可信度低的本体集合OL,保留高可信度本体,令本体组合O=OH;
5)最后对高可信度本体组合O使用本体聚集器和决胜规则以生成唯一的共享决策本体F(O).
4 本体合并过程
对本体进行聚类有助于获得更准确的本体聚集结果,本小节将详细介绍本体合并框架中两个重要的组成部分,本体聚类器和本体聚集器.
4.1 本体聚类器
本体聚类器一方面要根据每个本体的可信度对其进行分类,目标是形成两类本体集合OH和OL,分别表示高可信度本体集合和低可信度本体集合;另一方面也要考虑本体之间的相似度,目标是将相似度高的本体划分为一类.为了衡量两个本体之间的相似度,现定义距离函数d:2Φ×2Φ→+∪{0}表示两个本体之间的距离,距离越小则表示两个本体越相似.常用的距离函数有海明距离、欧式距离和曼哈顿距离[21,22],他们都满足
1)非负性:d(Oi,Oj)≥0;
2)同一性:d(Oi,Oj)=0若Oi=Oj;
3)对称性:d(Oi,Oj)=d(Oj,Oi)
本文采用海明距离,即将本体Oi转化成Oj需要改变最少的公式个数.理想情况下,我们希望集合OH中的本体尽可能的相似,而异类本体尽可能不同.兼顾本体可信度和本体相似度,本文设计了异构本体聚类器,聚类算法具体流程如Algorithm 1所示.
算法1.Distance-based Ontology Clustering for Reliability
Input:O,R
Output:OH,OL
1OrderontologyprofileOintheascendingorderaccordingtoreliabilityvectorR

3λH=OλL
4repeat
5OH={ontologyOhwithhighestreliability}
6OL={ontologyOhwithhighestreliability}
7fori:1→ndo
8 compute the distance betweenOlandOidli;
9 compute the distance betweenOhandOidhi;
10if(dli≥dhi)then
11OH←OH∪{Oi}
12elseOL←OL∪{Oi}
13endif
14endfor
16Oh←Oh-1withthesecondhighestreliability
17endif
其中第1行是对本体集合进行初始化,将本体按照可信度进行升序排序.第2-3行根据可信度高低程度粗略的将本体分为两类,显然这样的分类是不够精确的因为没有考虑本体间的相似度.在第7-14行计算每个本体Oi与最高可信度本体Oh和最低可信度本体Ol的距离,并根据距离远近确定其所在的类.第15-17行表示,若存在大量可信度低的本体与Oh相似,则说明Oh可能不准确,因此选取可信度次高的本体作为类中心并进行迭代更新,直到OH中包含的本体可信度较高同时类内本体较为相似时则停止更新(第18行).
定理1.异构本体聚类算法的时间复杂度为O(n*log2n+nt),其中t是循环次数.
证明:根据本体可信度向量R,我们采用堆排序对本体集合中的n个源本体进行升序排序,时间复杂度为O(n*log2n).内循环(第7-14行)中分别计算本体Oi与类中心Oh和Ol的距离并确定其所在类别,共执行了3n次;在外层循环中,由于设置迭代次数为t,那么执行的频率为t*(3+3n);综上所述,算法的时间复杂度T(n)=O(n*log2n)+t(3+3n)=O(n*log2n)+O(nt)=O(n*log2n+nt).
面向可信度的本体聚类算法简单、直观,综合考虑了异构本体的可信度以及本体间的相似程度,减少了类中心本体选择不当对聚类结果造成的不利影响;但对于本体规模较大的情况,其时间和空间复杂度较高,还需要在后续工作中进一步优化.
4.2 本体聚集
借鉴社会选择理论中的聚集规则,本文对其进行总结与分类,并在原有的聚集规则之上兼顾本体可信度和本体相似度,形成了积分聚集规则和阶段性淘汰规则两种方式.
4.2.1 积分聚集规则
积分聚集规则通过函数score:CO→,将具有一致性的本体集合映射到一个实数集.每个一致性本体根据积分函数都可以获得某个得分,积分聚集规则的最终目标是将得分最高的本体作为共享本体,即
F(O)=agrmaxco∈COscore(CO)
在积分聚集规则中,最终生成的共享决策本F(O)体必然具有一致性.本文介绍两种积分聚集规则,分别是基于距离的得分规则和基于可信度的得分规则.
1)基于距离的得分规则
基于距离的得分规则将每个本体的得分定义为与本体集合O距离的相反数,即
score(CO)=-d(CO,O)=-∑i∈Nd(CO,Oi)
由上述公式可知,若score(CO)越大,则它与本体集合O的距离越小.换言之,CO与其他本体相似越高,更容易得到agent的认可;反之CO得分越低,与其他本体相似程度越低.
2)基于可信度的得分规则
最简单的基于可信度的得分规则定义每个本体的得分即为自身的可信度,将可信度最高的本体作为共享本体.显然这种得分规则过于简单且没有考虑CO中的其他本体.因为可信度高的本体构建者对领域认知也可能会出错,而可信度低的构建者也有可能构建出比较完备的一致性本体.为了解决上述问题,首先定义标志
用于判断本体Oi中是否包含公式φ;那么每个公式的可信度记为r(φ)=∑i∈Nri·xOi(φ).因此,基于可信度的得分规则将本体的得分定义为它所包含的所有公式可信度之和,即
score(CO)=∑φ∈COr(φ)
若CO的得分越高则表明该本体包含的公式可信度越高,这在一定程度上克服了直接选择可信度最高本体作为共享本体的弊端.
定理 2.当同等对待所有本体构建者,即ri=1对任意i∈N成立时,基于海明距离的得分规则就是基于可信度的得分规则.
证明:一方面,海明距离d(Oi,Oj)=|Oi|-|Oi∩Oj|定义为两个本体间相异公式的个数.那么,基于距离的得分规则可以表示为
Fdis(O)=argmaxco∈co(-∑i∈Nd(CO,Oi))
=argminco∈co∑i∈Nd(CO,Oi)
=argminco∈co∑i∈N(|CO|-|Oi∩CO|)
根据定义,基于距离的得分规则的最终目标是寻找能使∑i∈Nd(CO,Oi)最小的一致性本体,经过公式推理可以将原目标转换为求使得∑i∈N|Oi∩CO|最大的一致性本体.另一方面,当ri=1对任意i∈N成立时有
Frel(O)=argmaxCO∈CO(∑φ∈COr(φ)
=argmaxCO∈CO(∑φ∈CO∑φ∈NxOi(φ)
因此基于可信度的得分聚集规则目标是获得能使∑φ∈CO∑i∈NxOi(φ)最大的一致性本体.又因为|Oi∩CO|=∑φ∈COxOi(φ),所以命题得证.
例1.现有3个agent构成的本体组合O={O1,O2,O3},并且他们都共同认可Tbox中的公式:C3=C1∩C2.由于agent的背景知识和经验不同,对于Abox中的对象a也有不同的观点,如表1所示.根据Tbox中的约束条件,则一致性本体集合CO={CO1,CO2,CO3,CO4}.
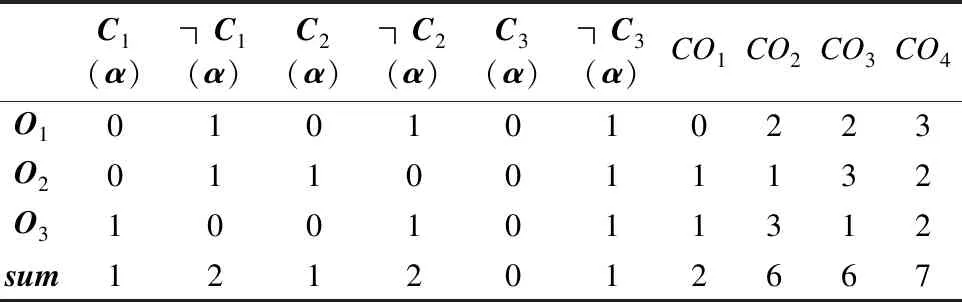
表1 本体及其得分Table 1 Formulas in ontologies and their scores
其中,CO1={Tbox∪{C1(a),C2(a),C3(a)}}
CO2={Tbox∪{C1(a),┐C2(a),┐C3(a)}}
CO3={Tbox∪{┐C1(a),C2(a),┐C3(a)}}
CO4={Tbox∪{┐C1(a),┐C2(a),┐C3(a)}}
首先根据xOi(φ),若本体中包含φ则记为1分,否则记0分.每个公式的可信度得分为r(φ)=∑i∈NxOi(φ),例如r(C1(a))=0+0+1.每个一致性本体的得分score(CO)=∑φ∈COr(φ),例如score(CO1)=1+1+0.可以发现,|Oi∩CO|=∑φ∈OxOi(φ),例如|O1∩CO1|=0+0+0=∑φ∈CO1xO1(φ).因此,Fdis(O)=Frel(O)={CO4}.
4.2.2 阶梯性淘汰规则
阶梯过程是一种经过多轮次筛选从而产生共享本体的聚集方式.由这种方式生成的共享本体未必具有一致性,需要通过某种约束来达到具有一致性的目的.为了使最终本体具有一致性,在每一轮中都保留具有可满足性的概念或断言;删除或修改不可满足的概念.
1)基于优先规则的多阶段淘汰制
基于支持度的优先规则:φψ⟺

基于可信度的优先规则:φψ⟺r(φ)≥r(ψ).
这种聚集方式首先根据上述定义的优先规则对Φ中的公式进行排序,接着在以后的每个阶段中都只考虑一个公式.首轮中考虑优先级最高的公式并将其加入共享决策本体F(O)中;然后再根据优先级依次考虑剩余公式,若添加当前公式至F(O)会导致已形成的决策本体不一致,那么删除或修改此公式,继续考虑下一个公式,直到遍历完所有的公式为止.我们可以将此过程用形式化语言表示,即F(O)是一个公式集合Δ⊆Φ满足以下条件:
1)Δ={φ|φ∈O1∪O2…∪On};
2){φ∈Δ|φψ}∪{ψ}是具有一致性的.
定理 3.基于优先规则的阶段淘汰制具有一致赞同性.
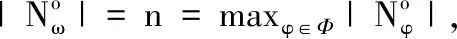
2)基于推理的两阶段法
本文将判断聚集中的基于前提(或结论)的聚集过程应用在本体当中,得到基于Tbox(orAbox)的本体聚集规则.这两种方式的主要步骤相似,这里只介绍一种基于Abox推理的本体聚集规则.在这之前先介绍两种较为简单、常见的聚集函数,分别是绝对多数规则和基于距离的聚集规则.绝对多数规则是指当接受一个公式φ∈Φ的agent个数超过半数时,φ会被最终结果接受,即
基于距离的聚集规则在3.2.1节中以介绍,这里不再赘述.那么,基于Abox推理的本体聚集规则具体的过程可用如下算法表示:
算法2.Abox-based Approach for Ontology Aggregation
Input:O1,O2,…,On
Output:O
1Abox←Ø
2fori:1→ndo
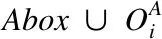
4i←i+1
5endfor
7forj:1→ndo

9repairontologyOjforconsistency
10endfor
11F(O)=argminCO∈CO∑i∈Nd(Oi,O)
第2-6行首先用绝对多数规则对本体组合中的Abox进行聚集,得出结果为FA(O);第7-10行中每个agent将源本体中的Abox改变为F(O),并根据本体一致性进行修正;最后对这些修正后的本体组合使用“基于距离的距离规则”以形成最终的共享本体(第11行).在本体不一致修正时分为两个步骤,首先找出最小不一致集合Δ={φ|φ∈Tbox},即Δ∪FA(O)具有不一致性;然后删除或修改集合Δ.当采用基于Abox的两阶段方法时,Abox和Tbox相互独立,对Abox中的公式运用绝对多数规则得到FA(O),而Tbox中的公式取决于FA(O).因此,一致赞同性对于Abox中的公式仍然成立,但Tbox中的公式未必满足.若希望获得具有一致赞同性的聚集规则,需要对其中的公式加以约束.
定理 4.令Tbox=T1∪{p}={a1,…,al}∪{p}且β∈Abox,当基于Abox的两阶段法满足约束xO(α1)∧…∧xO(αl)∧xO(p)↔xO(β)时具有一致赞同性.

①当β∈FA(O)时,根据算法2中第7-11行,得到β∈F(O),也就是xF(O)(β)=1,又因为xF(O)(α1)∧…∧xF(O)(αl)∧xF(O)(p)↔xF(O)(β),所以xF(O)(p)=1,命题得证.

∑i∈Nd(Oi,F(O))=
考虑这样一个本体F(O)′使得p∈F(O),xF(O)′(φ)=xF(O)(φ)对任意φ∈φ/{p}成立.那么
∑i∈Nd(Oi,F(O)′)=
这与∑i∈Nd(Oi,F(O))最小矛盾,因此假设不成立,原命题成立.
5 应用案例与分析
为了验证本文提出的本体合并机制的有效性,现假设所有agents都共同认可Tbox中的公式:C4=(C1∪C2)∩C3,C5⊆┐C4,C1,C2,C3,C4,C5分别表示5个原子概念.若存在论域中的一个对象a,那么Abox中的公式可被构建为C1(a),C2(a),C3(a),C4(a),C5(a).表1根据定义
将6个agents构建的Abox表示为0-1向量.

表2 6个构建者提供的本体断言集及可信度Table 2 Aboxes and reliabilities of 6 agents


图2 本体聚类器的分类结果Fig.2 Results of ontology clustering
将本文异构本体聚类算法和k-means聚类算法[23]进行比较.k-means算法随机选择k个样本作为初始点,以最小化平方误差为目的将每个点划入最近的簇,然后重新计算每个簇的均值直到簇不发生改变为止.令聚类簇数k=2,图3是仅针对本体间相似度进行分类的聚类结果,而图4是只考虑本体的可信度的聚类结果.
通过计算DBI(Davies-Bouldin Index)可以评判分类性能的好坏,DB指数越小,分类性能越好.我们从“本体可信度”和“本体相似度”两个属性来对上述3种分类结果进行比较,对比结果如图5所示.


图3 k-means聚类结果(本体相似度)Fig.3 Results of k-means for similarity图4 k-means的聚类结果(可信度)Fig.4 Results of k-means for reliability
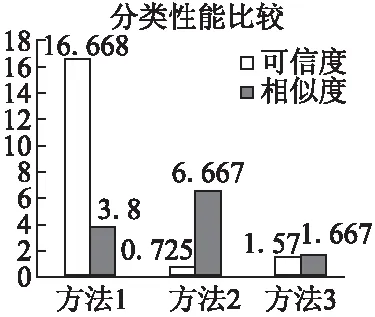
图5 分类算法性能对比结果Fig.5 Performance comparison of classification algorithm
方法1为仅考虑本体相似度的k-means聚类算法,方法2是仅考虑本体可信度的k-means聚类算法,而方法3是本文提出的兼顾可信度和相似度的本体聚类算法.通过对比可以发现,尽管本方法在可信度分类方面的性能不及方法2,但总体来说分类性能介于三者之间,能够很好的兼顾相似度和可靠性两个属性.
在本体聚类的基础上将置信度低的本体舍去,那么在本体聚集时O={O4,O1,O3}.根据Tbox中的约束条件,具有一致性的本体集合CO如表3所示.

表3 一致性的本体集合中的断言集Table 3 Aboxes of ontologies in CO
分别用积分规则和阶梯性淘汰规则对异构源本体进行聚集. 基于海明距离的积分规则得到的结果为F(O)={CO4}={O1},因为
score(O1)=-2=argmaxco∈CO(∑i∈Nd(CO,Oi))
基于置信度的积分规则得F(O)={O1},因为
score(O1)=7.05=argmaxco∈CO(∑φ∈COr(φ))
多阶段淘汰规则得到的结果为F(O)=CO4=O1,因为不论根据支持度或是可靠性都有C4(α)C5(α),所以优先考虑将C4(α)加入F(O)中,得F(O)={O1}.基于Abox的两阶段聚集法得到F(O)⊆{O1,O4},首先根据绝对多数原则得到FA(O)={C2(α),C3(α)},继而得到
∑i∈Nd(Oi,O1)=∑i∈Nd(Oi,O4)=1
=argminCO∈CO∑i∈Nd(CO,Oi)
若我们最终只想获得唯一的决策本体,那么需要在原有的聚集规则中结合决胜规则,这将是未来的研究方向之一.
6 总 结
本体合并是促进语义web发展的关键技术之一,为了解决目前存在的语义异构问题,以社会选择为理论依据,将不同agent构建的异构本体(个体偏好)通过本体合并机制生成一个顶层本体(集体决策)以期形成一个更大的语义共享空间.由于不同agent的背景知识不同,所构建的本体也具有不同的可靠性.因此,本文针对异构本体的可信度,设计了本体聚类器和本体聚集器,本体聚类器为本体聚集器缩减了本体聚集规模,从而提高了本体合并精度.然而还存在着一些不足之处使得这种合并机制无法在真实场景中应用.一方面,这种基于距离的本体分类器的时间和空间复杂度都会随着本体数量的扩大而剧增;另一方面,本体聚集器的设计中还未考虑社会选择中的其他重要性质,例如中立性、单调性和独立性等.未来的主要工作将致力于设计一种决胜规则和完善这两方面的不足以不断提升本体合并机制,并将此机制用于描述语义web服务,使具有计算机可理解的语义.
