基于PCA和改进TOPSIS法的电厂混煤配比方案综合评价
2019-12-04刘长良王梓齐
张 厚,刘长良,2,王梓齐
(1.华北电力大学控制与计算机工程学院,河北 保定 071000;2.华北电力大学新能源电力系统国家重点实验室,北京 102206)
受煤炭资源分布不均等不利因素影响,我国许多电厂煤炭供应较设计煤种出现了较大偏差,致使实际燃煤热效率低,锅炉结焦现象频发,对安全生产和经济运行产生了较大影响。因此,混煤掺烧就成为了保证锅炉运行的安全性、经济性和环保性的最佳选择。理想的混煤配比方式是将燃烧特性不同的煤种按特定比例混合,混合后的煤在着火特性、燃烧稳定性和结渣特性等方面都能达到或者尽可能接近设计煤种。
逼近理想解排序法(TOPSIS 法)是根据备选方案与理想解的接近程度进行排序,从而确定各方案相对优劣的一种方法,在实际生产中得到了较多应用。文献[1]运用TOPSIS 法对西部地区工业经济效益进行了综合评价。文献[2]运用TOPSIS 法对混煤配比方案进行了评价。
常规TOPSIS 法存在的问题之一是,其权重系数需要主观给定,导致个人主观性对评价结果产生影响。为此,有研究针对这一问题进行了改进,文献[3-5]将熵权概念引入TOPSIS 法并应用于电厂混煤配比方案的综合评价,避免了主观意识对权重的影响,取得了较好的效果。但当评价指标维数较高时,熵权法存在计算过程复杂、计算速度相对较慢、实时性较差的缺点。引入主成分分析法(PCA 法)可有效降低维数,提高计算速度。文献[6]运用PCA法将较多维数的衡阳市土地生态安全评价指标进行降维处理,取得了简化运算的效果。文献[7]针对福建省区域经济差异的评价问题,综合PCA 和TOPSIS 法给出评价结果,在此评价过程中TOPSIS法的权重仍然依靠主观设置。文献[8]利用PCA-TOPSIS 法对中国学术期刊进行了评价,所得结果与实际接近。文献[9]将主成分贡献率归一化后作为TOPSIS 法的权重,用于区域体育产业综合竞争力的评价,避免了主观意识对评价结果的影响,解决了权重选取的问题。文献[10]运用熵权TOPSIS法与单一PCA 法分别对期刊学术影响力进行评价,前者解决了权重选取问题后者则简化了计算过程。
常规TOPSIS 法存在的问题之二是,当待选方案增减时可能会造成理想解变化,导致其他方案之间相对排序发生变化,即逆序现象。针对这一问题,文献[11]提出了一种两两方案间使用TOPSIS 法的综合评价方法,但这会带来过多的计算量。文献[12-13]给出了常规TOPSIS 法产生逆序现象的原因分析且提出了加入绝对正、负理想解的改进办法,能有效解决逆序现象。
针对目前采用的PCA-TOPSIS 法仍然存在的逆序问题,本文提出了一种基于PCA 和改进TOPSIS法的混煤配比方案综合评价方法。该方法首先基于PCA 法对评价指标进行降维处理并将主成分的贡献率作为权重向量;然后采用绝对正、负理想解避免逆序现象的发生;最后,以某电厂6 种混煤方案及其12 个评价指标为算例,对该综合评价方法进行了验证[14-15]。
1 PCA 与TOPSIS 法的分析与改进
1.1 评价指标PCA 法降维处理
PCA 法是利用变量间的线性相关性,其中线性无关的变量成为主成分,并用主成分来代替原来众多的变量。混煤配比方案的评价指标经过PCA 法降维后,提取出了具有代表性的几个评价指标且可以最大程度上的保留原数据信息。PCA 法的主要计算过程[6]如下。
设某多数性决策问题有n个评价对象和p个评价指标,则xij对应第i个对象第j项指标的数值。则原始决策矩阵为
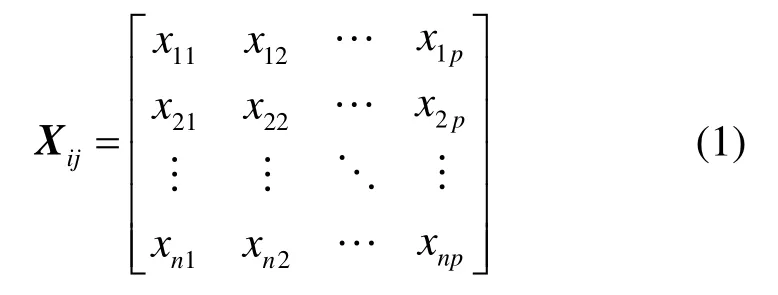
式中:i=1,2,…,n;j=1,2,…,p。
1)分析指标类型,并趋势同一化。用倒数法或差值法将成本型指标转化为效益型指标,其他正指标数据保持不变。
2)标准化原始决策矩阵y。
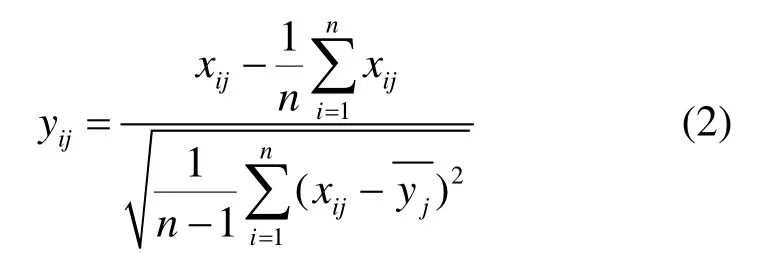
3)计算相关系数矩阵R,并计算特征值。
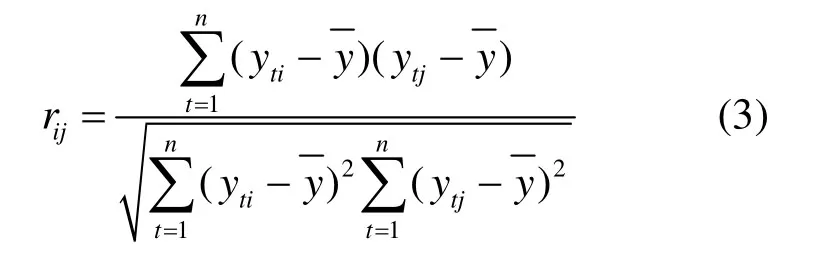
式中,rij(i,j=1,2,…,p)。为原变量yi与yj的相关系数。
4)计算特征值和特征向量。首先求出特征值(i=1,2,…,p)及其对应的特征向量ei(i=1,2,…,p),并使特征值按从大到小的顺序排列,即
5)计算各主成分贡献率及累计贡献率。一般情况下,取累计贡献率在85%到95%区间内的特征值作为主要成分,或者取特征值大于1 的作为主要成分。
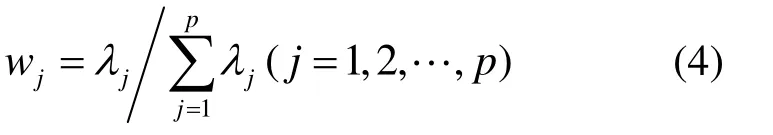
6)计算主成分荷载矩阵及其得分。
主成分荷载
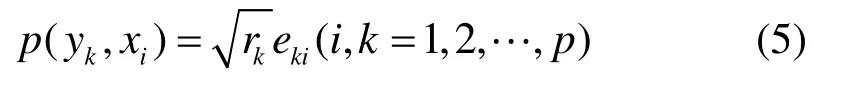
主成分得分系数矩阵F

式中,pj为主成分荷载矩阵的列向量。
1.2 常规TOPSIS 法决策过程
常规的TOPSIS 法主要涉及权重的选取、相对理想解的求取以及相对接近度的计算[2],具体决策过程如下。
1)规范决策矩阵Y可由式(1)得到。
2)人为确定权重向量w={wj},其中j=1,2,…,p。
3)构造规范决策矩阵Y={yij}和权重向量w={wj}的点积构成加权规范矩阵z={zij}。

式中:i=1,2,…,n;j=1,2,…,p。
4)由于所有成本型评价指标已经转化为效益型评价指标,所以相对正理想解h+和相对负理想解h‒为:

式中,j=1,2,…,p。
5)确定各方案分别到相对正理想解h+和相对负理想解h‒的欧氏距离d+和d‒。
6)确定各方案的相对接近度Ci。
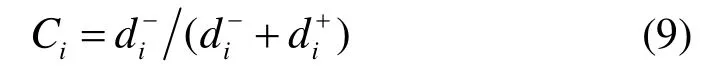
式中,i=1,2,…,n。
2 基于PCA 和改进TOPSIS 法的综合评价模型
2.1 TOPSIS 法产生逆序的原因
常规的TOPSIS 法是从综合评价矩阵中选取最大、最小值构成相对正、负理想解,而增加或减少方案,会改变各个指标的最大或最小值,进而改变正负理想解。从空间关系来看,TOPSIS 法的相对接近度是各个方案参照正、负理想解的空间位置关系,正、负理想解的改变也是空间参照标准的改变,评价结果势必会出现逆序的结果。
假设每个方案有2 个同为效益型的指标,且2 个指标对应的权值相等,即w1=w2=0.5。利用常规TOPSIS 法计算相对正、负理想解,进而计算相对接近度,得到方案的优劣排序;作为对比,现删除方案4,同样利用常规TOPSIS 法得到方案的优劣排序。4 个方案、评价指标及移除方案前后评价结果见表1。

表1 4 个方案及其评价指标Tab.1 Four schemes and their evaluation indexes
将移除方案4 前后的方案和相对正、负理想解的位置标注在坐标系中,结果如图1所示。

图1 删除最优方案对评价体系的影响Fig.1 The effect of deleting the optimal solution on the evaluation system
由图1可以看出,由于最优方案4 的缺失,方案1、3 的排名发生了颠倒,这是由于整个评价体系的环境发生了变化,即相对正、负理想解的位置出现变动所致。而在实际中,2 种方案的排名应该不受最优(劣)方案变化的影响。常规TOPSIS 法正是受这种缺陷影响,容易导致决策错误,也使得其在如今大数据及动态评价系统中更加难以应用。
2.2 基于PCA 和改进TOPSIS 法的综合评价模型
本文提出的PCA 和改进TOPSIS 法不仅保留了降维和权重设置的优势,并在此基础上解决了逆序的问题,具体计算过程如下。
1)由标准化原始决策矩阵Yn×p和主成分得分系数矩阵Fn×m可以得到主成分得分矩阵S={sij}。

2)以主成分得分矩阵S={sij}及各主成分贡献率构造综合评价矩阵,记为G={gij}。
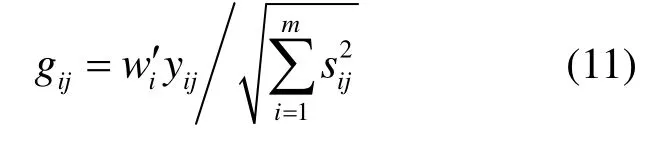
式中:i=1,2,…,m;j=1,2,…,n;第i个主成分权重为
3)改进的TOPSIS 法,分别选取绝对正理想解和绝对负理想 解:Z+=(1,1,…,1)1×m,Z‒=(0,0,…,0)1×m。
4)按照常规TOPSIS 法步骤计算,最后对比接近度大小对各混煤评价方案优劣进行排序,接近度越大,表明越接近最优水平。
3 电厂混煤配比方案评价
3.1 评价指标体系的建立
根据某煤电公司的燃料来源,为了尽量匹配锅炉的设计用煤,采用贺斯格乌拉煤(校核煤种)、沙尔塔拉煤和山西葛铺煤3 种煤进行配比,以水分、挥发分、灰分、固定碳和硫分等12 个量为性能指标。采用基于PCA 和改进TOPSIS 法对6 种混煤方案进行综合评价。设计煤种及掺烧煤种性能指标见表2。

表2 设计煤种及掺烧煤种性能指标Tab.2 The performance indexes of the designed coal and blended coal
在所有指标中,挥发分、固定碳和热值为煤炭评价指标中常见的效益型指标,其成分的增加会使得煤炭更加易燃、热量更高;而灰分和水分会影响单位重量煤炭的碳含量,影响燃烧并降低热量,且灰分会在炉膛中结焦,影响锅炉受热面,降低其效率,进而降低经济性;灰分软化温度越高,熔融状态的灰分越不易在锅炉中结焦;而随着煤炭中酸性氧化物(Al2O3)的含量大于碱性氧化物(Fe2O3),灰分软化温度越高。
考虑到评价方案与锅炉设计煤种的偏离程度,在评价体系中加入混煤方案评价指标和设计煤种的偏差:其中xij为混煤方案的评价指标,qij为设计煤种的评价指标,j=1,2,…,p。
表3为混煤配比方案及其性能指标。表中将混煤配比的12 个性能指标分为效益型指标和成本型指标,分别用+和-表示。

表3 混煤配比方案及性能指标Tab.3 The coal blending schemes and their performance indexes
3.2 计算过程
运用MATLAB 软件对6 个混煤配比方案的12 个评价指标编程进行主成分分析。由式(2)计算其相关系数矩阵,得出标准化数据。主成分矩阵及其对应权重见表4,表中每个主成分(PC1、PC2、PC3)均为12 个变换后评价指标(X1—X12)的线性组合,其中各指标权重由主成分矩阵和主成分权重计算并归一化后得出。然后,计算各指标对应的贡献率,结果如图2所示。
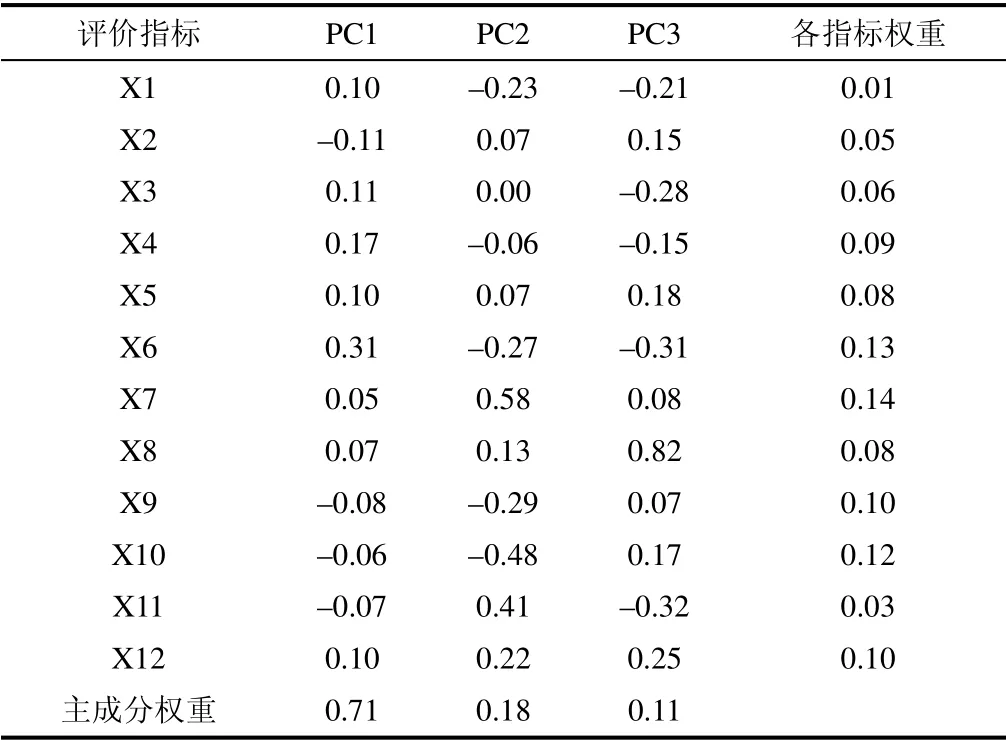
表4 主成分矩阵及其对应权重Tab.4 The component matrix and its weight

图2 各成分及其累计贡献率Fig.2 The composition and its cumulative contribution rate
从图2可以看出,运用PCA 法对混煤方案的12 个评价指标进行降维处理,得到3 个主成分的累计贡献率为98.15%。以此3 个主成分贡献率及其得分系数矩阵来构造综合评价矩阵,可以在尽量保持信息不丢失的情况下减少运算量,提高TOPSIS 法的评价效率。构造出综合评价矩阵后,计算各个方案评价指标与绝对正理想解和绝对负理想解之间的欧氏距离,以及绝对接近度,结果见表5。
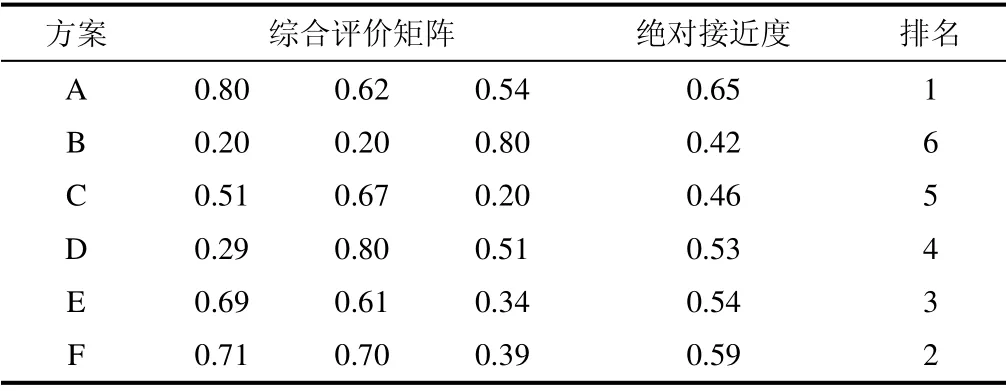
表5 综合评价矩阵Tab.5 The comprehensive evaluation matrix
3.3 评价结果合理性分析
在以上评价结果中,方案A 的各项指标均介于设计煤种和校核煤种之间,说明此方案完全可以保证锅炉的正常燃烧;由于电厂每天需要燃烧大量的煤,方案均价的降低可以带来极为可观的经济效益。综上所述,方案A 既可以保证锅炉的稳定燃烧又可以提高锅炉的经济性。
3.4 PCA 和改进TOPSIS 法抗逆序性验证
3.4.1 常规PCA-TOPSIS 法抗逆序验证
从评价体系中移除最优方案A,再利用常规PCA-TOPSIS 法进行评价,评价结果见表6。由表6可以看出:在常规PCA-TOPSIS 法移除最优方案A后,方案E 与方案F 的相对排名发生了变化,出现了逆序现象;从合理性分析,在主要评价指标和价格相差不大的情况下,较优的方案应当是更加接近设计煤种的方案F,所以逆序问题会导致评价结果出现偏差。
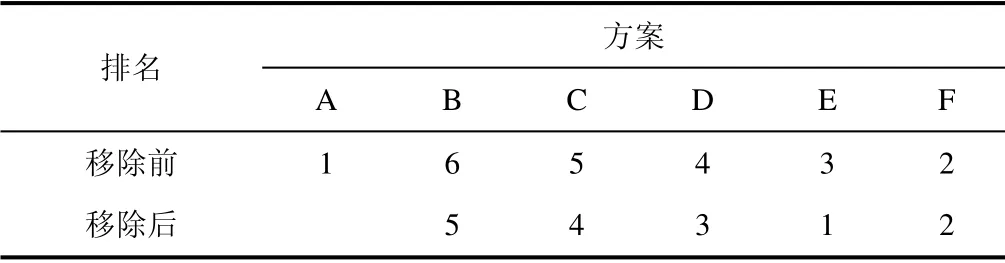
表6 常规PCA-TOPSIS 法逆序问题对比Tab.6 Comparisons of the conventional PCA-TOPSIS method in reverse order
3.4.2 PCA 和改进型TOPSIS 法抗逆序验证
对于PCA 和改进型TOPSIS 法,同样从评价体系中移除最优方案A 并记录评价结果,移除方案A前后的评价结果见表7。从表7可以看出,当最优方案A 退出评价体系后,由于引入了绝对正、负理想解的概念,使得各方案的相对排序位置不变,消除了逆序的影响。因此,在增减评价方案后,PCA和改进TOPSIS 法的抗逆序特性会使得排序结果更加严谨。

表7 PCA 和改进TOPSIS 法逆序问题对比Tab.7 Comparisons of the PCA and improved TOPSIS method in reverse order
从对比结果的合理性进行分析,方案F 的价格略高于方案A,但是热值却更接近锅炉的设计煤种,鉴于其较优的性能,方案F 仅次于方案A,被列为第二选择。
4 结 论
1)采用PCA 法提取评价指标主要成分,可以大大简化计算,提高评价效率;采用绝对理想解的改进TOPSIS 法可有效解决逆序问题。
2)将PCA 与改进的TOPSIS 法相结合,可采用主成分贡献率作为权重系数,消除主观因素对评价结果的影响。此方法不包含复杂的迭代、寻优过程,更加适合高维大数据动态样本的评价问题。
3)将该算法用于火电厂混煤配比评价,选出的优化配煤方案,可以很好地协调煤质成分、热值、价格等各项指标之间的关系,有效提高锅炉燃烧的安全性与经济性。
