基于长短期记忆网络的解码器设计及闭环脑机接口系统构建

2019-12-03潘红光米文毓

西安科技大学学报 2019年6期

潘红光，张奇，米文毓，马彪

（1.西安科技大学电气与控制工程学院，陕西西安710054；2.鄂尔多斯市神东工程设计有限公司，鄂尔多斯017000）

0 引言

脑机接口（Brain-Machine Interface，BMI）技术近年来发展异常迅速［1-2］。BMI技术能够通过采集人脑的电信号直接完成对输出设备的操控，实现功能障碍者与外界的交流，从而提供了一种改善功能障碍者生活质量的途径［3］。其在医疗领域如残疾人肢体功能恢复，生活领域如老年人生活辅助等方面应用也越来越广泛［4-5］。BMI系统主要组成部分为：解码器、编码器（本质均为数学模型）和大脑皮层神经元活动的量测。其中，解码器用于提取与任务相关的运动意图；编码器则将与运动相关的感知信息反馈到大脑。故BMI、大脑和假肢器官（如假臂）三者可构成闭环的BMI系统，如图1所示。

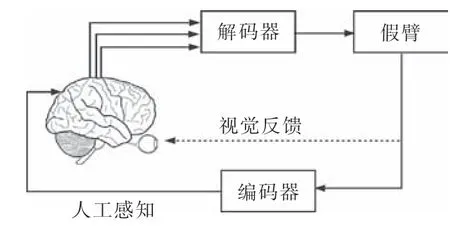
图1 脑机接口系统Fig.1 System of brain-machine interface

目前针对BMI系统解码器已有大量的研究。例如Goblu，孙京浩等人基于维纳滤波和速度衰减卡尔曼滤波设计的解码器，可以从连续的放电尖峰序列中解码出速度、位置等信息［6-7］；Shanechi等人设计一个闭环的点过程过滤解码器，可以研究反馈率和控制率对大脑控制连续BMI运动的影响（控制率表示从大脑向假体发送运动命令的频率，反馈率表示向对象提供假体的视觉反馈的频率）［8］；潘家辉等人从多方面对P300成分进行特征提取，并采用贝叶斯线性判别分析的方法进行模式分类［9］。但是在上述解码器中都未曾考虑脑电信号与时序的相关性。而脑电信号是一个动态的时间序列并且其控制的外部设备（如假肢）的运动过程也是渐变的。而长短期记忆网络（Long Short-Term Memory，LSTM）适合处理与时间序列高度相关的问题，并且在学习新信息的同时保持历史信息持久化，因此基于LSTM网络设计BMI系统解码器，以期获得更好的解码效果。

近年来，针对BMI系统的研究已取得广泛的进展，例如Wodlinger等人同时从植入受试者左侧运动皮层的2个96通道皮质内电极阵列中提取手形指令，实现被试者多自由度控制假肢［10］。Hong和Orsborn等人引入视觉反馈，证明闭环BMI系统较开环BMI系统拥有更好的可靠性以及执行效率［11-12］。Hortal和Abdullah等通过支持向量机和神经网络对脑电图（electroencephalogram，EEG）信号进行分类作为控制指令驱动外部设备［13-14］。

基于Bullock等人提出的单关节信息传输（Single-Joint Information Transmission，SJIT）模型，设计基于LSTM网络的解码器来表征放电信号与肢体运动的非线性关系，并通过SJIT模型生成大量训练和测试数据，来训练、测试解码器；此外，为了在感觉反馈通路缺失时，仍能准确地恢复肢体运动功能，在设计长短期记忆网络解码器的基础上，结合数据驱动的无模型控制（Model-Free Control，MFC）策略设计的辅助控制器构造闭环BMI系统恢复关节活动障碍者缺失的感觉反馈通路从而实现跟踪期望轨迹的目的。

1 SJIT模型简介

Bullock等提出的SJIT模型［15］，如图2所示。在模型中，GO为可变幅门信号，各神经元组分别表示如下：DVV为期望速度向量（Desired Velocity Vector，DVV），OPV为输出位置向量（Outflow Position Vector，OPV），OFPV为输出力和位置向量（Outflow Force and Position Vector，OFPV），SFV为静态力向量（Static Force Vector，SFV），IFV为惯性力向量（Inertial Force Vector，IFV），PPV为感知到的位置向量（Perceived Position Vector，PPV），DV为偏差向量（Difference Vector，DV），TPV为目标位置向量（Target Position Vector，TPV），JPV为关节位置向量（Joint Position Vector，JPV），γD动态γ神经元（dynamic gamma motoneurons），γS静态γ神经元（static gamma motoneurons），α为α神经元（alphamotoneuron），Ia为Ia型传入纤维（type Ia afferent fibers），Ⅱ为Ⅱ型传入纤维（type Ia afferent fibers）。大脑区域包括区域4和区域5.

图2 SJIT模型（“-”为抑制性反馈通路；无“-”为刺激性反馈）Fig.2 SJIT model

DV神经元组计算TPV和PPV间的偏差。DV神经元组平均放电活动（average firing activity）ri由下式描述

式中0≤ri（t）≤1，下标i对应主动肌（agonist muscle）。在后续介绍中，下标i均对应主动肌；而下标j均对应被动肌（a ntagonistic muscle）。Ti为主动肌i的TPV；xi（t）为PPV神经元组平均放电率，这些神经元可连续计算出主动肌当前位置；Br表示DV神经元组基础放电活动（base firing activity）。

通过DV神经元组连续计算偏差向量，进而通过DVV神经元组进行比例放缩后得到DVV神经元组平均放电活动ui（t）

式中Bu为DVV神经元组基础放电活动；g（t）为GO信号，并假定其来自于基底神经节（basal ganglia）。DVV神经元组的放电活动仅仅在运动过程中进行，且其平均放电活动代表了相位移动时间（phasic-movement time）。GO信号g（t）动态为

式中常量ò为慢积分率（slow integration rate）；g0为前脑决策中心的一个阶跃输入；常量C为GO信号饱和值。

OPV神经元组可接收DVV和PPV神经元组的信息，其平均放电活动表示为

式中 η为比例因子。静态运动神经元组（static motoneurons）和动态运动神经元组（dynamic motoneurons）分别由γSi（t），γDi（t）表示，其平均放电活动为

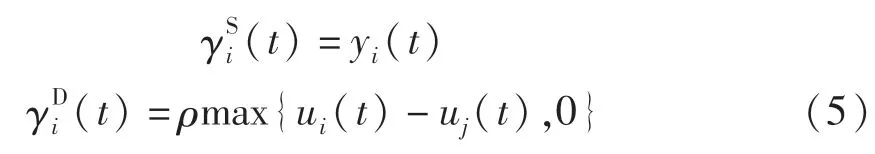
式中 ρ为放缩因子。Ia型和Ⅱ型肌肉传输纤维平均放电活动由式（6）获得

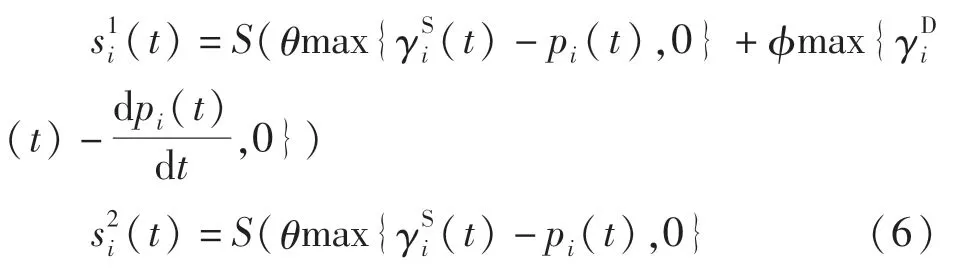
式中s1i（t）和s2i（t）分别为Ia型和Ⅱ肌肉传输纤维的平均放电活动；pi为主动肌i的位置；θ为静态核袋纤维（static nuclear bag and chain fibers）的灵敏度；φ为动态核袋纤维（dynamic nuclear bag fibers）的灵敏度。传入纤维活动饱和值可由式S（ω）=ω/（1+100ω2）给出。PPV神经元组平均放电活动xi（t）见式（7）

式中 τ为反馈延时，Θ为增益常量。IFV神经元组平均放电活动qi（t）见式（8）

式中 Λ为常数阈值。而SFV神经元组平均放电活动则由式（9）表示

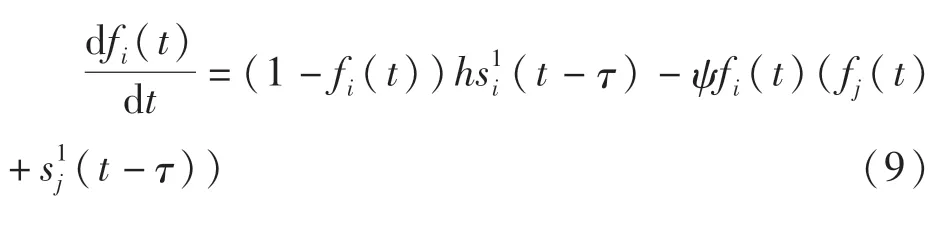
式中 ψ为抑制性放缩参数（inhibitory scaling parameter）；h为常量增益，其用来控制外部负载补偿（external load compensation）的大小和速度。OFPV神经元组平均放电活动ai（t）主要用来体现神经元组的相位补偿（phasic-tonic），其可由下式表示

α神经元组平均放电活动由式（11）表示

式中 δ为牵张反射（stretch reflex）增益。基于上述模型，臂部活动可由下式描述

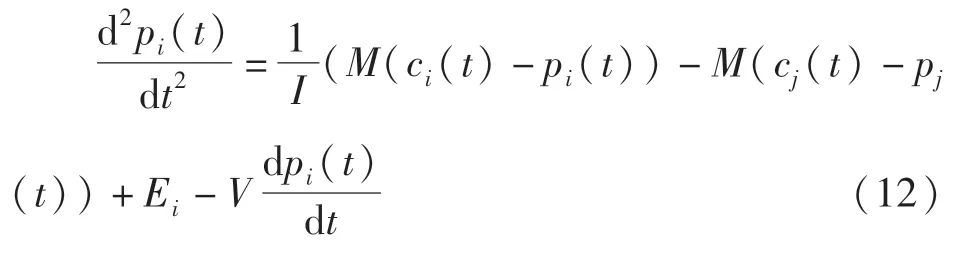
式中主动肌位置pi（t）始终位于主动肌运动的近端和远端距离（origin-to-insertion distances）之间；类似地，pj（t）则表示被动肌位置，且与主动肌位置之间满足pi（t）+pj（t）=1，此式是该模型的重要约束。Ei为施加于臂部关节的外部力。式M（ci（t），pi（t））=max｛ci（t）-pi（t），0｝为主动肌i的生成力总和。M（ci（t）-pi（t））-M（cj（t）-pj（t））记作ΔM，ci（t）表示肌肉收缩活动（contraction activity），其动态表示为

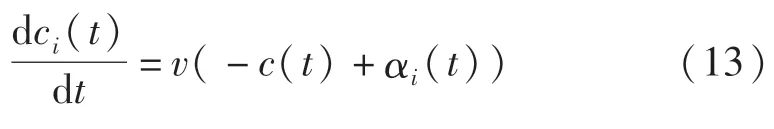
式中v表征收缩率（contraction rate）的大小。

注意：该模型中，没有考虑视觉反馈。在文中仿真中，均采用主动肌位置pi（t）为肢体位置。

2 基于LSTM网络设计的解码器

对于健康的人而言，本身拥有一个完整的信息回路，如图2所示，大脑区域4的DVV，OPV及OFPV神经元组通过脊椎电路来传递肢体运动的指令，由感觉反馈部分进行反馈。然而对于关节活动障碍者而言，脊椎电路通路缺失，无法完成上述信息流闭环。因此则需要解码器来恢复脊椎电路通路，即用解码器来代替原有脊椎电路通路将大脑信号传递给假肢［16-18］。

2.1 解码器设计

图3 LSTM单元Fig.3 LSTM unit

LSTM网络由Hochreiter S和Schmidhuber J在1997年提出，是为解决循环神经网络（Recurrent Neural Networks，RNN）“长距离依赖”问题的一种改进算法［19-20］。LSTM的细胞单元结构如图3所示。

LSTM的细胞单元在RNN的基础上加入了有3个门，分别是输入门（Input Gate），遗忘门（Forget Gate），输出门（Output Gate）。输入门用来控制信息输入，决定有多少将添加到记忆信息中；遗忘门用来控制细胞历史状态信息的保留，激活函数σf使得遗忘门的输出值在［0，1］之间，当遗忘门输出接近0时的时候，表示将上一状态的信息丢弃越多，接近1的时候，表示上一状态的信息保留越多；输出门用来控制信息输出，决定多少记忆信息被用于下一阶段的更新中。

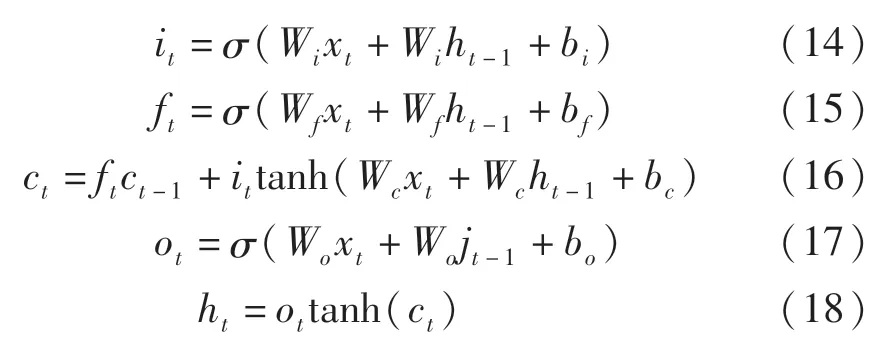
上述过程可用以上公式表示，xt为输入；ht为输出；it为输入门的输出；ft为遗忘门的输出；ct为当前时刻t的细胞单元状态；ot为输出门的输出，其中W和b为参数矩阵和偏置矩阵。

基于LSTM网络设计解码器来表征放电信号与肢体运动的非线性关系，选取DVV，OPV，OFPV神经元组的放电活动作为输入，选取主动肌与对抗肌的合力差ΔM作为LSTM网络的输出。

在输入层，使输入特征向量形式为x（t）=［x1（t），x2（t），x3（t），x4（t），x5（t），x6（t）］T并选取相对应的放电活动为：x1（t）=ai，x2（t）=aj，x3（t）=ui，x4（t）=uj，x5（t）=yi，x6（t）=yj.在输出层，选取合力差作为输出变量ht=ΔM，其中的隐层单元维数选取50，学习率选取为0.01.

2.2 数据生成及其离线测试

基于LSTM网络设计的解码器，其中的参数需要大量的数据训练来得到，所以此处利用SJIT模型生成大量的训练数据以及测试数据，如图2所示，利用式（1）～（13）来构建模型生成大脑皮层神经元放电平均放电率、主动肌与对抗肌的合力差、臂部的速度、位置以及关节转矩等数据。生成的训练数据是对臂部关节的伸展任务进行了共计1 600次模拟仿真，在每次臂部关节的伸展时，以采样时间0.01 s对大脑区域4各神经元组（DVV，OPV及OFPV）、主动肌神经元组以及被动肌神经元组的平均放电活动进行采样，主动肌与对抗肌的合力差ΔM（t）=M（ci（t），pi（t））-M（cj（t），pj（t））也被采样记录。因为每次模拟臂部关节的伸展耗时约为3s，所以经过上述1 600次的模拟，可以得到共计480 000组的数据。文中，选取前470 000组数据进行训练，后10 000组数据进行测试。以下为具体变量和参数的设置：xi（0）=xj（0）=0.5，yi（0）=yj（0）=0.5，pi（0）=pj（0）=0.5，ui（0）=uj（0）=Bu，ri（0）=rj（0）=Br之外，其他变量的初始条件均设定为0.I=200，V=10，v=0.15，Br=0.1，Bu=0.01，Θ=0.5，θ=0.5，φ=1，η=0.7，ρ=0.04，λi=150，λj=10，Λ=0.001，δ=0.1，C=25，ò=0.05，ψ=4，h=0.01，τ=0.参数g0通过均值为0.75，方差为0.002 5的高斯分布随机生成，生成后，其作为一组常数在仿真中存在。

图4 解码器离线测试Fig.4 Offline performance comparison

选取10 000组测试数据中［2 000，3 000］组的数据展示仿真结果，离线测试结果如图4所示，由于测试数据通过采样得到，是离散化数据，所以采用ΔM（k）表示，其中实红线表示实际的ΔM（k），蓝点画线表示离线解码的ΔM（k），并引入均方根误差评价指标（RMSE），作为解码器的评价指标。

式中 Δ¯M（k）为实际数据，即SJIT模型的采集的合力差，ΔM（k）为解码数据。LSTM网络设计的解码器的均方根误差值为4.3×10-2，表明LSTM网络设计的解码器良好的解码效果。

3 闭环BMI系统构建

感觉反馈通路缺失时，仅仅通过基于LSTM网络设计解码器难以准确恢复肢体运动功能［15-17，22-23］。所以通过设计解码器以及MFC辅助控制器，构造闭环BMI系统跟踪期望轨迹达到恢复肢体运动功能的目的。其中，期望轨迹为基于SJIT模型在加入解码器情况下跟踪目标所产生的神经元组PPV的平均放电率xi（t），如图5所示。注意，文中人工反馈设计中没有补偿IFV和SFV神经元组的反馈信息。

图5 闭环脑机接口系统Fig.5 Closed-loop brain-machine interface system

3.1 辅助控制器设计

无模型控制（MFC）是一种只依赖于系统的输入输出数据，不依赖于被控系统模型的自适应控制方法，并且不需要复杂的人工控制器参数整定［24-25］。选取控制输入准则函数如下

式中 φ（t）为被控系统的伪偏导数，它是一个时变参数；I（t）为被控系统输入，即控制器输出；ΔI（t）为I（t）的增量；λ为权重系数。在准则函数中引入惩罚来限制输入的变化。在脑机接口系统中，由于人类本体反馈的缺失，si和sj均等于0.

将公式（21）代入（20）中，对I（t）求导，并令其为0，可得

参数ρt的引入可加强公式（22）的通用性。参数λ的引入可避免出现分母为0的现象。由于伪偏导数φ（t）未知，不能直接用于式（22）可以利用相似的方法求出伪偏导的估计值

式中 ηt和μ与公式中的参数ρt和λ功能类似；即为求得的伪偏导数的估计值。将代入公式（22），便可得到控制器的输出I（t）.根据设计好的脑机接口系统框架，用求得的I（t）代替单关节活动信息传输电路模型公式（7-τ），即用公式（25）替换公式（7）。

4 仿真结果

首先为验证MFC辅助控制器的跟随效果：基于上述闭环BMI系统框架，采用python进行仿真实验，闭环BMI系统框架的各参数选取与2.2节参数相同。采样时间选取0.01 s，g0=0.75，Ti（t）选取：初始位置为0.7，初始速度为-0.1/s，并以此速度移动1 s后保持不变，MFC辅助控制器的相关参数选取ηt=1，μ=1，ρt=7，λ=2，^φ（0）=-2得到闭环BMI系统下PPV神经元组的平均放电率跟踪效果，如图6所示，其中红实线表示期望轨迹xi（t），蓝点画线表示MFC辅助控制器作用下的跟随轨迹xi（t）.计算图6中跟随轨迹xi（t）的均方根误差值RMSE以及相对误差，均方根误差为5.9×10-4，相对误差如图7所示，其最大值不超过1.2%.证明MFC辅助控制器的跟踪效果良好。

图6 PPV平均放电率对比Fig.6 Comparison of the average firing rate of PPV

图7 PPV平均放电率相对误差Fig.7 Relative error of average firing rate of PPV

验证构建的闭环BMI系统有效性：采用构建的闭环BMI系统与SJIT模型进行比较。各参数选取同上。仿真结果如图8所示，红实线为SJIT模型的输出轨迹，蓝点画线为文中构建的闭环BMI系统的输出轨迹，图9为恢复轨迹的相对误差。由仿真结果可知，恢复轨迹的相对误差最大值不超过3%，说明文中设计闭环BMI系统恢复了手臂的运动功能，证明构建的闭环BMI系统的有效性。