信息论安全的3个基础外包计算协议及空间位置关系保密判定

陈振华，黄路琪，史晓楠，聂靖靖

（1.西安科技大学 计算机科学与技术学院，陕西 西安710054；

2.桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林541004）

0 引 言

安全多方计算最早由Yao提出，是指各个参与方在不泄露各自输入隐私的情况下，能正确合作计算出某个问题。保护隐私的合作计算都可归为安全多方计算［1］，例如，保护隐私的数据挖掘［2-4］，统 计 计 算［5-7］，机 器 学 习［8-10］，数 据 聚合［11-14］，外包计算［15-17］，和数据查询［18-19］等。

安全几何计算是安全多方计算的一个重要分支，是指各参与方在保护各自数据隐私的情况下，共同计算一个几何问题。例如：投资公司A，B想要扩展市场，A想知道自己的投资范围是否在B的范围内，但B的计划是商业机密，而A也不想告诉B自己的投资计划，在不暴露各自商业机密的前提下，双方如何解决这个问题？

若将公司的投资计划看成平面区域，对应的数学模型是：保密判定空间中2个平面是否相交。而要判定此关系，需要先解决向量安全计算问题。外包计算是目前流行的一种计算模式，但服务器作为不可信第三方，可能会泄露用户隐私。因此，在利用外包服务的同时，如何保护各参与方数据隐私解决向量计算问题并进一步解决平面判定问题，成为目前一个较新的研究方向。

针对向量安全计算，以往的学者提出了一些解决方案。周素芳等人利用哥德尔编码和同态加密解决了向量线性组合计算问题，该方案使用了公钥加密，不是信息论安全，也不适用于外包计算［20］。陈振华等人提出了基于同态加密的向量内积外包计算协议。该协议适用于外包计算，但不是信息论安全且复杂度较高［21］。张卫国等人引入不可逆矩阵来保护数据隐私，计算了向量内积［22］，Li等人借助内积运算来判定空间位置关系［23］。虽然协议都达到了信息论安全，但并不适用于外包计算。

针对以上方案的不足，文中利用矩阵论中一些特殊函数的性质和随机数混淆的方法来保护数据隐私，并利用外包计算节省成本。在此基础上，设计了安全外包计算的向量内积、向量模长和向量夹角计算协议，并解决了空间面与面的保密位置判定问题。

1 模型简介

1.1 半诚实模型

安全多方计算的协议运行环境分为半诚实参与者模型和恶意参与者模型［24-29］。文中协议都建立在半诚实模型下，因此这里只给出半诚实模型定义。半诚实参与者是指协议方诚实地执行协议，不会篡改输入和输出信息，但可能会保留计算的中间结果，试图从中间结果和最后输出推导出协议之外的信息或者他人的信息。

1.2 半诚实模型下的安全性定义

外包计算中半诚实模型下的安全两方计算的模拟范例定义如下：设Alice拥有x，Bob拥有y，Server是外包服务器，f（x，y）为概率多项式函数；π是计算f的协议。Alice，Bob和Server要在不泄露x，y给任何一方的前提下，合作计算函数f（x，y）=（f1（x，y），f2（x，y））。

Alice（Bob）执行协议π时得到的视图为viewπ1（x，y）（viewπ2（x，y））；viewπ3（x，y）为Server的视图；viewπ4（x，y）（viewπ5（x，y））为Server和Alice（Bob）合谋的视图。其中E（x），E（y）分别表示Alice和Bob发送给Server的数据，即Server获得的输入。

定义1 在外包计算环境下，如果存在概率多项式的模拟器S1，S2，S3，S4，S5使得表1中的5个式子同时成立，则称协议π保密地计算了f.

表1 外包计算中安全两方计算的安全性Table 1 Security of secure two-party computation in outsourced computation

1.3 特殊函数

1.3.1 正交变换

正交变换是指在欧式空间V中的线性变换f，若存在x，y∈V，满足＜fx，fy＞=＜x，y＞，则称f为正交变换。

1.3.2 单向函数

如果函数f：｛0，1｝*→｛0，1｝*满足下列2个条件，则称f为单向函数。

1）存在一个确定的多项式算法A，能够接受输入x，输出函数值f（x），即A（x）=f（x）；

2）对任意概率多项式时间算法A′，任意的正多项式P（.）以及充分大的n都有

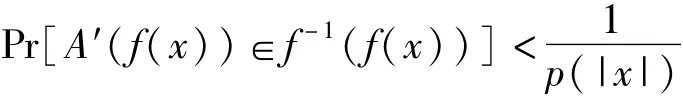
2 安全外包向量计算协议

协议1 保密计算向量内积

输入：Alice保密输入向量X=（x1，x2，…，xn），Bob保密输入向量Y=（y1，y2，…，yn），且n≥2.

输出：Alice和Bob都能知道向量X和Y的内积，但外包服务器不知道结果。

1）Alice和Bob分别选择随机数r1和r2，和具有正交性的单向函数f.Alice计算r1fX发送给外包服务器。

2）Bob计算r2fY发送给外包服务器。

3）云服务器收到Alice和Bob发来的数据，计算r1fX和r2fY的内积，得到结果r1r2＜X，Y＞，即＜r1fX，r2fY＞=r1r2＜X，Y＞，并将结果传递给Alice.

协议2 保密计算向量的长度

输入：Alice保密输入向量X=（x1，x2，…，xn），且n≥2.

输出：Alice得到向量X的长度，而外包服务器不知道结果。

1）Alice选取随机数r和具有正交性的单向函数f，计算并传给外包服务器。

2）外包服务器计算rfX和rfX的内积，得到r2＜X，X＞，即＜rfX，rfX＞=r2＜X，X＞，并将结果传给Alice.

协议3 保密计算向量夹角

输入：Alice保密输入向量X=（x1，x2，…，xn），Bob保密输入向量Y=（y1，y2，…，yn），且n≥2.

输出：Alice和Bob都能得到2个向量的夹角，但外包服务器不知道结果。

Alice和Bob分别调用协议2，保密计算向量X和Y的模长。

1）Alice和Bob分别选择随机数r1和r2，和具有正交性的单向函数f，计算并传给外包服务器。

分析：在协议1中，Alice和Bob利用函数f的正交性，将对向量X和Y的内积计算转换成fX和fY的内积计算。又利用f的单向性对向量X和Y保护隐私，得到fX和fX，由于f具有单向性，因此任何人都不能得到初始输入X和Y.又因为随机数的加入，所以数据r1fX，数据r2fY和随机数具有了不可区分性，因此保护了X和Y的隐私。此外，Alice和Bob利用随机数r1和r2混淆了fX和fY内积结果，由于结果中含有Alice和Bob的随机数乘积r1r2，因此外包服务器无法获得真正的内积值。即使考虑合谋，由于Alice和Bob不可能合谋，因此外包服务器无法同时获得两方的随机数r1和r2，从而无法获得合谋条件下内积结果。即协议1保密地计算了向量的内积。

类似的方法可以分析协议2和协议3，得到类似结论。

3 安全性证明

在本节，应用2.2节的模拟范例我们给出以上3个协议的安全性证明，先证明协议1.

定理1 协议1保密地外包计算了2个向量X和Y的内积。

证明 按照2.2节外包计算中半诚实模型下安全两方计算安全性的定义，需要构造表1中的5个模拟器S1，S2，S3，S4和S5.由于文章篇幅有限，因此安全性证明只给出了模拟器S1的详细过程，其他模拟器可按同样的道理得到。

在协议1中f1（x，y）=＜X，Y＞.S1将X，f1（x，y）作为输入进行模拟，并按照以下步骤执行

第1步S1选取随机向量Y′，f1（X，Y）=f1（X，Y′），即＜X，Y＞=＜X，Y′＞，然后用X和Y′进行模拟。根据协议1，将向量X转换，得到r1fX，记作X1.S1选择任意随机数r2′，将向量Y′转换，得到r2′fY′，记作Y1′.

第2步S1将r1fX和r2′fY′传给外包服务器，服务器计算r1fX和r2′fY′的内积，即，得到r1r2′＜X，Y′＞，记作C′.

此过程证明，Alice的视图只能从自己的输入和输出中得到；同理，Bob的视图只能从自己的输入和输出中得到，即Alice和Bob所获得的视图中都不包含对方的任何信息。因此证明了整个外包计算过程中，Alice和Bob都得不到对方的隐私。

通过构造模拟器S3，可得到

此过程证明，Server的视图只能从自己的输入E（X），E（Y）和输出E（X，Y）得到，即Server的视图中不包含Alice和Bob的任何信息。因此证明了整个外包计算过程中，Server都得不到Alice和Bob的隐私。

通过构造模拟器S4和S5，得到：

以上过程证明了Alice和Server合谋的视图只能从自身输入X，E（X），E（Y）和所获得的输出f1（X，Y），E（X，Y）中得到，并没有包含Bob的信息。同理，Bob和Server合谋的视图也只能从自身的输入和输出中得到，并没有包含Alice的信息。因此证明了在外包计算过程中，即使Server与其中任何一方参与者合谋，也得不到另一方的信息。

证毕。

类似的方法可证明协议2和协议3的安全性，得到以下定理。

定理2 协议2保密地外包计算了向量长度。

定理3 协议3保密地外包计算了向量夹角。

4 效率分析与比较

本节给出在外包计算的模式下，保密判断空间面与面位置关系的协议及其效率分析比较。

协议4 保密判断空间面与面的位置关系

2）Alice和Bob调用第3节中的协议3，求得2个方向向量的夹角，若cosθ≠±1，则平面∥1和平面∥2相交；若cosθ=0，则平面∥1和平面∥2垂直；若cosθ=±1，则平面∥1和平面∥2平行或重合，接着进行下一步。

3）Alice在平面∥1上任取一点，得到向量X=（x0，y0，z0，1）.Bob得到向量Y=（A2，B2，C2，D2）.Alice和Bob调用第3节中的协议1，可计算出向量X与向量Y的内积。如果内积值为零，平面和平面重合，否则平行。

由于协议4是依靠文中的协议1，协议3设计的，而第3节的安全性证明已经证明了协议1，协议3都是安全的，因此可以得到协议4也是安全的，这里不再详细证明。

由于文中和文献［21-23］都处理了空间面面位置关系问题，而文献［20］并没有处理该问题。因此就文献［21-23］处理的共同的面面位置保密判定协议做出比较和分析。为了方便比较，将模幂运算记为Me，模乘运算记为MN，乘法运算记为M，向量维数记为n，统一使用文献［21］的模数N.整个协议执行过程中，计算开销比较大的是模幂运算，模乘运算，乘法运算，因此把这些运算总个数作为衡量计算复杂度的指标，其他忽略不计。

4.1 理论分析与比较

4.1.1 计算复杂度

文献［21］的面面位置关系保密判定（协议6），整个协议计算过程中调用了2次内积协议，用户加解密过程中使用了模幂和模乘运算，其运算总个数为2MN+18Me.

文献［22］的安全计算面与面的位置关系（协议5），整个协议计算过程中调用了4次内积协议，每调用一次内积协议，用户进行2次矩阵相乘，需16次乘法，因此运算总个数为64M.

文献［23］的保密判定面与面的位置关系协议（协议4），整个协议计算过程没有调用内积协议，而是进行了3个3阶矩阵行列式运算，和3个3维向量内积运算，即9个乘法运算，因此运算总个数为36M.

文中面面位置关系保密判定（协议4），整个协议计算过程需要调用1次保密计算夹角和1次保密计算内积协议，用户运算总个数8MN+6M.

4.1.2 通信复杂度

衡量通信复杂度的指标用协议交换信息的比特数，或者用通信轮数，在多方保密计算研究中通常使用轮数。

文献［21］的面面位置关系保密判定（协议6），整个协议计算过程中调用了2次保密计算内积协议和1次比较协议，内积协议每调用一次需要3轮交互，比较协议需要2次交互。则用户和外包服务器总共进行了8轮交互。

文献［22］的安全计算面与面的位置关系（协议5），整个协议计算过程中调用了4次内积协议，内积协议每调用一次需要2轮交互，用户之间总共进行了8轮交互。

文献［23］的保密判定面与面的位置关系协议（协议4），整个协议计算过程中没有调用内积协议，用户之间总共进行了2轮交互。

文中面面位置关系保密判定（协议4），整个协议计算过程调用了1次保密计算夹角协议和1次保密计算内积协议，分别需要进行5轮和3轮交互。则用户和外包服务器之间的总轮数为8轮。

4.1.3 性能

以各个协议取得的安全性级别，是否适用于外包计算和能够解决的空间位置问题作为衡量性能的标准。以“√”代表协议能够解决的空间位置问题。

综合以上，得到文中协议4和文献［21-23］的效率比较见表2，性能比较见表3.

由文献［30］可知，1个模幂运算等价于logN个模乘运算。假设这里所有协议都采用和文献［30］同样的操作平台，可将表2中文献［21］方案的计算个数换算为2MN+36logNM.因此由表2可以看到，相比于文中协议4，以往的方案［21-23］计算开销较大。由于文中利用矩阵论中一些特殊函数的性质保护数据，并没有使用公钥加密的方法，因此计算复杂度和通信复杂度较低，更具有实践意义。从表3可以看出，方案相比以往的方案，不仅实现了信息论安全，也适合外包计算，并且所能处理的空间位置关系也更加广泛。

表2 文中方案与现有方案的效率比较Table 2 Efficiency comparison of proposed approach and existing approaches

表3 文中方案与现有方案的性能比较Table 3 Performance comparison of proposed approach and existing approaches

4.1.4 传统模式和外包模式下计算成本比较

由于保密内积计算是整个安全外包计算的核心基础，为了方便其他复杂安全多方计算问题架构于此，因此文中协议1提供了外包模式下简洁的保密内积计算方案。这里仍采用和上文相同的标记符号，计算复杂度记为O，得到协议1在传统模式（非外包）下的计算成本为3MN+M，计算复杂度为O（1）；外包模式下计算成本为2MN+（n+1）M，计算复杂度为O（n），得到协议1在2种计算模式下的计算复杂性对比如图1所示。

图1 协议1在传统模式和外包模式下的计算复杂度对比Fig.1 Computation complexity comparison of protocol 1 in traditional model and outsourced model

从图1可以看出，未借助外包计算的内积协议（曲线1）不仅用户计算成本较大，且计算复杂度随着向量维数的增大呈线性增长，因此为了节省用户的计算成本，以按需付费的方式将保密内积计算外包出去。由于该部分的计算量已经由外包服务器计算，因此不再包含在用户计算成本之内，那么架构于此基础协议（即文中协议1）的协议4也不需要保密计算内积，这样就极大地节省了用户的计算成本。

4.2 仿真实验

为了直观呈现以上协议的理论效率分析结果，在Java语言环境下将表2的4个协议编程实现。采用的计算机运行环境如下：操作系统为Windows 7旗舰版，CPU为Intel i5-5200U 2.20 GHz，内存为4.00 GB.文中协议4和文献［21］协议6主要运算为模运算，而文献［22］协议5和［23］协议4的主要运算为乘法运算。因此分为2种情况进行分析比较，第一种是将文中协议4和文献［21］协议6进行效率比较（不同模数下的耗时）；第二种是将文中协议4和文献［22］协议5，文献［23］协议4进行效率比较（判断不同位置关系的耗时）。

1）将文中协议4和文献［21］协议6在不同模式下进行耗时比较。在实验中分别取不同的模数N为143，437，899，1 517 bits，得到2个协议的平均耗时，如图2所示。

2）将文中协议4和文献［22］协议5，文献［23］协议4判断不同位置关系进行耗时比较，分别得到3个协议平行、相交、垂直、重合情况下的平均耗时，见表4.

从图2和表4可以看出，文中协议4的平均耗时低于文献［21］协议6，文献［22］协议5和文献［23］协议4的平均耗时。此外，从表4还可以看出文中协议4能判断的面面位置关系更多（文献［22］协议5不能判断面面重和，文献［23］协议4既不能判断面面重和，也不能判断面面垂直）。

综合以上实验结果，得到如下结论：无论理论分析还是实验分析，本文协议效率较高，而且能判断的空间位置关系更加广泛。

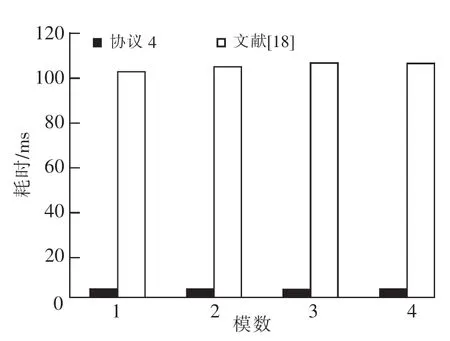
图2 文中方案与文献［21］协议6在不同模数下的平均耗时比较Fig.2 Average time cost comparison of proposed approach and protocol 6 in reference［21］under different modulus

表4 文中方案与文献［22］协议5，［23］协议4判断不同位置关系的的平均耗时比较Table 4 Average time cost comparison of proposed approach and protocol 5 in reference［22］、protocol 4 in reference［23］under different determinations

5 结 论

1）利用矩阵论中一些特殊函数的性质和随机数混淆方法在外包计算下设计了3个基础的信息论安全向量计算协议，分别是安全外包计算的向量内积，向量模长和向量夹角计算协议。

2）利用这些基础协议解决了空间面与面位置关系保密判断问题，可进一步解决金融投资等实际问题。

3）将提出的保密判定面与面的位置关系协议与其他已有方案进行了理论分析和仿真实验比较。结果显示文中提出的方案效率更高，可判断的空间位置关系更加广泛。