基于SMT方法的测试性验证试验方案设计

(海军航空大学，山东 烟台 264001)

测试性是需要在装备设计中予以考虑并实现的一种设计特性，旨在及时准确地确定装备的运行状态，同时实现对装备故障进行有效隔离的目的[1]。随着测试性技术的快速发展，对测试性水平进行评估的测试性验证试验成为了当前测试性工程领域中亟需解决的问题。测试性验证的实施旨在通过试验的方式检验和衡量装备是否满足规定的测试性指标要求，以此来指导装备测试性水平的提升[2]。

现阶段，国内外指导测试性验证试验方案多采用故障注入的方式[3-4]，即在装备中注入确定的故障样本量，然后用规定的方法对故障进行检测/隔离判定，用以得到满足指标要求值所允许的合格判定数。可见，故障注入的首要环节就是故障样本量的确定，而故障注入试验的危害性使得所有故障样本的注入无法进行[5]，所以如何科学合理有效地确定故障样本量，以及使确定的故障样本量尽可能小是研究的重难点。而方案设计的方法多为国军标准[6-7]，同时相关研究者也针对如何有效降低故障样本量的方法进行了一些研究[8-10]。针对经典测试性验证方案，文献[11]以故障检测率(FDR)为验证指标，基于研制阶段试验数据和专家经验数据运用Bayes方法确定测试性验证试验的样本量，较之经典验证方案而言，样本量得到了一定程度的降低。文献[12]利用信息熵度量验前信息，将验前信息等效为成败型数据，并以某型雷达发射分机为例验证了该方案能有效降低试验所需样本量。文献[13]运用证据理论的方法，建立了基于融合不同种类研制信息的测试性验证试验方案，结果表明测试性验证所需样本量较之经典验证方案降低，随着研制信息量的增加，所确定的故障样本量保持减少的趋势。但上述文献对于验前信息的依赖较大，当验前信息不充足时所确定的故障样本量仍然较大，不利于导弹等高精度武器装备的测试性验证试验的实施。针对SPRT测试性验证方案，文献[14]以某型导弹飞行控制系统为研究对象，提出一种基于SPRT方法的测试性验证试验方案，所确定的故障样本量较之经典验证方法有明显降低。文献[15]以二项分布模型为基础，基于Bayes方法和SPRT方法设计并制定了测试性验证试验方案，结果表明新方案所确定的平均样本量优于SPRT方法。但上述文献在试验确定前无法控制抽样样本量，虽然采取了一定的截尾措施，但是所确定的样本量仍存在较大的问题，不利于导弹等武器装备的实际验证试验。

为此，结合SPRT方法的优点，以承制方和使用方指标值构建检验问题，在此基础上确定检验点个数以及检验点取值和最大样本量的优化约束问题，同时考虑最大样本量仍较大情况下的优化截尾问题，实现基于SMT方法的测试性验证方案的设计。

1 问题描述

1.1 经典测试性验证方案

经典测试性验证方法以二项分布模型为基础，采用单次抽样方法，通常可以采用抽样特性函数进行描述[16]：

(1)

式中,p为测试性指标;(N,C)为需要确定的故障样本量以及合格判定数;F为验证试验时未能成功检测/隔离故障的次数。

当给定承制方风险值α和使用方风险值β时，(N,C)的求解需满足以下不等式约束条件：

(2)

式中,p0为承制方指标要求;p1为使用方指标要求。

研究表明，给定指标参数(p0,p1,α,β)后，通过式(2)的约束能在验证试验开展前确定试验所需样本量，但所确定的样本量过大，不利于导弹武器装备的测试性验证试验。

1.2 SPRT测试性验证方案

考虑假设检验问题：

H0:p=p0,H1:p=p1

(3)

每次故障注入试验后，以n表示当前试验的总次数，以c表示n次验证试验中累积验证失败的次数，则可以得到两种假设似然函数比为

(4)

根据双方风险α和β，即可确定似然函数比的上下阈值，通过判定λn和阈值的关系，即可对导弹装备做出相应的接受/拒收判决。

SPRT测试性验证方案在验证试验开展前不能给出试验所需的样本量，只能通过验证试验动态决定，通常采用平均样本量作为其度量指标。Wald[17]给出了SPRT方法的近似平均抽样次数，并证明了相同的指标约束条件下，SPRT方法所需的平均抽样次数要小于经典测试性验证方案所确定的固定样本量。

研究表明，SPRT方法下样本量是一个随机变量，由于样本量的随机性，会导致试验开展过程中存在最大样本量无法控制的情况，进而导致验证试验无法继续开展。

2 SMT测试性验证试验方案

针对经典测试性验证方案所确定的故障样本量过大以及SPRT方法无法预先控制试验样本量的问题，同时结合SPRT平均抽样次数优于经典测试性验证方法的优点，设计一种基于SMT方法的测试性验证试验方案，旨在保证平均样本量较小的基础上，试验最大样本量可控且能达到最小值。

2.1 插入点数量确定

SMT测试性验证试验方案是在SPRT方法的基础上，通过插入m-1个检验点对假设检验问题进行拆分，转化为m个假设检验问题：

(5)

每个假设问题均可以看成是一个SPRT验证方案，故均能得到一组平行线作为判决边界，由于各假设检验问题判决边界的斜率与检验点相关，所以通过m组平行线的交互即可确定试验最大样本量，同时能得到判决边界。在式(5)基础上首先考虑插入2个检验点的情形，则有：

(6)

显然对于检验问题(5)，由第1组假设检验对H01及H11可以确定拒绝p=p0的判决边界，并且判决边界由检验点p0、p2以及双方风险值α、β共同确定；由第m组假设检验对H0m及H1m可以确定接受p=p1的判决边界，并且判决边界由检验点pm、p1以及双方风险值α、β共同确定。而通过假设检验问题能得到同样的接受/拒收判决边界，可见插入m-1个检验点和插入2个检验点具备相同的判决边界。

假设检验问题(5)和问题(6)不同之处在于其余的m-2个插入点会对SMT方法所确定的最大样本量的值产生影响，但同时增加插入点会增加计算的复杂度。由于在确定最大样本量后仍会对截尾策略进行研究，本文考虑假设检验问题(6)中p2=pm的情形，即实施SMT测试性验证方案的实际插入点为1个。

2.2 最大样本量确定

基于2.1节插入点数量确定原则，假设检验问题可以表示为

(7)

对假设检验问题进行如式(4)所示的序贯概率比检验，则可以得到如下所示的4条直线：

(8)

式中,s1、s2为接收/拒收线的斜率;h1、h2为截距，具体可通过式(9)求解。

(9)

式中，参数A和B由承制方风险和生产方风险决定，具体如下：

(10)

基于此，可以确定如图1所示的序贯网图。

图1 序贯网图检验

(11)

式中，c0为最大样本量n0对应的合格判定数。

此外，图1根据2.1节描述的由式(8)中的4条直线对检验空间进行了划分。

① 判决边界：针对假设检验问题(7)，直线l1′为拒绝假设p=p0的判决边界，直线l2为拒绝假设p=p1(接受假设p=p0)的判决边界；

② 拒绝p=p0区、继续验证区以及接受p=p0区具体如图1所示。

由于平均样本量和最大样本量均为设计SMT测试性验证试验方案时需考虑的因素，在平均样本量小的情况下，仍需保证最大样本量较小，式(11)间接建立了检验点p2和最大样本量n0之间的关系，故考虑如下优化问题：

(12)

通过优化问题(12)即可确定最大样本量n0的最小值，以及此时检验点p2的取值。

3 截尾策略

(nt,ct)的确定原则是在满足承制方和使用方风险的前提下使得nt和ct最小，可通过两组优化问题进行求解。

① 确定截尾样本量nt。截尾样本量nt可由以下优化问题进行确定：

图2 截尾序贯网图检验

(13)

式中，αr和βr为实际的双方风险，可通过式(14)确定。

(14)

式中，Nr/Na为确定序贯网图后所有拒收/接收点的数量；ri/rj为到达当前拒收/接受点的验证失败数；ni、nj为到达当前拒收点以及接受点的总验证次数；Si、Sj为到达当前拒收/接受点的所有序贯试验序列的可能情况。

② 确定合格判定数ct。ct的确定在截尾样本量nt确定的基础上，通过以下优化问题决定：

(15)

根据上述确定的nt和ct，即可最终设计出形如图2所示的截尾SMT测试性验证试验方案。

4 案例验证

4.1 基于SMT方法的验证方案设计

某装备测试性设计指标约束参数为

(p0,p1,α,β)=(0.96,0.88,0.1,0.1)

(16)

① 依据优化问题可以得到插入点p2以及对应的最大样本量n0的变化关系曲线，如图3所示。优化问题的解即为图中标记的极小值点，可以得到p2=0.9266，对应的最大样本量的最小值为n0=⎣187.1941」=187(符号⎣」表示向下取整)。

② 在确定p2后，可以依据式(9)求得序贯网图4条直线的相关参数，s1=0.0551，s2=0.0950，h1=3.4209，h2=4.0440。

图3 n0和p2变化关系曲线

③ 由于所确定的最大样本量仍然较大，对优化问题采用搜索的方法进行求解，得到截尾样本量nt=85，在此基础上对优化问题(15)进行搜索求解，得到满足条件的合格判定数为ct=6，则可以绘制图4所示的某型装备测试性验证截尾序贯网图。

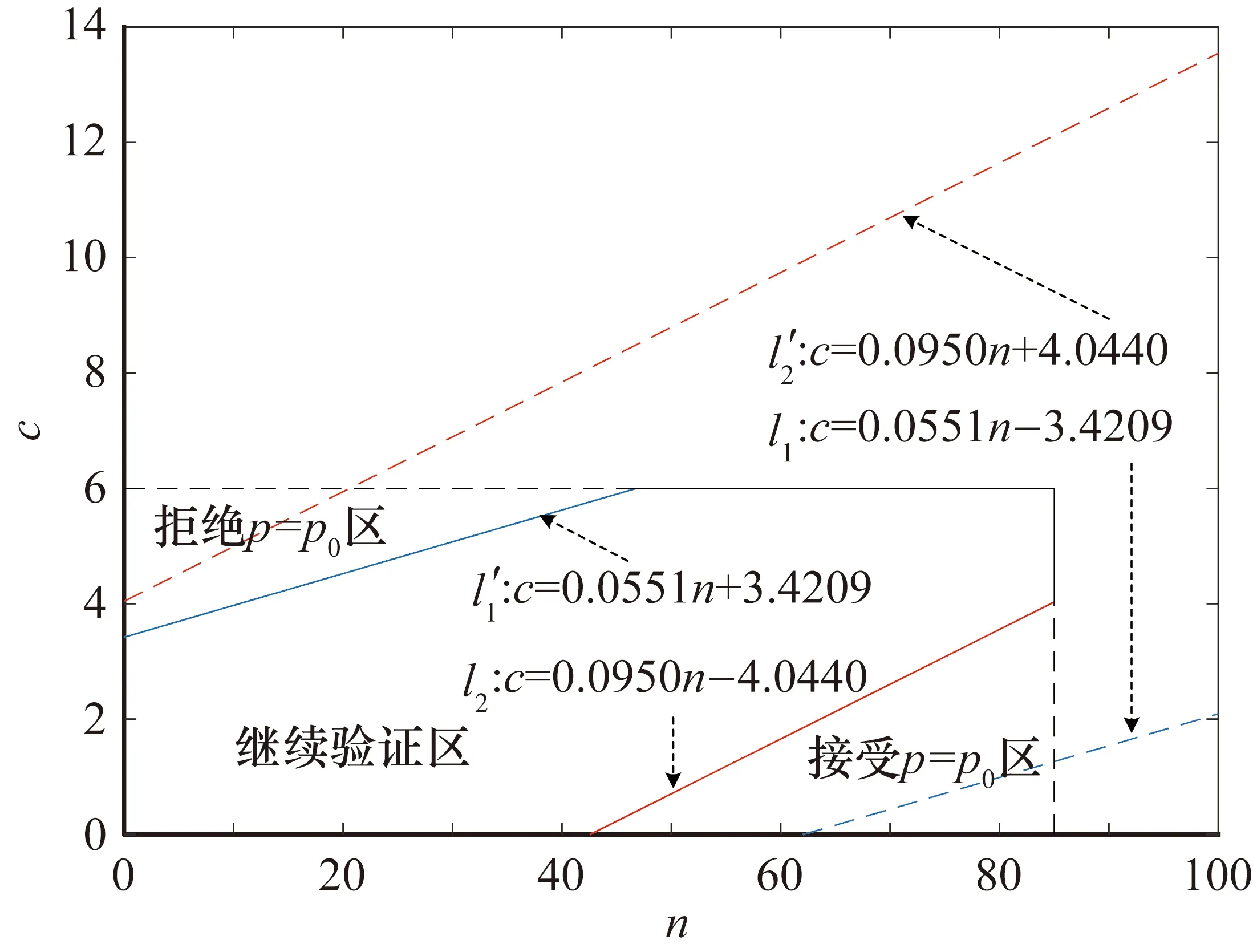
图4 某型装备测试性验证截尾序贯网图检验

4.2 对比分析

① 经典测试性验证方案。按照式(2)的不等式约束，可以求得经典验证方案为(76,5)。

② SPRT测试性验证方案。采用Monte Carlo仿真方法，将测试性指标值在(0,1]分为1000个离散值进行仿真，同时设置仿真次数为1000次，得到当指标值为0.937时，平均样本量的最大值为62.2024。

③ SMT测试性验证方案。根据4.1节得到的一系列设计参数，同样通过Monte Carlo方法(仿真参数保持一致)进行仿真，可以得到当指标值为0.957时，平均样本量的最大值为54.3162。

3种验证方案的平均样本量对比曲线如图5所示。

从图5可以看出，根据不同的指标值p可以确定验证试验的平均样本量，如本文提出的SMT测试性验证方案中，当p=p0时，ASN|p0=53.5244，当p=p1时，ASN|p1=39.0582。此外，从图中可以直观地反映出在指标p0和p1之间，所提方法平均样本量优于经典验证方案以及SPRT验证方案。

图5 平均样本量曲线对比

由此可见，该方案能保证验证试验开展前对试验最大样本量有一个直观的认知，同时能有效降低验证试验所需平均样本量，证明了该方案的有效性。

5 结束语

针对SPRT测试性验证方案最大样本量无法控制的问题，通过插入检验点的方式使得在测试性验证试验开展前能确定最大样本量，进而对试验的开展有比较客观的认知。在此基础上，考虑了所确定的最大样本量较大时的截尾策略，并通过实例分析证明本文设计的基于SMT方法的测试性验证试验方案较经典验证方案和SPRT验证方案在最大样本量以及平均样本量方面均有有效改进，对导弹类高精度武器装备的测试性验证试验的开展具实际指导意义。