基于广义奇异值分解的图像去噪算法

杨 洁， 魏平俊， 张旭初

(1. 中原工学院 电子信息学院， 河南 郑州 450007；2. 武警河南省总队 信息通信处， 河南 郑州 450018)

噪声会导致图像质量的下降，不利于对图像信息的解释。因此，图像去噪技术早已成为图像处理领域的研究热点，相关学者提出了多种图像去噪算法。例如，JAIN等将一种卷积神经网络应用于图像去噪[1]；许丽、刘波和熊新兵等提出了利用奇异值分解技术去除图像噪声的方法[2-4]；张雯雯等提出了非局部自相似性的图像去噪算法[5]；闵莉花等提出了基于偏微分方程的图像去噪算法[6]；王红宇等提出了基于中值滤波的图像去噪算法[7]。上述图像去噪算法虽然都能在一定程度上达到降噪的目的，但是降噪对象都是经典的二阶数组，属于经典的低阶图像，均未涉及高维空间信息。为了进一步提高高阶图像的去噪质量，本文提出一种基于广义奇异值分解的图像去噪算法，拟首先对原图像添加椒盐噪声，其次对含噪图像进行邻域变换，使其成为高阶含噪图像[8-10]，然后通过Matlab编程求解峰值信噪比，最后比较本文去噪算法与传统奇异值分解技术的图像去噪效果。

1 广义奇异值去噪方法

1.1 矩阵奇异值分解

奇异值分解(Singular Value Decomposition，SVD)是一种重要的矩阵分解技术，它以对称的方式处理矩阵的行和列，并对信息进行“排序”，在数据挖掘和其他方面都有重要作用[11-12]。传统SVD是利用A=U×S×VT进行分解的，分解对象为经典二阶矩阵。

由文献[3]可知，假设A是一个m×n阶矩阵，其中的元素全部属于域K，也就是实数域或复数域，则存在一个分解，使得

A=U×S×VT

(1)

式中：U是m×m阶酉矩阵；S是半正定m×n阶对角矩阵；V是n×n阶酉矩阵。这样的分解就称作A的奇异值分解。S对角线上的元素Si即为A的奇异值，且按从大到小的顺序排列。

1.2 广义奇异值分解

为得到更好的图像去噪效果，本文充分利用图像的高阶信息，在传统奇异值分解的基础上，提出一种基于广义奇异值分解(Tensorial Singular Value Decomposition，TSVD)的图像去噪算法。该算法主要通过邻域选取法对传统矩阵进行扩展，使其成为高阶广义矩阵，以达到图像去噪的目的。

假设存在一个广义矩阵Xt∈CD1×D2，满足：

(2)

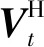
相比于传统SVD分解，TSVD分解的优势在于：分解对象可以是三阶、四阶甚至更高阶数组，而不仅限于传统矩阵。其具体方法可参照文献[8-10]。

若给定一个秩为r的矩阵，在对矩阵进行奇异值分解时，舍弃S中奇异值为零或奇异值较小的数值(因为零奇异值或较小奇异值所包含的信息较少，甚至在矩阵重建时可以忽略不计)，则广义奇异值可写为：

(3)

1.3 广义奇异值分解去噪原理

在图像处理中，准确完整的图像信息通常是不包含噪声的。若一副图像的秩偏高则是因为噪声的存在。进行矩阵的奇异值分解可以达到图像去噪的效果，但是效果并不理想。本文提出的基于广义奇异值分解的图像去噪算法是在传统奇异值分解去噪的前提下，首先利用广义矩阵模型，对原含噪矩阵进行高阶扩展[8-10]，然后采用广义奇异值算法进行去噪处理，最终得到去噪后的近似图像。

第一步：获取原图像，并对其添加高斯噪声；

第二步：对含噪图像进行邻域扩展，使其成为高阶含噪图像；

第五步：求取传统奇异值分解与近似广义奇异值分解得到的峰值信噪比，比较两者的去噪效果。

根据SVD重构原理，在已知一个矩阵的前提下，可以通过奇异值分解，选取较大的奇异值来代替原矩阵。在图像处理领域，可将上述理论应用于图像去噪。现实中很多图像一般是低秩的，因为噪声的存在，才形成了满秩矩阵[9]。因此，可通过SVD分解得到奇异值矩阵，对其进行简化，达到降噪的目的。

2 实验与仿真

为评估广义奇异值分解的去噪性能，以采用wikipedia下载的Lenna图像、MonaLisa图像及House图像为测试样本。图1所示为3种测试样本的原图像、噪声图像、加噪后图像、传统去噪后图像及利用本文广义奇异值分解去噪后图像的对比。

(1) 原图像 (2) 噪声图像 (3) 加噪后图像 (4) 传统去噪后图像 (5) 本文算法去噪后图像 图1 3种测试样本的图像对比

为了解广义奇异值分解在图像去噪方面的优势，对Lenna图像、MonaLisa图像及House图像，分别进行3×3邻域(TSVD)及3×3×3×3邻域(TTSVD)扩展，使原始的二阶矩阵扩展为四阶、六阶甚至更高阶矩阵(也称广义矩阵，具体定义可参考文献[8])。经统计分析，本文提出的广义奇异值分解算法在图像去噪方面明显优于传统奇异值分解算法，且其去噪能力与广义矩阵的扩展阶数成正比。这里以MonaLisa图像为例，比较扩展为四阶和六阶时图像的去噪效果，以峰值信噪比作为评价标准，峰值信噪比越大，图像的去噪效果越好(见图2)。

图2 传统矩阵与扩展为四阶和六阶时图像的去噪效果

本文共进行3个主实验：实验1为对原始图像加噪声，然后利用SVD进行降噪并求取峰值信噪比；实验2是将原始含噪图像进行3×3邻域扩展，使其成为四阶广义矩阵，然后利用TSVD进行降噪并求取峰值信噪比；实验3是将原始矩阵进行3×3×3×3邻域扩展，使其成为六阶广义矩阵，然后利用TTSVD进行降噪并求取峰值信噪比。其中，TSVD与TTSVD均表示广义奇异值分解，区别在于前者进行3×3邻域扩展，为四阶广义矩阵，而后者进行3×3×3×3邻域扩展，为六阶广义矩阵。

由图2可知，随着扩展阶数的提升，图像峰值信噪比增大，即图像的去噪效果越来越好。由此可得出以下结论：利用本文广义奇异值分解技术得到的图像去噪效果明显优于传统的奇异值分解技术，且矩阵的扩展阶数越高，图像的降噪效果越显著。

3 讨论

对原始含噪图像中每个像素点取一定范围邻域，且不断增加其维数，能够使高阶图像的重建质量不断提高。原始含噪图像的像素大小具有一定限制，且均以零元素进行填充。随着邻域的不断扩展，当所取像素点邻域均不在原始图像范围内时，再选取邻域已失去计算价值，所进行的低秩近似结果则逼近于极限值。例如选取一个5×5的矩阵，当从中心像素开始取邻域时，可最快到达极限。以a3，3为例，不断对第一个元素进行3×3邻域选取，当取到第六个3×3邻域时，所扩充的元素均不在元素图像的像素范围内，此时再进行邻域选取便失去实际意义。

4 结语

为验证所采用的广义奇异值分解技术在高阶图像分析中的应用效果，根据广义奇异值分解的相关理论，对多个测试样本进行了验证与统计分析。实验结果表明，在高阶图像去噪方面，广义奇异值分解算法与传统算法相比，图像的低秩重建效果具有明显的优势；针对高阶图像去噪，采用广义奇异值分解技术比传统奇异值分解技术所求峰值信噪比优势更明显，且其峰值信噪比随着矩阵扩展阶数的提升而增大。

本文提出的去噪算法充分考虑了图像的高阶信息，比传统算法更快捷、准确。将其应用于图像去噪，效果良好。