粘滞阻尼墙对高层建筑结构抗风性能影响的研究

闫安志， 杨 蕾， 王 磊

(河南理工大学 土木工程学院， 河南 焦作 454000)

随着当前经济水平不断提高，我国城市发展十分迅速，导致很多城市建筑密度过大。如何更好地利用有限的土地资源，成了一个十分严峻的问题。目前，很多城市都是通过建造高层和超高层建筑来解决这个问题。但是在建造高层和超高层建筑时，不可避免地要采用新技术和新材料。这就使得建筑逐渐向更柔，更高的趋势发展[1]，从而降低结构的刚度。另一方面，风荷载会随着建筑高度的增加而增大。这两个因素，都使得风荷载对高层建筑结构的振动响应过大，严重影响结构安全[1]。因此，高层建筑结构抗风设计显得格外重要。

近年来，各国开始将粘滞阻尼墙作为控制建筑结构振动响应的新型装置，许多专家学者对该装置的减振效果进行了理论分析和实验研究。 ARIMA等对五层钢框架结构缩尺模型进行了振动台实验，发现设置粘滞阻尼墙后，建筑结构的动力响应得到明显的控制[2]；YEUNG等对设置粘滞阻尼墙的建筑模型进行了风洞实验，并分析研究了粘滞阻尼墙处于扭转状态下的动力性能，发现粘滞阻尼墙能有效减小风振对结构的影响[3]；白丽通过算例分析了设置粘滞阻尼墙的框架结构与无控状态下的框架结构的动力响应，发现粘滞阻尼墙对结构起到了良好的减振控制[4]；杜东升等在对粘滞流体阻尼墙的减振分析中，设置了实际工程中应用粘滞流体阻尼墙的设防目标，提出了阻尼墙的设计流程及布置原则，并将其成功应用到一幢处于高烈度区的高层建筑中[5]。当前，建筑结构的振动控制研究主要集中在耗能减振装置的利用，研究的重心是风荷载对结构的影响，但是通过增设控制装置进行的高层建筑抗风性能研究并不完善。粘滞阻尼墙作为耗能减振装置的一种，在国外已经得到一定的研究和应用。但在我国，其研究尚处于初始阶段，相关的资料少之又少[6]。所以，对设置粘滞阻尼墙的高层建筑结构抗风性能的研究显得十分必要。本文以某高层办公楼混凝土框架结构为例，研究粘滞阻尼墙对高层建筑结构抗风性能的影响。

1 工程概况和建模

1.1 工程概况和建模

本文选用的某高层办公楼共16层，50年一遇的基本风压为0.45 kN/m2，地面粗糙度为B类，高层混凝土框架结构的阻尼比为0.05。其结构平面尺寸为35 m×17 m，底层层高为 6.0 m，标准层层高为 3.3 m，总高度为 55.5 m，屋顶为平屋顶，结构外形如图1所示。

图1 框架结构有限元模型

采用有限元分析软件Sap2000建立16层框架结构的空间杆系模型，混凝土材料为C40，其弹性模量E=3.25×107kN/ m2，密度ρ=2 500 kg/m3，泊松比μ=0.2。其中，底层柱子的截面尺寸为800 mm×800 mm，其他层柱子的截面尺寸为600 mm×600 mm；框架梁的截面尺寸为400 mm×800 mm，其他次梁的截面尺寸为300 mm×600 mm；纵向受力钢筋型号为HRB400,箍筋等级为HPB300；楼板和屋面板厚度为120 mm。梁柱采用杆单元，楼板采用壳单元。整个框架结构关键节点796个、杆单元1 232个、壳单元480个，并且壳单元采用四边形网格划分。楼面恒荷载和活荷载分别取3.0 kN/m2和2.0 kN/m2。

1.2 结构固有特性

对有沾滞阻尼墙和无粘滞阻尼墙的办公楼结构进行模态分析，限于篇幅，这里只给出无粘滞阻尼墙结构的振型(见图2)。通过对比分析两者的频率和振型(见表1)，可以看出，两者前三阶周期基本相同，说明粘滞阻尼墙只给结构提供了阻尼，而几乎不提供附加刚度。

2 粘滞阻尼墙的工作原理及布置方案

2.1 粘滞阻尼墙的构造及工作原理

粘滞阻尼墙是由固定在上层楼面梁的内部钢板、固定在下层楼面梁的外部钢箱及内外钢板之间的粘滞阻尼材料组成，如图3所示。其中，1、2、3分别为上层楼面、粘滞阻尼墙和下层楼面。

(a) 第一阶

(b) 第二阶

(c) 第三阶图2 无粘滞阻尼墙的框架结构前三阶振型

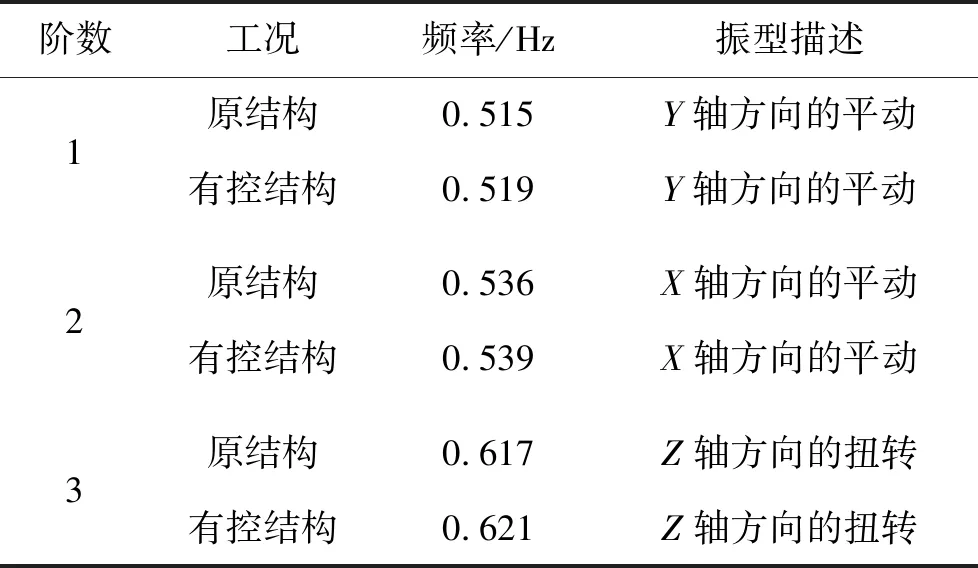
阶数工况频率/Hz振型描述1原结构0.515 Y轴方向的平动有控结构0.519Y轴方向的平动2原结构0.536 X轴方向的平动有控结构0.539X轴方向的平动3原结构0.617 Z轴方向的扭转有控结构0.621Z轴方向的扭转

图3 粘滞阻尼墙构造图

在风荷载作用下，结构上、下楼层之间产生相对位移或相对速度，此时，内钢板与内部粘滞液体发生剪切作用，通过产生的阻尼力来逐步消耗振动的能量，从而减小结构的风致响应，以便达到耗能减振的目的[7]。

在SAP2000中，粘滞阻尼器单元采用的是 Maxwell 计算模型，阻尼单元与弹簧单元串联。其力学计算模型如图4所示。

图4 粘滞阻尼墙力学计算模型

根据Miyazaki&Arima公式，忽略刚度的影响，对模型进行简化[8]，得到总粘滞抵抗力的公式：

F=CVα

(2)

式中：F为总粘滞抵抗力；C为阻尼系数；V为阻尼器两端相对线速度；α为阻尼指数， 取值范围一般在0.2～1.0之间。阻尼指数α对粘滞阻尼墙的减振效果有很大影响[9-10]。

依据参考文献[11]，选取的参数值如下:α为0.45，C为2 000 kN·s/m。为保证计算效率，弹簧刚度取2×105kN/m。

2.2 粘滞阻尼墙的布置方案

粘滞阻尼墙的具体安装位置参考文献[9]。以下4种工况均是在建筑结构侧面的第一榀和第五榀框架中分别布置粘滞阻尼墙，其布置位置如图5所示。工况一：布置28片粘滞阻尼墙，采用隔层布置方案，其他工况均布置36片粘滞阻尼墙；工况二：采用配置两层隔一层的布置的方案；工况三：采用下部集中配置的布置方案；工况四：采用中、上部集中配置的布置方案。

(a) 工况一 (b) 工况二 (c) 工况三 (d) 工况四图5 粘滞阻尼墙布置方案

3 脉动风数值模拟

3.1 高层结构顺风向脉动风响应

风荷载模型包括平均风和脉动风模型。平均风模型只考虑了结构的静力变形，未考虑结构的惯性力，计算结果与实际情况有一定差距；脉动风模型模拟出随机风压的时程，考虑了结构的动力特性，与实际情况拟合较好。故本文采用脉动风模型进行模拟[10-13]。

在脉动风荷载作用下，设置粘滞阻尼墙的结构的振动微分方程可表示如下[12-13]：

(3)

其中，fΓ可表示为：

(4)

式中：nj为布置在第j层的阻尼墙的数量；Pj为阻尼墙的水平输出力。

(5)

式中，θj为第j层的阻尼墙的水平夹角，θj=0。

设振型位移y为：

y=[φ]{q}

(6)

式中：[φ]为各自由度振型矩阵；{q}为广义坐标矩阵。

对式(6)进行正则化处理，阻尼采用瑞利阻尼，则第j阶振型运动方程表达式可写为：

(7)

式中：ζj为第j阶振型阻尼比；ωj为第j阶振型固有频率；Fj(t)为广义脉动风荷载。

(8)

式中：w(x,z,t)为脉动风压(kN/m2)；B(z)为建筑物z高度处的迎风面宽度(m)；H为建筑物总高度(m)；m(z)为建筑物z高度处线长度分布质量(kg)。

则位移响应y(z,t)可表示为：

(9)

3.2 风荷载模拟

本文采用线性滤波法中的自回归(AR)模型，选择 Davenport 谱作为目标谱，运用大型数值模拟软件 MATLAB编写模拟程序，对各加载节点脉动风速时程进行模拟，得到脉动风速曲线[14-15]。

模拟过程相关参数如下：①根据《荷载规范》(GB50009-2012)，确定工程所在地50年一遇的基本风压为0.45 kN/m2，算得10 m高度处风速为26.8 m/s；②自回归阶数p=4；③时间总长t=600 s，时间步长Δt=0.1 s；④截止频率Δf=10 Hz，频率步长Δf=0.01 Hz；⑤与地貌有关的地面阻力系数为0.003；⑥相干函数的公式为[15]：

(10)

式中：Cz为衰减系数，一般取Cz=10；v为离地面10 m高度处的平均风速；r为各楼层相对于距地面10 m高度处的距离；n为脉动风速的频率。

图6所示为建筑25.8 m高度处的风速时程曲线图，模拟得到的脉动风功率谱与目标谱的比较情况如图7所示。由图7可以看出，采用AR模型模拟出的脉动风速时程曲线，其功率谱与目标谱拟合良好，仅在高频段稍有偏差，表明该模拟方法具有较高的精度。

在模拟得到风速时程的基础上，通过式(11)将风速时程转换成风压时程，再乘以相应高度处的体形系数和受风面积，就可以得到模拟风荷载时程曲线[16]，如图8所示。

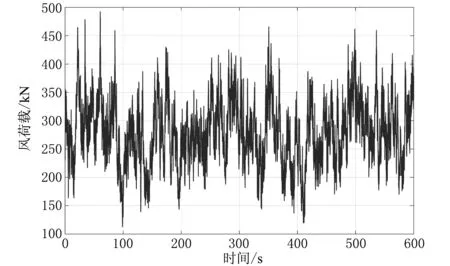
图8 脉动风荷载时程曲线图

风速与风荷载转换公式为：

(11)

式中：V(z,t)和F(z,t)分别为z高度处的风速和风荷载时程；μz和Az分别为z高度处的体形系数和受风面积。

4 粘滞阻尼墙的减振效果分析

4.1 不同工况下粘滞阻尼墙的减振效果对比分析

表2所示为在50 年一遇基本风压下，4组工况下的建筑结构顶层位移和加速度时程响应的对比分析情况。

由表2可知，工况二的布置方案优于其他3种方案。下面针对工况二下有粘滞阻尼墙的结构和原结构进行进一步的动力学分析。

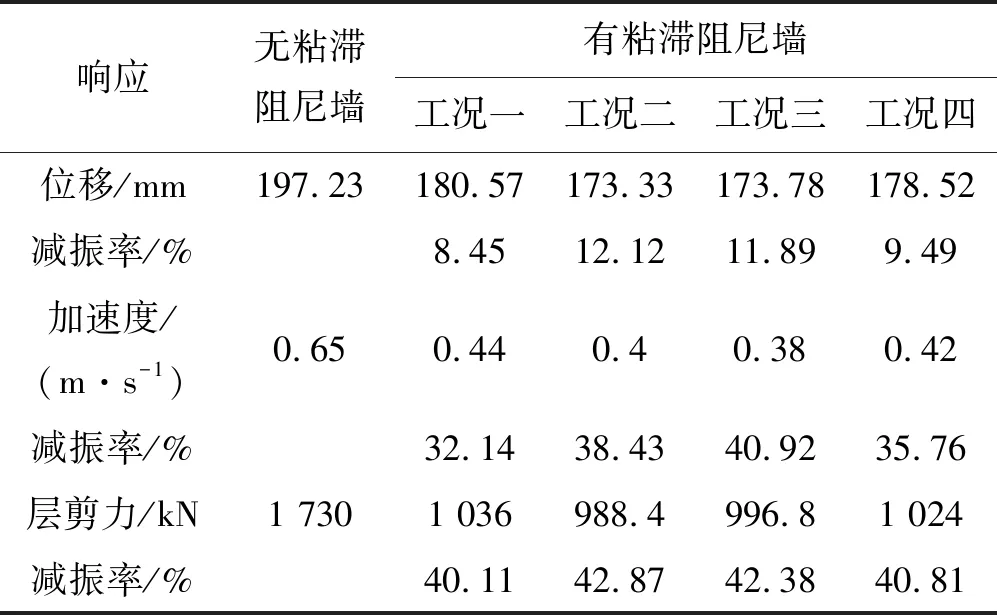
表2 不同工况下顶层最大响应

4.2 风荷载下结构的振动响应

图9所示为在脉动风荷载作用下，工况二下有粘滞阻尼墙的结构和无粘滞阻尼墙的结构各个动力学指标的对比图。由图9可知，工况二的顶层位移比原结构减少12.1%，随着层数的增大，层位移减小幅度逐渐增大；当风沿强轴方向时，最大层间位移角达到1/218 rad，比原结构降低约7.2%，层间位移角衰减幅度约为7%～24%；层加速度衰减幅度约为34%～79%；与原结构相比，设置了粘滞阻尼墙的结构的层间剪力均有明显减小，层间剪力降低最大约为42.9%。

在进行结构动力学响应模拟时，结构会因突然受到初始风压影响产生瞬态振动[17-18]。为清晰可见，图10和图11仅仅截取200～ 400 s 的顶层加速度和顶层位移的时程响应曲线，没有初始阶段。

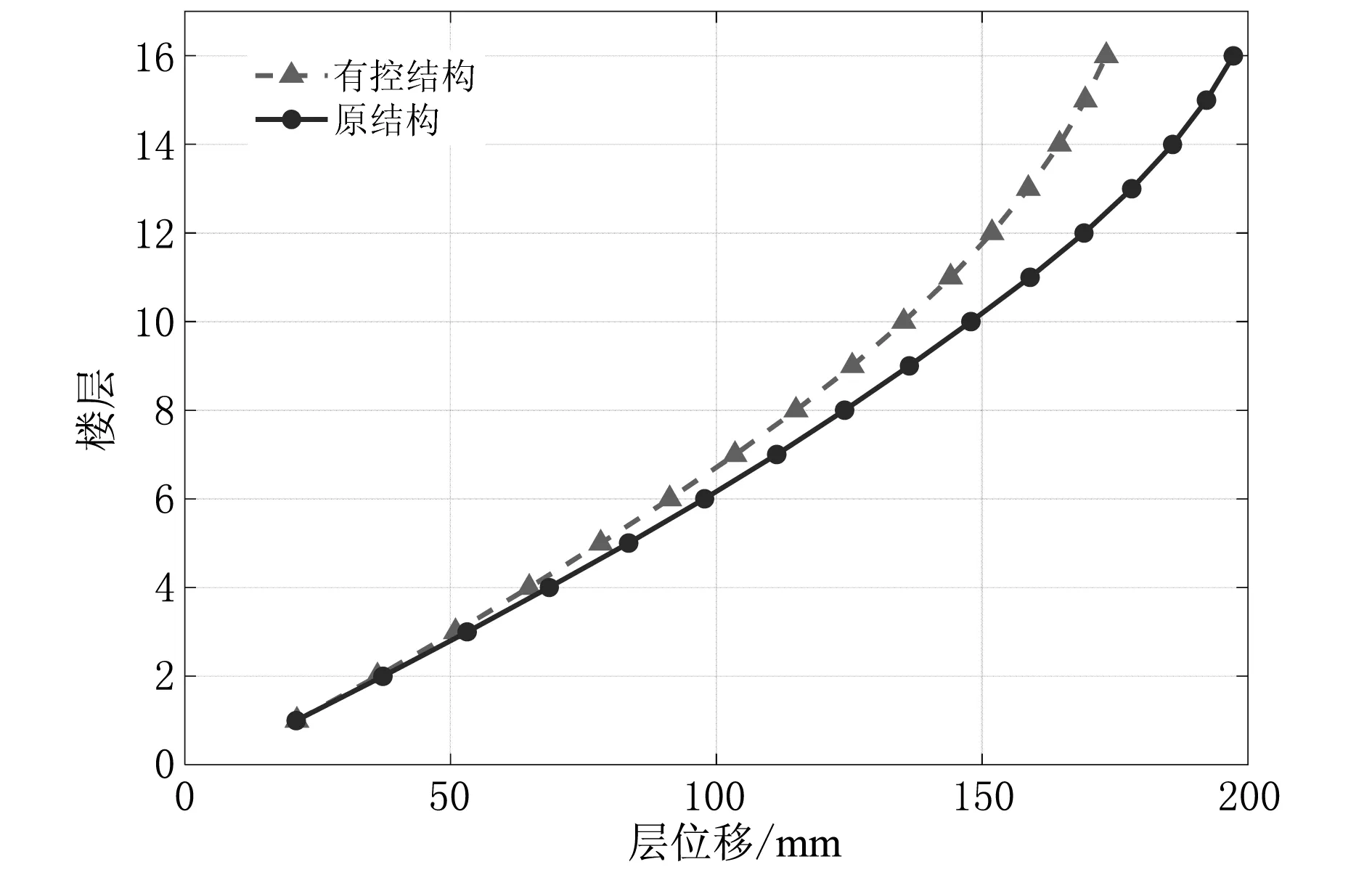
(a) 层位移对比

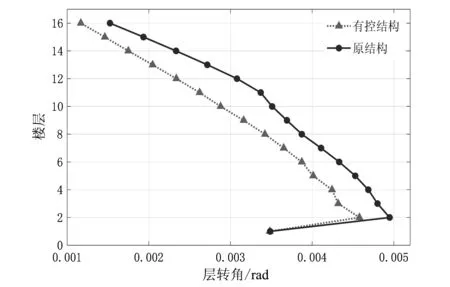
(b) 层间位移角对比

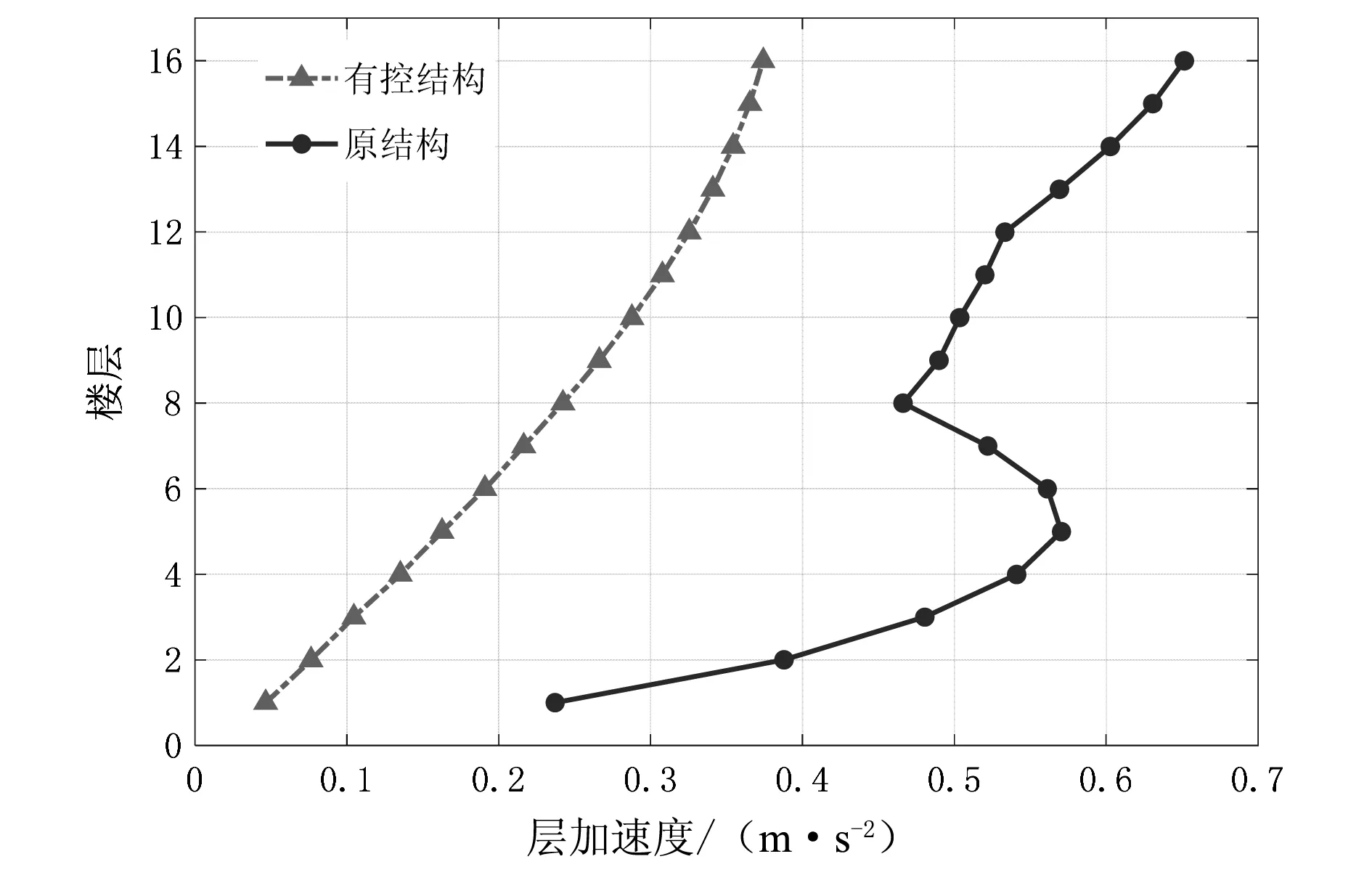
(c) 层加速度对比

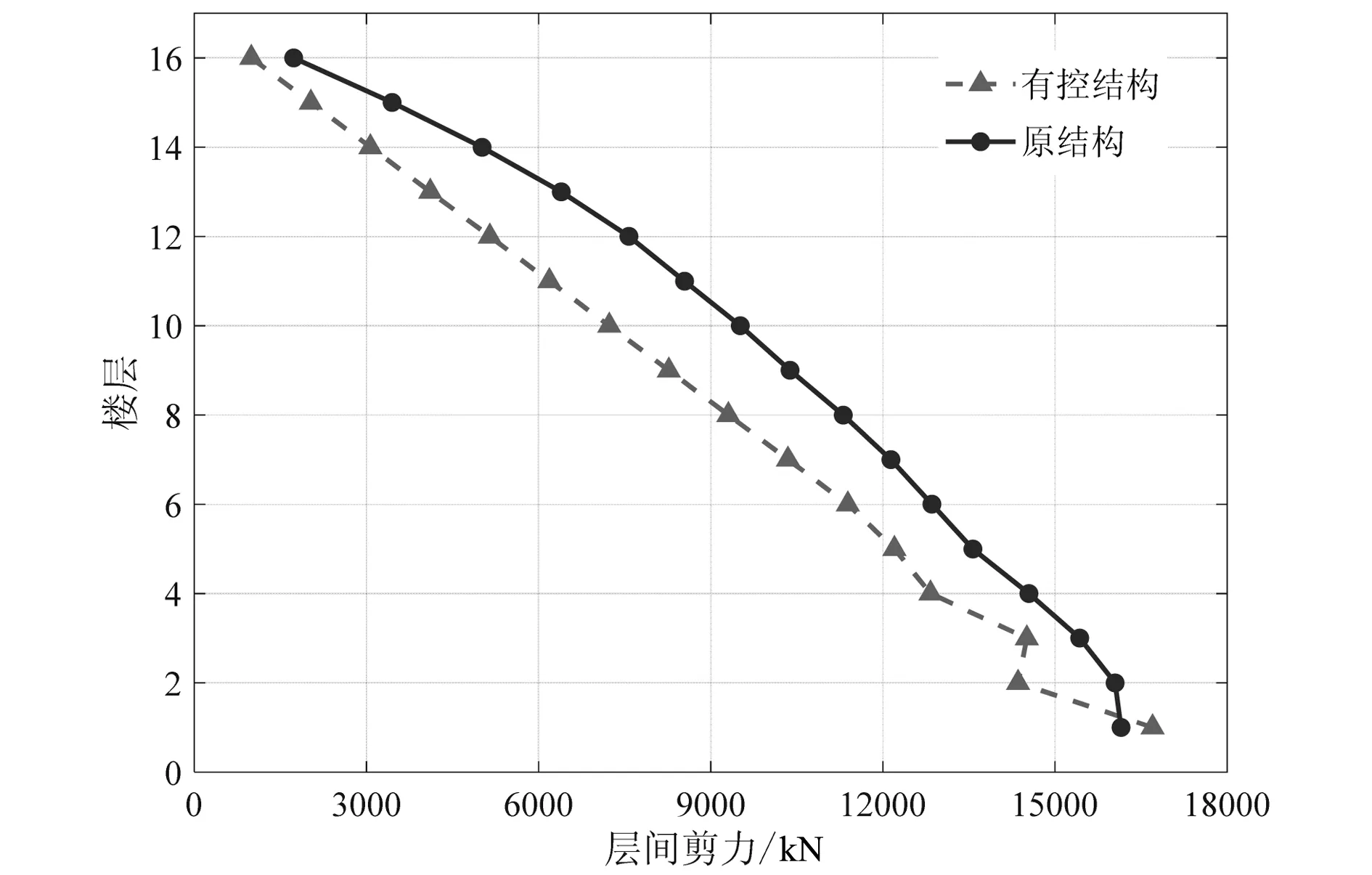
(d) 层间剪力对比

图9减振效果分析对比图

图10 顶层加速度对比

图11 顶层位移对比

由图10可以看出，在脉动风荷载作用下，无粘滞阻尼墙的结构的顶层最大加速度为0.651 m/s2,有粘滞阻尼墙的结构的顶层最大加速度为0.401 m/s2，下降幅度达到38.40%，这表明粘滞阻尼墙可大幅度降低结构的顶层动力响应。由图11可以看出，无粘滞阻尼墙的结构和有粘滞阻尼墙的结构的顶层最大位移分别是197.23 mm和173.33 mm，最大位移减少12.1%。可见，采用粘滞阻尼墙的结构在整个时间历程上均能有效减小原结构的顶层位移响应。综上所述，该减振方案对结构的振动控制效果较好。

5 结论

本文以某高层办公楼混凝土框架结构为例，利用有限元分析软件SAP2000分析了有粘滞阻尼墙和无粘滞阻尼墙的建筑结构的固有特性，分析了两种结构在风荷载作用下的动力响应，探讨了风荷载下两种结构的层位移、层间位移角、层加速度和层间剪力，得出以下结论：

(1) 粘滞阻尼墙基本只提供结构阻尼，几乎不提供附加刚度；

(2) 粘滞阻尼墙能够明显减小建筑结构的层位移、层间位移角、层加速度和层间剪力，提高高层结构的减振性能；

(3) 设置了粘滞阻尼墙的建筑结构的顶层加速度和顶层位移均有较大幅度的下降，特别是对加速度的抑制效果明显；

(4) 粘滞阻尼墙可以提高高层建筑物的抗风性能和舒适度。