引信装定系统用模拟火控系统设计

魏亚伟，李豪杰，原红伟，于 航

(南京理工大学 机械工程学院，南京 210094)

新形势下战争不再是单一的某一个作战单元发挥作用去攻击敌方，而是与其他的作战平台交联成一个整体，实现信息交互[1-3]。其中，火控系统包括了武器系统中绝大部分的电子设备，也承载了武器系统中的通信控制、目标识别与跟踪、炮车控制、镜体控制、定位导航和传输显示等许多主要和关键的作战任务，是武器系统交互控制的汇聚点和核心，是武器现代化的标志[4]。而引信与火控系统之间的互联对攻击来袭目标或者杀伤敌方起到关键作用，通过在发射前、发射过程中、发射后对引信的装定，使得引信适时作用在最理想的时间、距离、方位引燃、引爆战斗部装药从而使弹药战斗部起到最大的杀伤效果，实现最佳的作战模式[5]。由于火控系统是发射平台的一部分，对于从事信息化引信研究的人员在研究信息交联时无法脱离火控系统实现独立测试与性能验证[6-7]。通过查阅资料，文献[8]提出了基于二维插值算法的引信用装定器弹道参数解算方法，满足精度的同时，也简化了计算，但是该方法运算速度慢，占用内存大，对射表的使用较复杂。文献[9]提出了当前军机广泛的使用指令响应型数据总线作为其多功能综合航空电子火控系统的数据传输和控制系统，并进行了仿真，但没有编写相应的上位机来满足实验室装定的需求。在编写人机交互界面的过程中，MATLAB强大的计算能力和界面设计功能使其成为主要的设计工具[10-11]。为此，通过对火控系统的分析，明确了实验室装定引信对火控系统解算信息，实时装定功能的需求，基于MATLAB软件，采用整体拟合法的数据处理手段，对导入的射表进行拟合，在输入外部环境信息的情况下，解算出装定信息，编写相应的人机交互界面程序来实现模拟火控的功能。

1 模拟火控系统设计

1.1 模拟火控系统的构成

引信装定系统用模拟火控系统需完成射表转换，参数输入，装定数据解算等三项功能。首先导入射表，然后通过输入炸点距离、海拔、气温、气压、风速、风向时可以得到引信预装定时间TPE1和速度修正系数K；最终把信息传送给装定器，装定器装定信息到引信。其中模拟火控系统为本文主要设计部分，并且满足炸点距离900 m的范围内，装定飞行时间误差小于1 ms,装定速度修正系数误差小于0.01 ms/(m/s)，其模拟火控装定工作流程框图如图1。

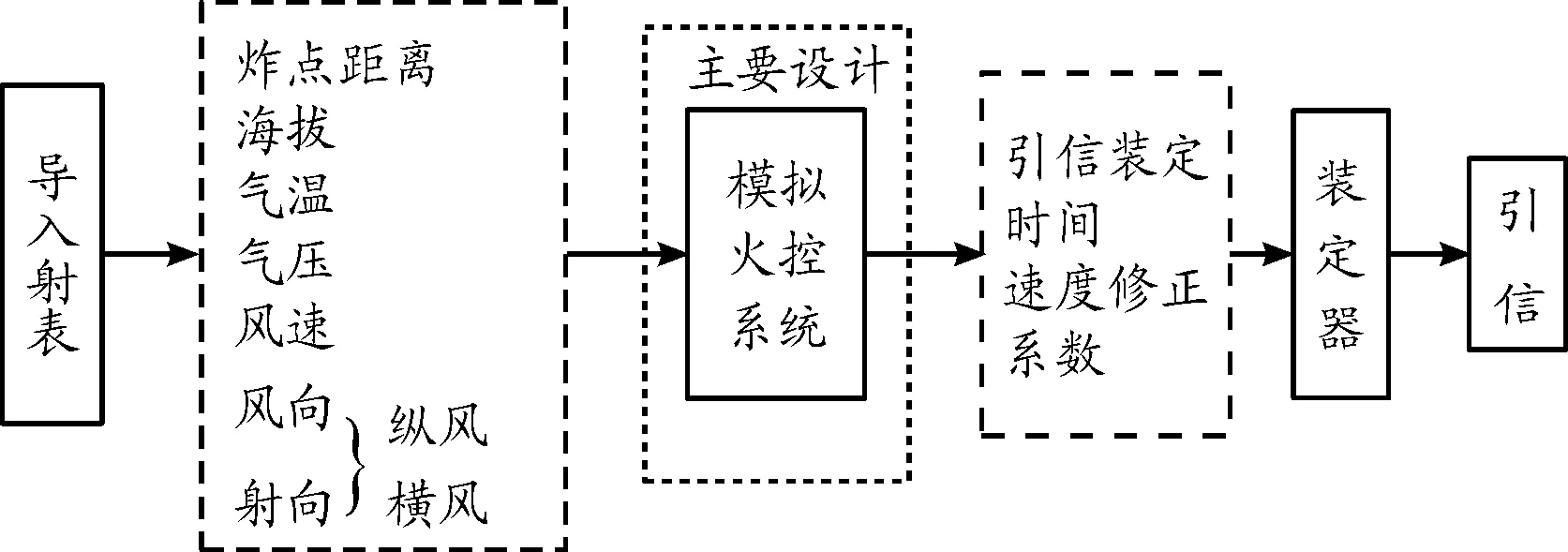
图1 模拟火控系统装定工作流程框图

而在系统程序中要包括对气温、气压的修正系数运算过程、纵风、横风风速的修正系数运算过程、速度修正系数的运算过程。

1.2 射表修正量使用方法

本文导入的射表即表1和表2，其中表1为某定距弹的飞行时间和速度修正系数与炸点距离的关系，表2反应了外部环境条件变化导致的装定时间变化量与炸点距离的关系。

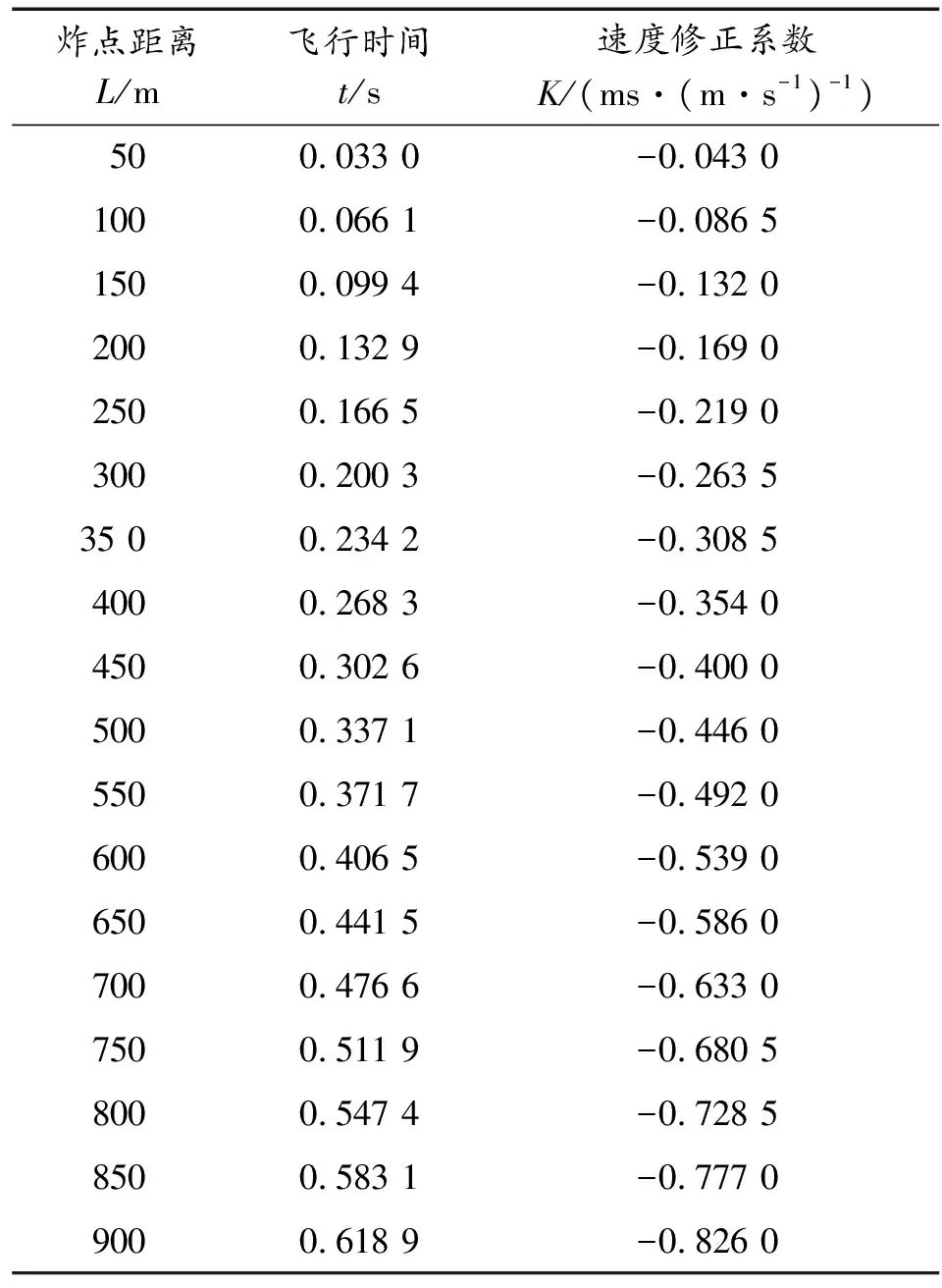
表1 某定距弹基本射表

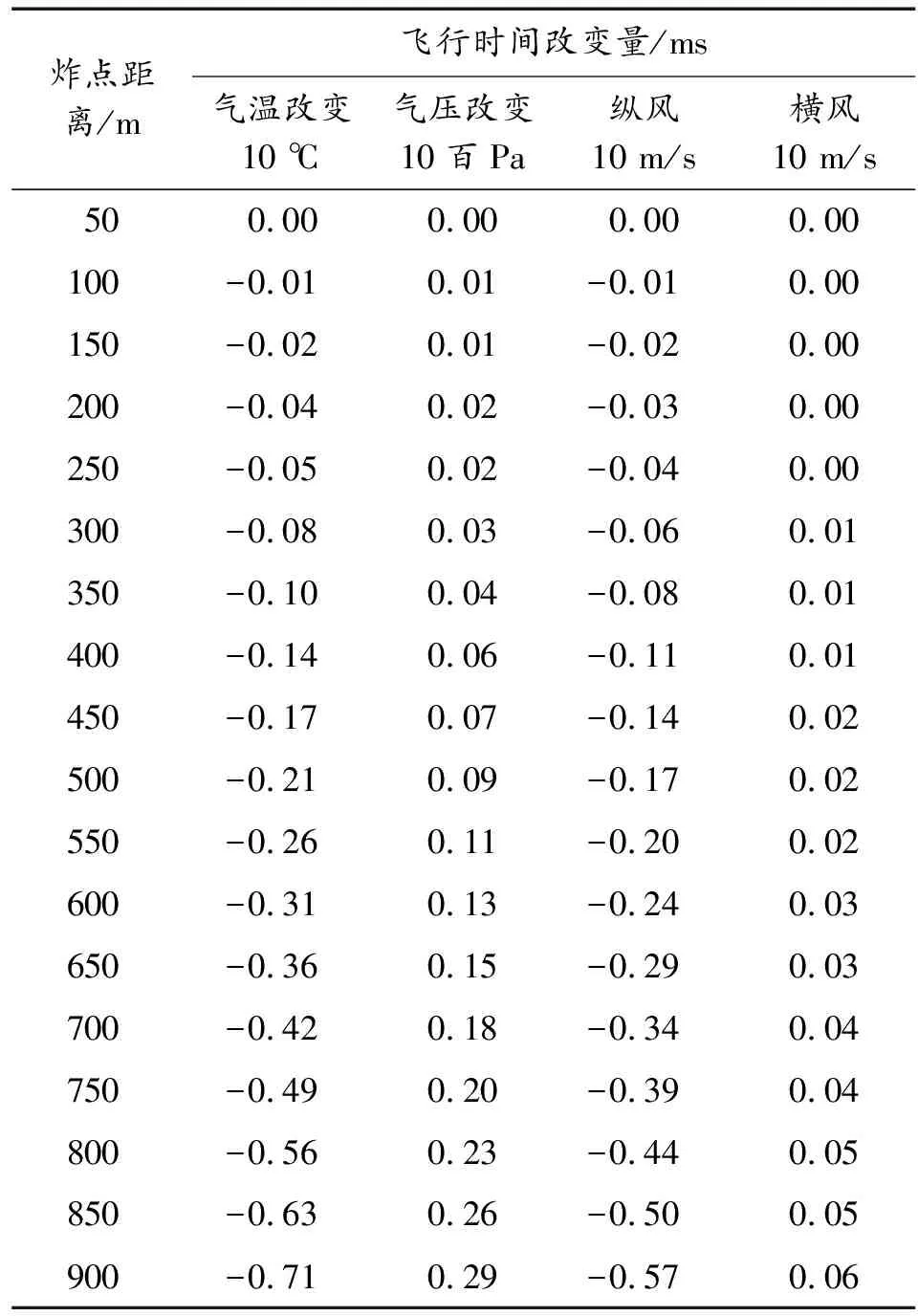
表2 某定距弹修正量表

引信装定系统用模拟火控系统最终输出计算结果有两个：一个是速度修正系数K，另一个是引信预装定时间TPE1。

引信预装定时间TPE1的计算式：

TPE1=T(L)+0.001E

(1)

式中：T(L)为射表中所列出对应射程L的飞行时间，查表1。时间单位(s)；E为射程L的时间修正量。时间单位(ms)。

时间修正量E的计算公式：

(2)

式中：Ki为对应修正系数；Δi为对应偏差量。

1.3 系统总体设计及程序流程图

在1.1节中明确说到引信装定系统用模拟火控系统的基本构成，由输入部分、控制部分、输出部分、其他部分组成。其中输入部分包括射表的导入，炸点距离，海拔及相关环境条件变化等信息；控制部分即为内部射表的拟合计算和装定给引信数据的解算；输出部分为解算数值的输出显示；其他部分为模拟火控系统标题的美化显示。

系统的总体在满足上述必须部分的基础上，尽可能简洁明了容易操作。根据设计要求和系统构成编辑出如图2所示界面，满足设计要求。

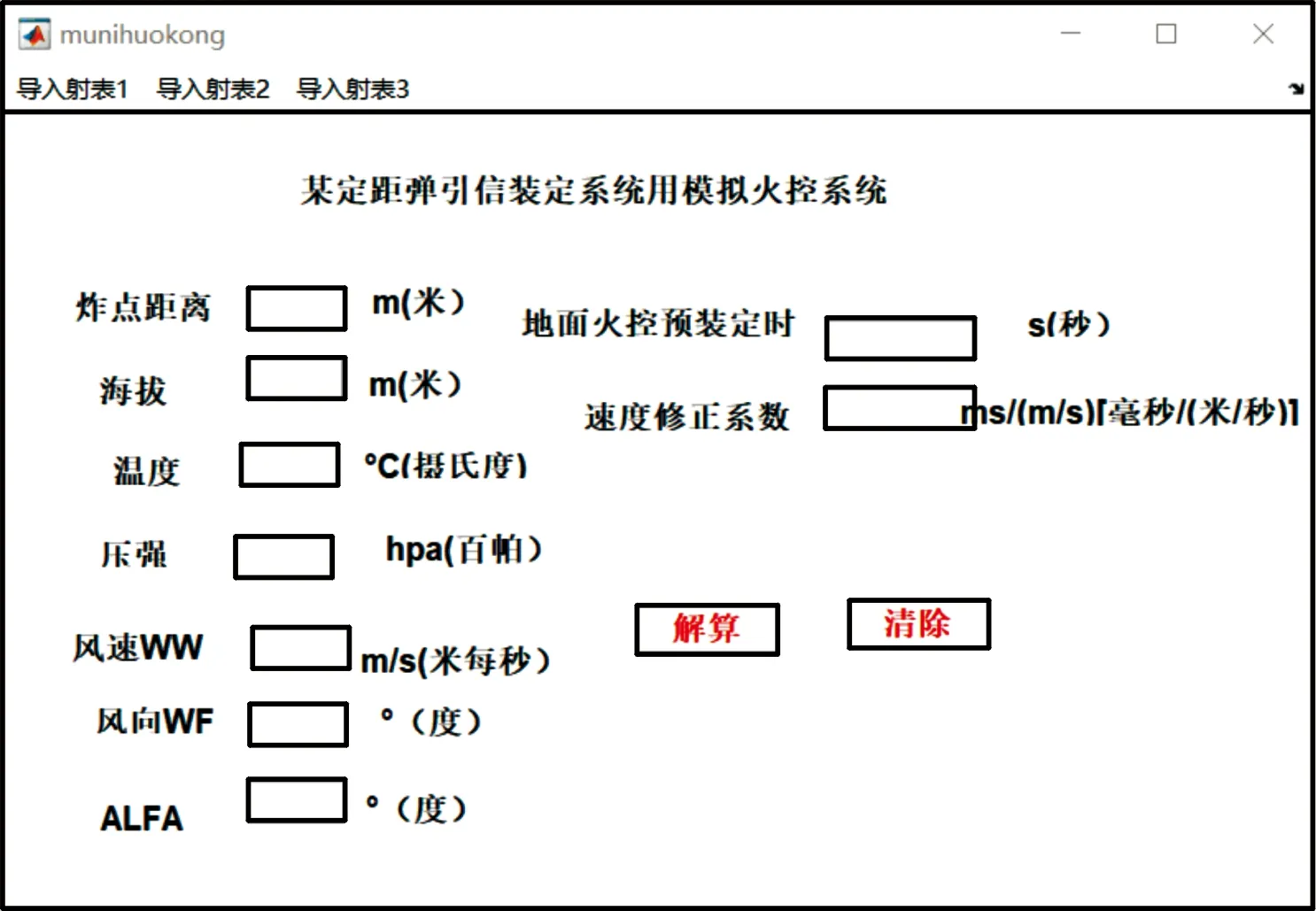
图2 引信装定系统用模拟火控系统界面

通过编写程序，实现上述界面的各个模块功能，运行程序的流程框图如图3。

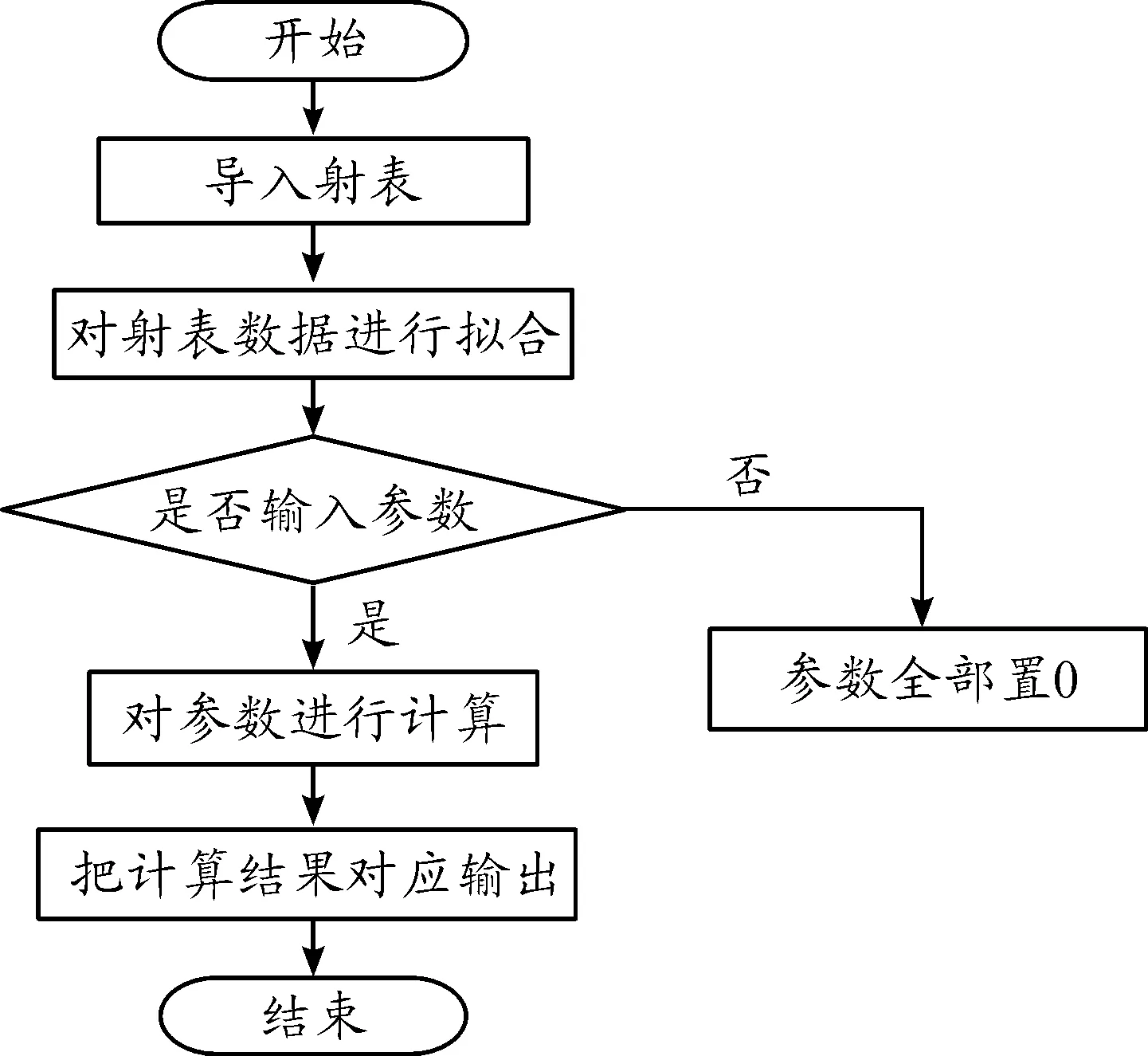
图3 模拟火控的程序流程框图

2 模拟火控的射表数据拟合

采用拟合法进行系统设计，是将射表导入到Matlab中，利用Matlab强大的计算能力，对导入的射表进行绘图，并对图像进行拟合，得到整体拟合公式，以下是对飞行时间、速度、气温、气压、横风、纵风等修正系数的拟合图像，并得到相关的拟合公式。其中气压、横风、纵风与前面图像类似，进行省略。

其公式如下：

1)飞行时间二次方拟合公式：

y=3.397 4e-08*x2+0.000 656 97*x+7.046 6e-5

其拟合图像如图4所示。

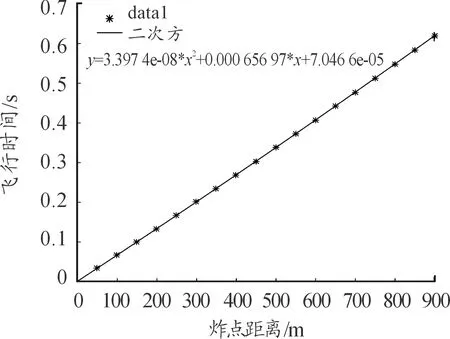
图4 飞行时间二次方拟合图像

2)速度修正系数二次法拟合公式：

y= -6.453 8e-08*x2-0.000 860 16*x+0.000 621 32

其拟合图像如图5所示。

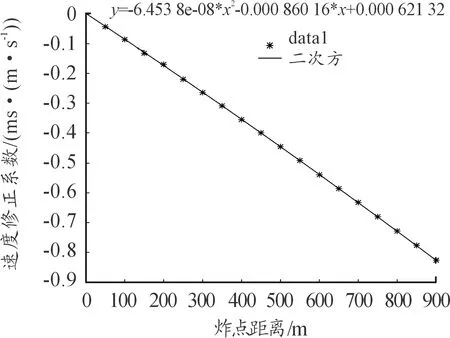
图5 速度修正系数二次方拟合图像

3)气温修正系数二次方拟合公式：

y= -9.151 2e-07*x2+4.500 8e-05*x-0.004 436 3

其拟合图像如图6所示。

3 模拟火控试验验证

根据射表中的数据(表1)，某定距弹在海拔高为340 m，气温变化5 ℃，气压变化500 Pa，无横风和纵风的情况下，模拟火控解算的装定数值如表3所示。

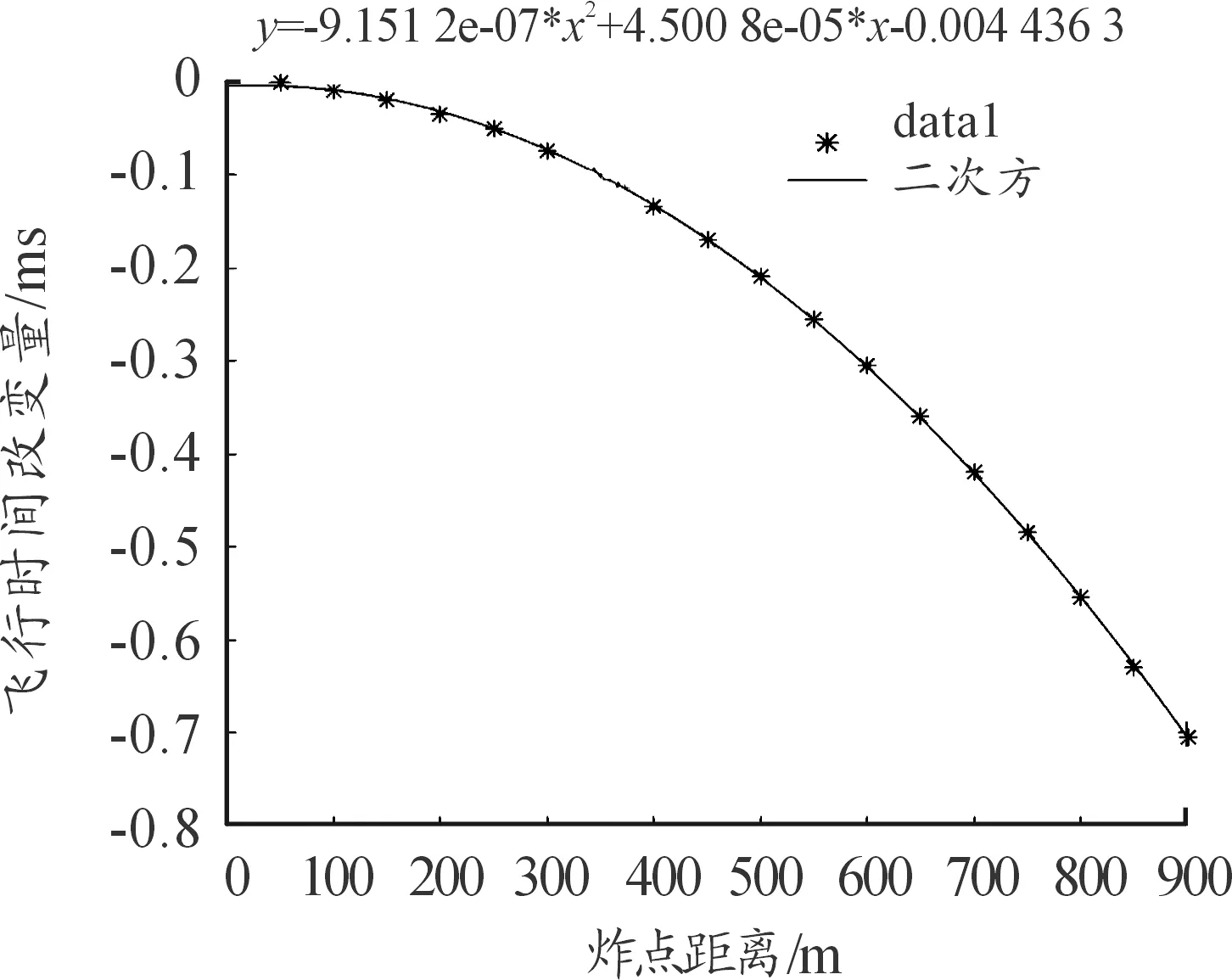
图6 气温修正系数二次方拟合图像

表3 模拟火控装定数值

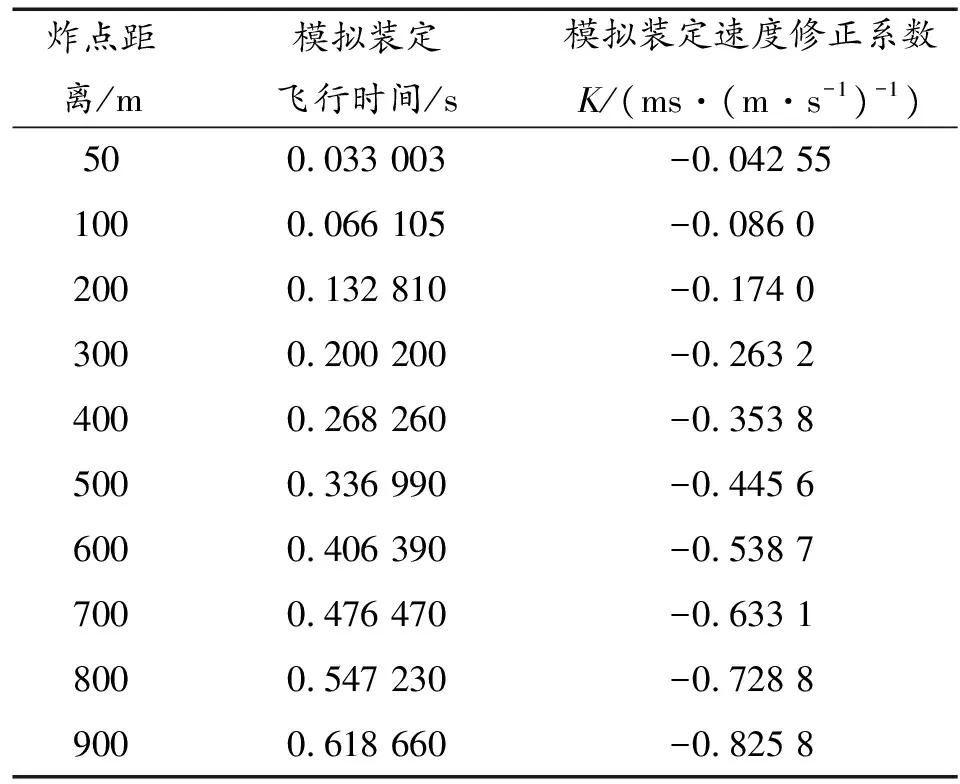
炸点距离/m模拟装定飞行时间/s模拟装定速度修正系数K/(ms·(m·s-1)-1)500.033 003-0.042 551000.066 105-0.086 02000.132 810-0.174 03000.200 200-0.263 24000.268 260-0.353 85000.336 990-0.445 66000.406 390-0.538 77000.476 470-0.633 18000.547 230-0.728 89000.618 660-0.825 8

与射表内的装定数值相比，其绝对误差如图7所示。

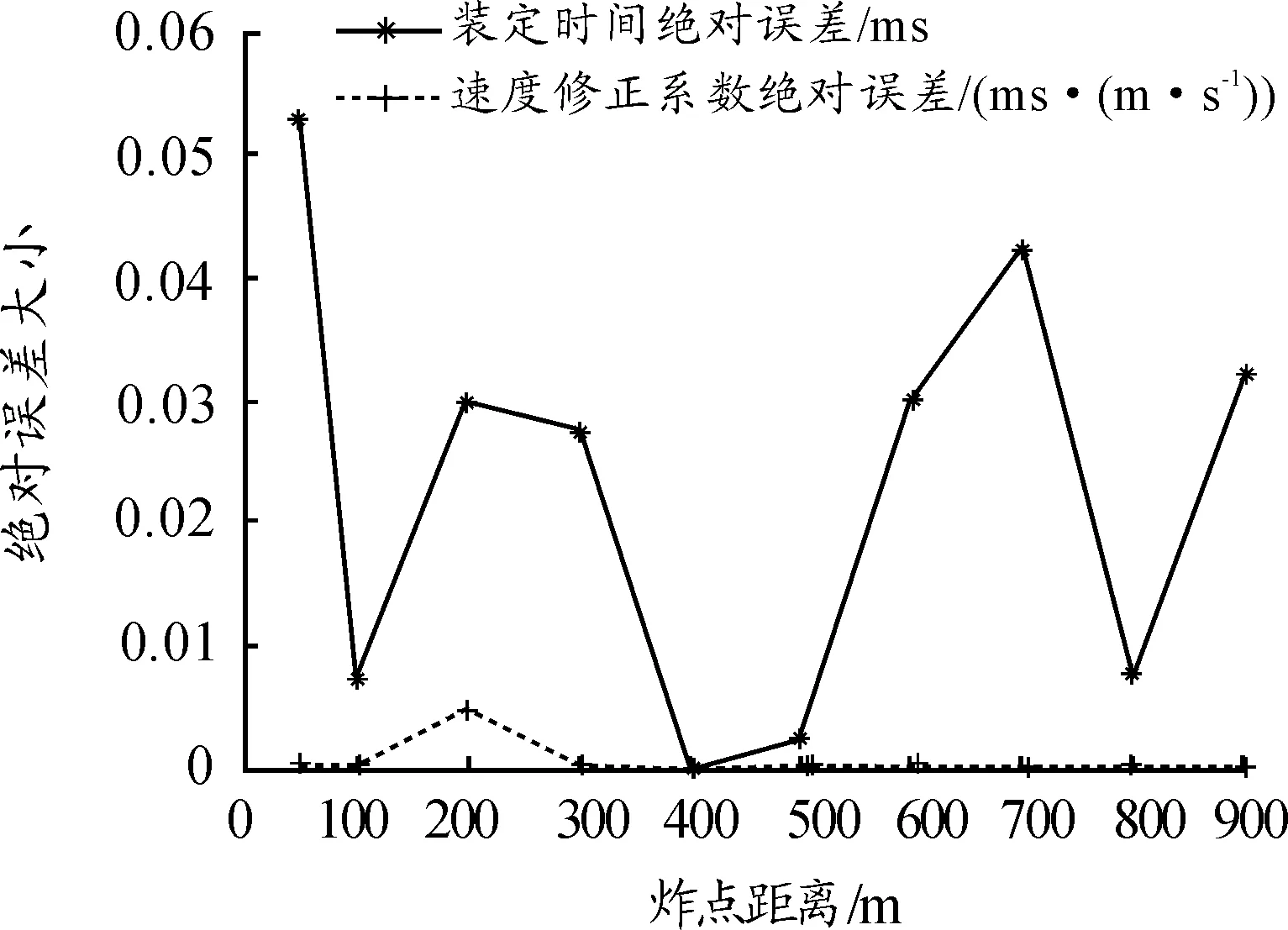
图7 模拟火控装定量的绝对误差示意图

由图7可知，在900 m的炸点距离内，装定时间的绝对误差最大为0.053 ms,小于1 ms,速度修正系数绝对误差小于0.01 ms/(m·s-1)，在误差允许的范围内，模拟火控的装定数值可满足测试功能与性能要求。

4 结论

本文为实现引信装定功能的实验室测试，在明确模拟火控系统设计需求的情况下，开展了模拟火控的功能分析与设计，并设计了模拟火控人机交互界面。基于工作流程分别设计各子系统程序模块。

子系统采用拟合法进行设计，通过对射表数据进行拟合计算，得到与炸点距离相关的函数，在数据处理时计算量少、满足精度要求。通过模拟火控试验验证，误差小，精度符合装定要求，为实验室可装定引信的设计和测试带来了极大便利。