火箭橇时空位置测试数据处理算法分析
2019-12-03王林安朱轶龙
王林安,付 宇,朱轶龙
(中国兵器工业试验测试研究院,陕西 华阴 714200)
伴随着世界新军事变革的不断发展与高新技术的广泛应用,现代战争的作战形态和作战理念正在发生深刻的变化,基于效果作战的战争效益观逐渐被世界各国所接受。精确制导武器以其快速、敏捷、高效、具有远程精确打击、命中精度高等特点,使其具有强有力的杀伤能力,是当今信息化高技术战争必不可少的主要武器。精确制导武器的关键技术在于制导系统,制导系统的精度决定着武器系统是否能够准确地击中目标。而卫星导航、惯性测量技术则成为提高中远程精确制导武器制导可靠性和实战能力最有效的导航模式。
在改进提高制导装置自身精度的同时,提供更为接近真实使用环境的试验测试条件,研究制导系统的天地一致性问题,最终提高使用精度,就成为一个重要的研究课题[1-2]。对制导系统进行客观有效的性能鉴定和评估考核,是降低制导武器定位误差、提高导航精度的基础,是提高精确制导武器制导可靠性和实战能力的必要环节。由于火箭橇试验技术在制导系统性能考核中具有不可替代的独特优势,近些年来,相关试验测试技术在国内进行了较为深入的研究和探索,其成果也得到了较好的应用。
1 制导系统性能考核的主要方法
目前,国内针对卫星、惯导等制导系统性能考核测试的主要方式有以下几种:
1)实验室测试。卫星制导系统的实验室测试方法主要有静态法、模拟法、公路跑车法等[3],后两种方法在一定程度上模拟了动态测量过程,可以对GPS、北斗制导系统接收机动态特性、软件处理精度等进行有限的考核,不足点是由于无法模拟实际的飞行环境,因此动态精度的考核不够充分,模型误差较大。
惯导系统的实验室测试方法有:重力场翻滚测试、振动台测试和离心机测试等。重力场测试,只能提供±1g的加速度输入,与加速度计实际工作环境有很大的出入,不能充分激励高次项误差系数;振动台测试只涵盖了加速度计真实工作环境高频区的一个小范围,且振动台测试多用于环境可靠性试验;离心机测试虽然分离加速度计误差系数,但是测试时间远大于加速度计实际工作时间,在提取高性能系统数据中产生的问题较多[4]。
2)飞行试验测试。飞行试验是考核导弹制导系统最直接有效的测试方式,通过雷达、光电、遥测等多种外测设备,对弹道数据进行测量和统计分析,以获取制导系统的性能参数。但是其存在试验成本高、安全风险大、实验数据样本有限等缺点,尤其在武器装备科研阶段,飞行试验不是最经济、最安全的系统考核方式。
3)火箭橇试验测试。火箭橇试验是介于实验室测试和飞行试验之间的一种“地面飞行试验”,可以使惯性测量装置受到高达约8个g的加速度和15个g的振动[5]。相对于实验室测试,其最大特点是:火箭橇所提供的力学环境更接近于真实环境,能够模拟产品所需要的速度,气流场、温度场更接近于自由场实际环境,且可以进行大尺寸产品1∶1试验,也便于各种测试仪器的布设。相较于飞行试验,能完全无损地回收到被试产品,供进一步测量分析,减小武器试验风险,同时具有较高的重复收集试验数据的能力,且测试数据获取相对容易,能够缩短产品研制的周期。
火箭橇试验技术就是在火箭发动机推力的作用下,试验装置能够在高精度轨道上高速滑行,以实现对被试产品进行动态性能考核的地面模拟试验技术。该技术目前已广泛应用于航空、航天、兵器以及高科技领域的科学试验,如精确制导、空气动力、航空弹射救生、引信、战斗部、穿甲、爆炸冲击等,这种试验技术能够弥补实验室测试和导弹飞行测试的空白[6]。美军大力神、宇宙神和民兵等洲际导弹的成功研制,在某种程度上要归功于非常成功的火箭橇试验,因此美国把火箭橇试验正式列入制导定位的试验大纲中,作为地面试验的最后阶段,并明确规定制导系统只有在火箭橇试验考核通过后才能进行飞行试验[7]。
依托火箭橇试验测试技术,利用获取的火箭橇运行过程时间-空间位置测试数据,解决惯性器件、卫星导航系统在高速度、高加速度等动态条件下导航定位性能的考核验证问题,在国内外目前是最佳的试验测试方案。兵器靶场在此项技术上通过长期的科研攻关,已经取得了明显的突破,并获取了大量有效的试验数据。
2 基于光电阻隔技术的火箭橇时空位置测试原理
针对火箭橇时空位置的测试,国内目前主要采用了磁电感应、光电阻断两种技术。磁电感应方法是利用火箭橇携带永磁钢,经过轨道上布设的若干霍尔开关传感器,产生计时脉冲信号,形成火箭橇运行全程的弹道基础数据[8-9]。这种测试方法存在的主要问题是:在几公里的范围内,传感器和数据采集系统需要布设数千路设备,系统复杂庞大,成本高,同时,系统动态响应延时误差较大,测试精度有限。采用光电阻隔技术进行火箭橇时空位置的测试方法,则有效解决了上述问题,得到了较好的应用[10]。
基于光电阻隔技术的火箭橇时空位置测试原理示意图如图1。首先需要在火箭橇轨道全程,建立米级间距的位置标,位置标采用圆柱型结构,位置标顶端设计为球窝型结构,用于安置精密测量靶球。
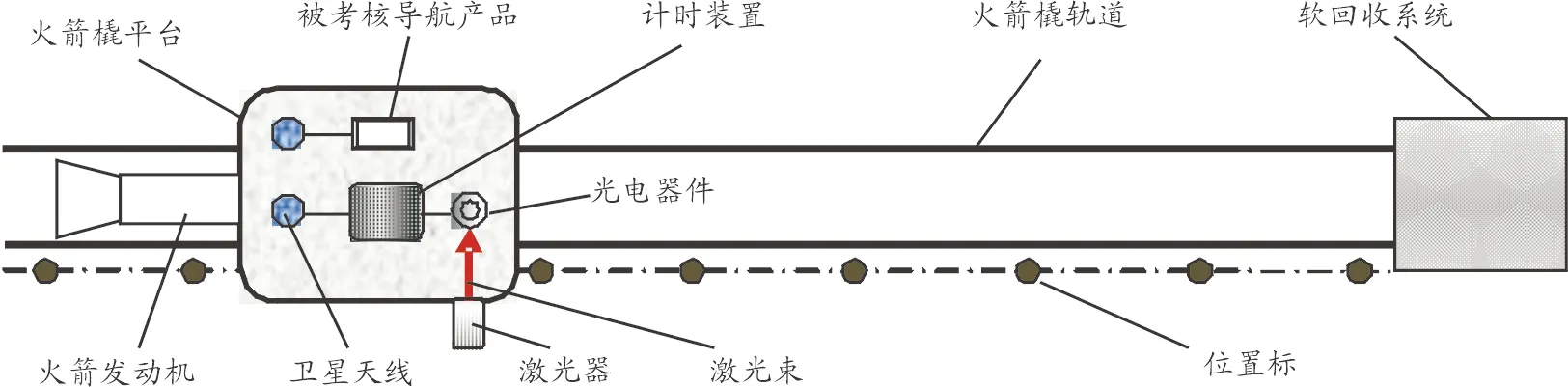
图1 基于光电阻隔技术的火箭橇时空位置测试原理示意图
位置标沿轨道方向的距离,采用高精度的电子全站仪和激光跟踪仪联合进行测量,全站仪的测量数据用于对激光跟踪仪的测量数据进行分段闭合平差,以提高位置标距离测量精度。
火箭橇平台上安装有光电阻隔探测的光电组件和计时设备,计时设备具有接收卫星UTC时间功能。火箭橇在轨运行过程中,当光电组件经过位置标时,会由于激光光路受到阻隔而产生计时脉冲信号,触发计时设备,记录火箭橇通过每一个位置标的精确时间信息,结合已经测量得到的位置标距离信息,就可以对火箭橇全程的运行轨迹进行精确处理[11]。
3 时空位置数据处理方法
由于火箭橇轨道位置标布设方式所限制,位置标的间距仅能达到米级,针对高精度的导航卫星差分系统和惯导的性能考核,位移的分辨率远远不足,需要利用火箭橇通过每个位置标处的位置和时间信息,通过数据处理,解算出火箭橇通过相邻两个位置标之间的运动方程参数,可以得到任意时刻火箭橇的运行位置,利用时间量的统一,才能提供精确有效的制导系统比对数据。由于火箭橇在高速运行过程中,火箭发动机推力和橇体所受气动阻力、摩擦阻力不断变化,给弹道运动方程参数的解算带来了较大的难度,需要对其数据处理方法重点进行研究,这也是研究解决火箭橇时空位置测试的关键技术之一。
火箭橇轨道在一定距离内近似为空间直线,因此,本文介绍的几种时空位置数据处理算法均是基于直线运动方程。
设:从发射点开始,轨道位置标依次标记:W1、W2、W3、…、Wn-1、Wn、Wn+1、…;对应位置标之间的间距:S1、S2、S3、…、Sn-1、Sn、Sn+1、…;火箭橇通过相邻两个位置标的运行时间间隔:T1、T2、T3、…、Tn-1、Tn、Tn+1、…。位置标间距Sn和火箭橇通过位置标之间的时间间隔Tn,是经过精确测量得到的已知量。
以下介绍3种计算方法,对火箭橇在两相邻位置标之间的运动方程参数进行解算。
算法1:平均速度法
平均速度法是火箭橇运行弹道特征点速度测量中常用的一种简易计算方法。
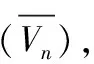
(1)
则加速度(an)为
(2)
则位置标处的速度(Vn)为
(3)
算法2:三段加加速度迭代法
考虑火箭发动机推力和火箭橇阻力在运行过程中不断变化,会引起加速度的变化,将加加速度纳入到弹道计算,是在项目研究之初提出的一种数据处理方法。
该方法是假设火箭橇在相邻三段位置标之间的运动为匀变加速直线运动,rn为该段的加加速度,则火箭橇通过任意相邻段位置标Wn、Wn+1、Wn+2、Wn+3之间的运动方程可以表示为
其中:
Sn′=Sn;Sn+1′=Sn+Sn+1;Sn+2′=Sn+Sn+1+Sn+2
Tn′=Tn;Tn+1′=Tn+Tn+1;Tn+2′=Tn+Tn+1+Tn+2
采用Matlab软件编程求解方程组,可以得到每一个位置标处的速度、加速度和加加速度值。

算法3:两段加速度迭代法
在项目研究过程中对算法1、算法2进行比较分析之后,发现算法2计算过程复杂,相较算法1,不仅没有提高精度,反之却放大了测量误差。由此,研究人员又提出一种相对简便、精度更高的两段加速度迭代算法。
依旧假设火箭橇在相邻两段位置标之间的运动为匀变速直线运动,则火箭橇通过任意相邻段位置标Wn-1、Wn、Wn+1的运动方程可以表示为
解方程组可以得到:
(4)
利用式(4)计算的速度,可以解算得到每一段加速度:
an=(Vn+1-Vn)/Tn
(5)
再利用得到的加速度和位置标间距、时间间隔量值,采用式(6),对位置标处的速度进行段内闭合平差修正计算,以提高每一段位移方程的计算精度。
Vn=Sn/Tn-an·Tn/2
(6)
4 火箭橇位移方程
火箭橇位移方程是基于时空位置测试结果和位置标段内运动弹道参数数据共同形成的。
1)采用算法1和算法3的数据处理结果,火箭橇在相邻两个位置标(Wn,Wn+1)之间任意时刻的位移内插计算方法见式(7):
(7)
式中:ΔSn为内插计算点与位置标Wn之间的位移量;ΔTn为内插计算点与位置标Wn之间的运行时间。
2)采用算法2的数据处理结果,火箭橇在相邻两个位置标(Wn,Wn+1)之间任意时刻的位移内插计算方法见式(8):
(8)
3)以发射点为起点,则火箭橇全程任意时刻的位移方程可以用式(9)表征。
Sn=Sum(S0,…,Sn)+ΔSn
(9)
式中:S0为火箭橇发射点光电组件激光轴与第一个位置标之间的距离;Sum为数值和函数(下同)。
4)为了给被检测设备提供精度更高的比对数据,则应该给出任意两个特征点之间的位移量,可以消除发射点位置、特征点位置等测量系统误差。假设计算的首点位于位置标Wn后;计算的尾点位于位置标Wm后,则火箭橇在任意两时刻之间的位移方程可以用式(10)表征。
Smn=Sum(Sn+1,…,Sm)+(ΔSm-ΔSn)
(10)
5 几种数据算法的比较分析
2018年10月,利用火箭橇时空位置校准系统对搭载的一套动态差分GPS导航设备进行了考核测试,针对该发试验的时空位置测试数据,分别采用上述3种算法进行数据处理,并计算10组有效位移数据偏差的平均值和标准偏差,数据统计比较验证情况见表1。

表1 某项目试验3种数据处理算法的结果比较
从表1不同算法处理结果的对比分析可以得出:算法1加速度波动较大;算法2处理结果误差明显增大,加速度被放大,而且算法复杂;算法3的“两段加速度迭代法”较前两种算法,计算精度都有所提升,加速度波动较小。
6 动态试验验证结果
在上述试验中,按照GPS的UTC整秒时间,采用“两段加速度迭代法”处理得到火箭橇的运动方程参数,并用式(7)对火箭橇时空位置数据进行内插处理,用式(10)计算火箭橇在两时刻之间的位移量。动态差分GPS导航设备1 s的位移量,则采用其动态差分测量得到的大地坐标值(x、y、z),用式(11)进行计算。
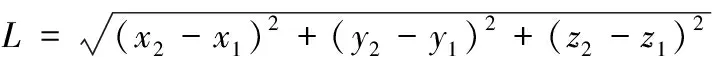
(11)
该动态差分GPS导航设备试验测试比对结果见表2。
试验结果表明:该GPS测量装置在火箭橇运行前8 s的高加速度条件下,卫星信号接收失常,导航精度较差;9 s之后低加速度条件下的导航定位性能则优于10 mm。
采用“两段加速度迭代法”处理得到的该项目试验火箭橇运行速度、加速度曲线如图2、图3。
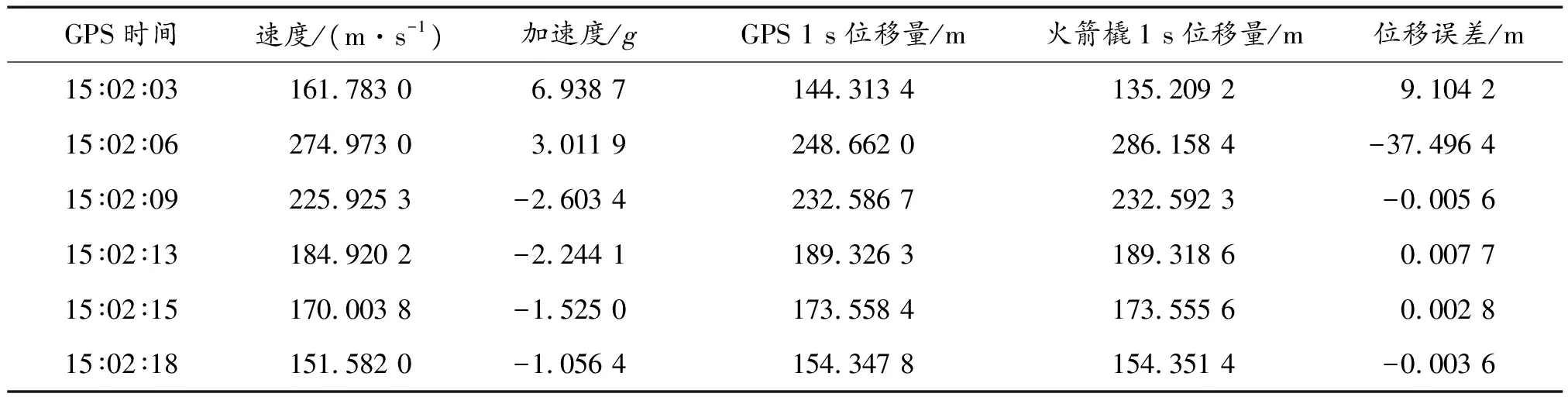
表2 某GPS产品试验测试结果部分数据
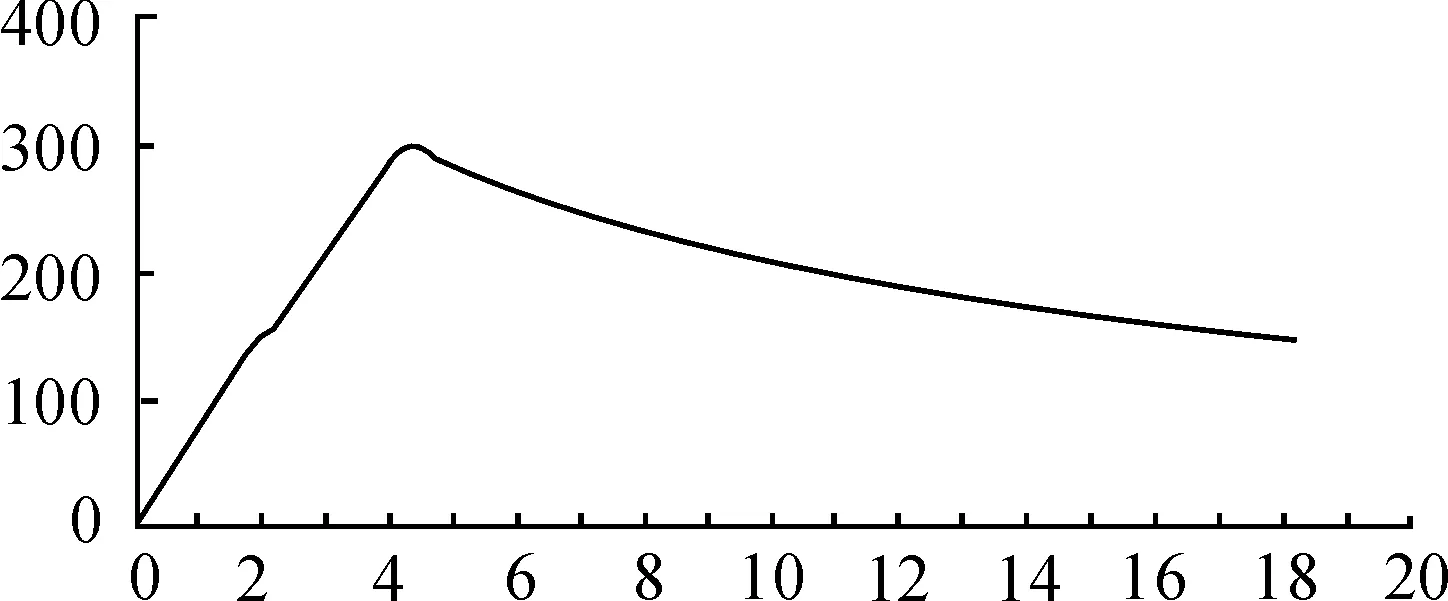
图2 某科研项目试验火箭橇时空位置速度曲线
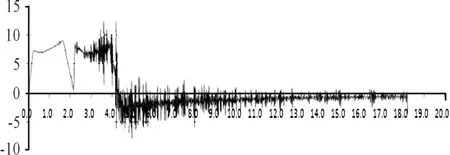
图3 某科研项目试验火箭橇时空位置加速度曲线
7 结论
本文对3种火箭橇时空位置测试数据的数据处理算法进行了分析比较,并通过实际的试验测试数据验证,采用“两段加速度迭代法”计算时空位置弹道方程参数,算法简单,得到的位置标之间段内位移方程参数闭合,航向加速度没有明显的放大趋势,数据处理误差满足需求,可以作为优选的时空位置数据计算方法,有效提升了火箭橇时空位置数据处理的精度。
