某型喷管真空羽流流场数值仿真计算研究
2019-12-03赵芃沛
赵芃沛,朱 镭
(陕西空天动力研究院有限公司,西安 710103)
火箭发动机喷管羽流特征对于发动机推力大小、红外辐射特性[1-3]以及噪声特性都有直接影响[4-6]。地面条件下羽流流动可以用连续介质模型来描述,用速度、密度、压力、温度以及位置和时间等宏观量建立流场信息的联系。真空羽流场与地面羽流场差别较大。燃气从喷管喷出后,在近似真空的环境中无干扰地迅速膨胀,呈球状扩散,扩散区域大大增加,密度急剧下降,流动状态也经历了从连续流区至过渡流区,最终到达自由分子流区的过程。此过程将经历连续流、过渡流、稀薄流等流动状态,并伴随非平衡化学反应和多种激波产生等,使羽流流动状态的描述以及相关问题的研究变得极为复杂[7-9]。
目前关于真空条件下喷管羽流主要采用DSMC[7]方法和DSMC/CFD混合方法,但目前并没有成熟的商业软件采用这两种方法来计算羽流,考虑到本文最终关注的是羽流外边界辐射特性对部件的影响,考虑时间和经费成本投入,论文采用了CFD方法来进行计算,可以快速得到初步特性来进行定性分析,在一定范围内可作为设计的初步参考。
1 计算模型与方法
1.1 计算方法和校验
本文采用的控制方程为雷诺平均N-S方程(RANS),该方程的矢量形式为:
流体粘性系数由Sutherland公式确定:
式中:μ0=1.716×10-5NS/m2,T0=121.56 K,μt为湍流粘性系数,由湍流计算模型给出。
湍流模型采用Menter的SSTk-ω模型,其流动方程如下:
式中:Gk表示湍流的动能,Gω为ω方程,Γk和Γω分别代表k与ω的有效扩散项,Yk和Yω分别代表k与ω的发散项。Dω代表正交发散项。Sk和Sω用户自定义。
采用标准壁面函数法,标准壁面函数法假定:壁面附近粘性底层以外的地区,量纲速度服从对数率分布。
流场求解利用有限体积法离散,定常雷诺平均N-S方程,各方程联立耦合隐式求解,对流项为二阶迎风格式,粘性项采用二阶中心差分格式,其他为一阶迎风格式。计算结束条件为所有残差下降3个数量级且不再变化、关键截面流量不再变化表示计算结果收敛。
采用以上模型针对文献[10]中数据进行了校验计算。该文献采用DSMC方法对真空羽流进行了数值模拟。将该方法给出的数据与本文采用CFD方法的结果进行了对比,如图1。
可以看出,在喷管内DSMC方法与CFD方法吻合度较好,因为这一区域满足连续性假设;而在距离喷管出口较远的位置,即过渡流区以外以及倒流区的区域有一定的差别。
1.2 几何模型和计算区域
计算区域和喷管几何构型如图2所示。左下角为喷管所在位置。在近似真空的环境条件下,壁面附近的气流将绕过唇口向管壁上游流动,产生倒流现象,因此将计算域水平方向和竖直方向均设定为2 000 mm。对壁面进行加密,并且对喷管出口处对流向方向进行适当加密。由于结构网格局部加密会导致整体加密的特点,故对远场的节点分布律进行调整,改为均匀分布,这样既保证喷管处网格质量,又保证远场网格均匀分布。总网格数量11万。
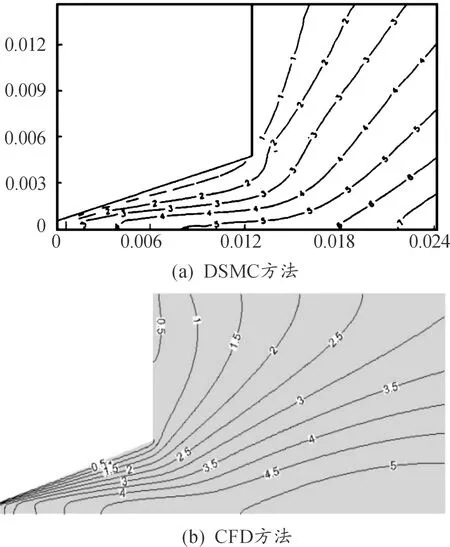
图1 Ma数等值线图
其中发动机喷管出口直径36.3 mm,喉部直径4.525 mm,出口直径36.3 mm,几何尺寸如图2所示。室压1.8 MPa,工作在120 km高度。由于120 km高度处已接近真空状态,分子平均自由程已经接近或者很有可能超过喷管的几何尺寸,因此要特别注意非连续效应的影响。
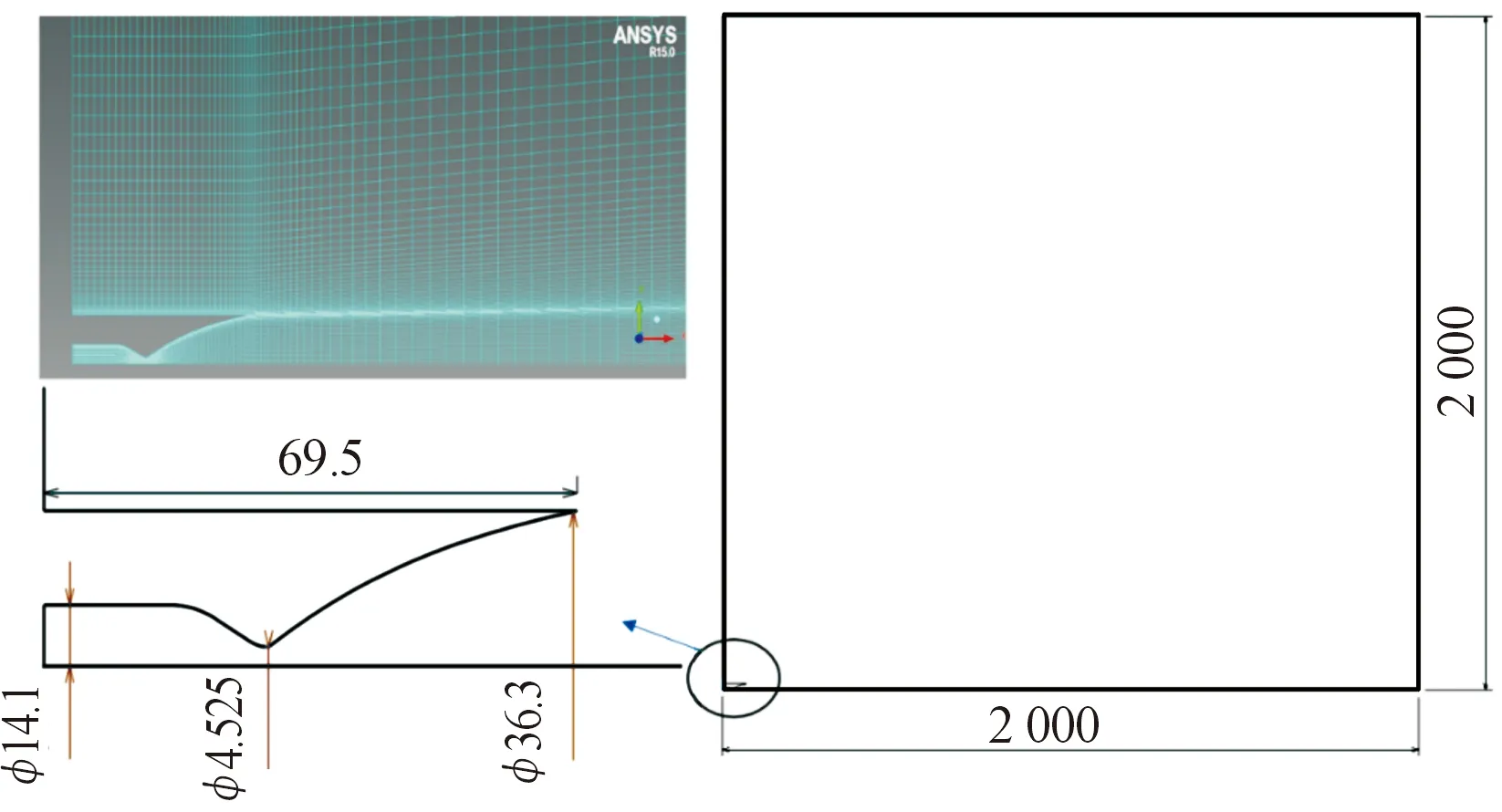
图2 计算区域和喷管几何构型
由于该喷管为轴对称喷管,主要研究羽流状态,并且计算中并未涉及到其他部件,因此整个计算域可以采用轴对称构型以减小计算量。
其中燃烧室采用质量流率入口,给定流率、总温、总压、组份;远场为压力出口,给定压力和组份;壁面均为无滑移壁面。
1.3 计算工况
表1给出了计算工况下推进剂的流量,燃料为CH6N2;氧化剂为N2O4。
在室压为1.8 MPa条件下,根据室压及燃料混合比,可以计算燃温、燃烧产物等。采用平衡流假设,经过热力学计算软件CEA计算得到:燃烧室总温3 103.7 K。以此作为计算的初始条件之一。
工作高度120 km情况下,经过查表得到:大气压力:0.002 54 Pa;温度:360 K。
由于带化学反应的计算需要耗费大量的计算资源,为了简化计算,本次计算直接给定燃烧产物,而不考虑反应过程。
经过CEA软件计算,反应主要涉及的产物有11种,分别为CO、CO2、H、HO2、H2、H2O、NO、N2、O、OH、O2。出于简化计算的考虑,选取质量分数大于1%的组份,并对这些组份浓度进行归一化处理,如表2。

表2 燃烧室组份浓度
3 计算结果
经过迭代计算,各项残差变化趋于平稳,可以认为计算结果收敛。若仅从图3所示的求解结果看,可以发现,气体经喷管加速以后流出,在低压条件下迅速扩张,达到了很高的Ma数。
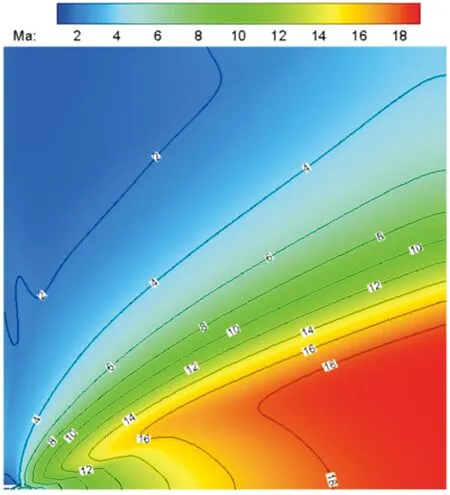
图3 Ma数等值线图
由图4、图5可以看到,相对于常压条件,真空条件下尾流扩张角度更大,呈现出弓形扩张区域。同时,由于真空条件下极低的压力,导致了垂直于流向方向上较大的扩散。可以看到,整个计算域的总温均较高,这与常压条件下完全不同。
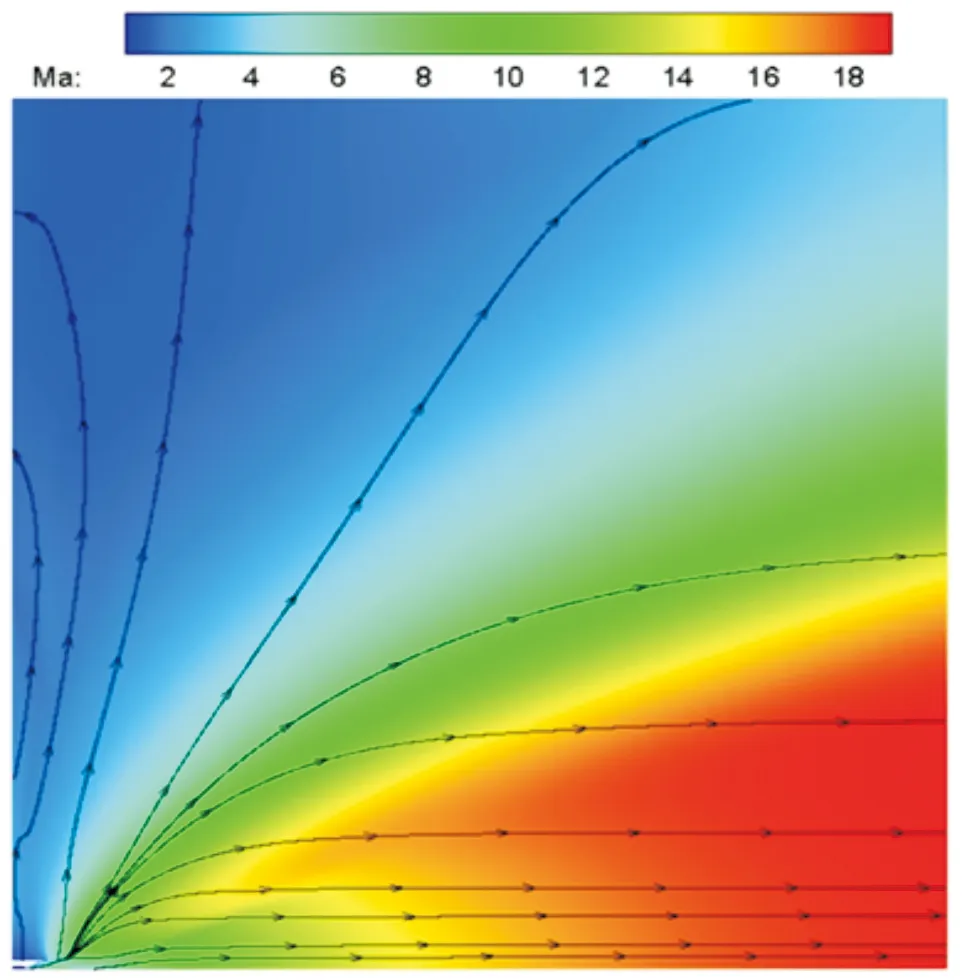
图4 整体流线图

图5 总温分布等值线图
图6、图7是喷管局部的Ma数、温度分布云图。可以看出在喷管出口形成较弱的斜激波,但波系结构和常压条件下相比较少。
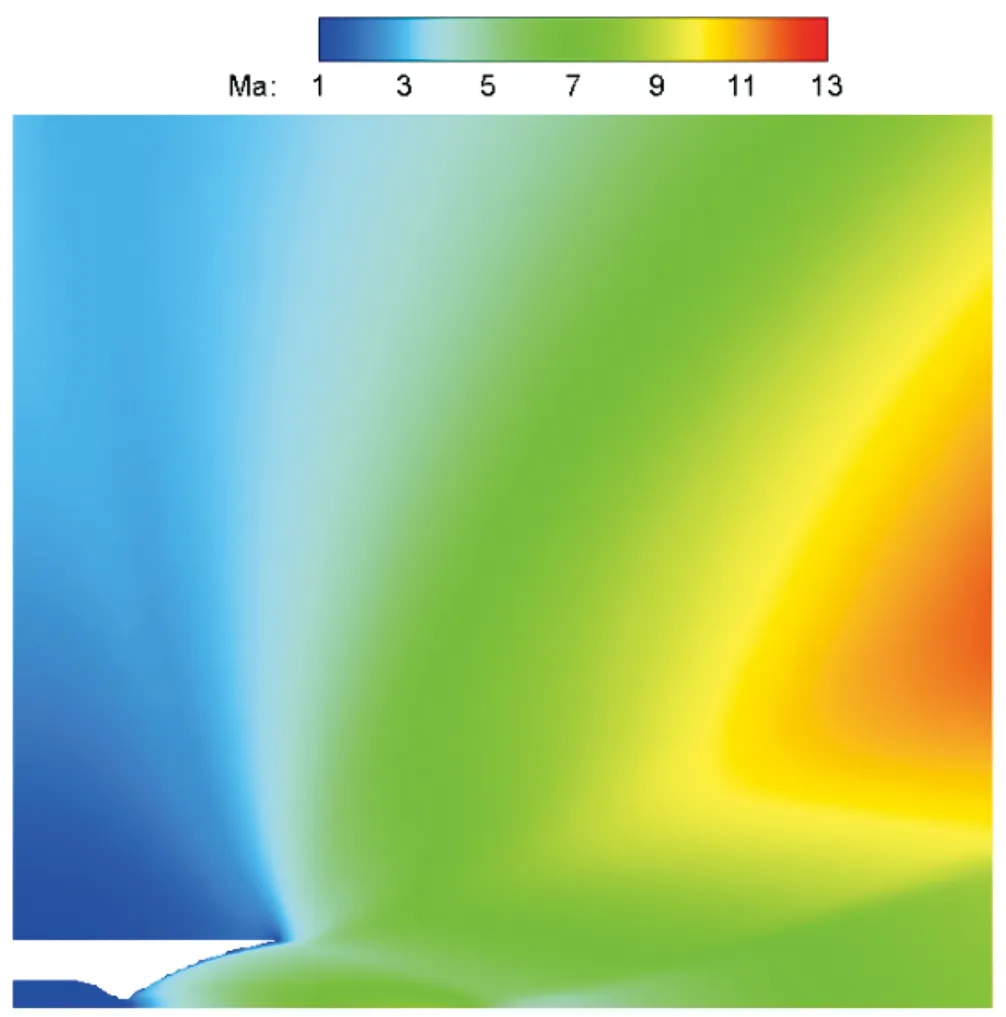
图6 喷管附近Ma数云图
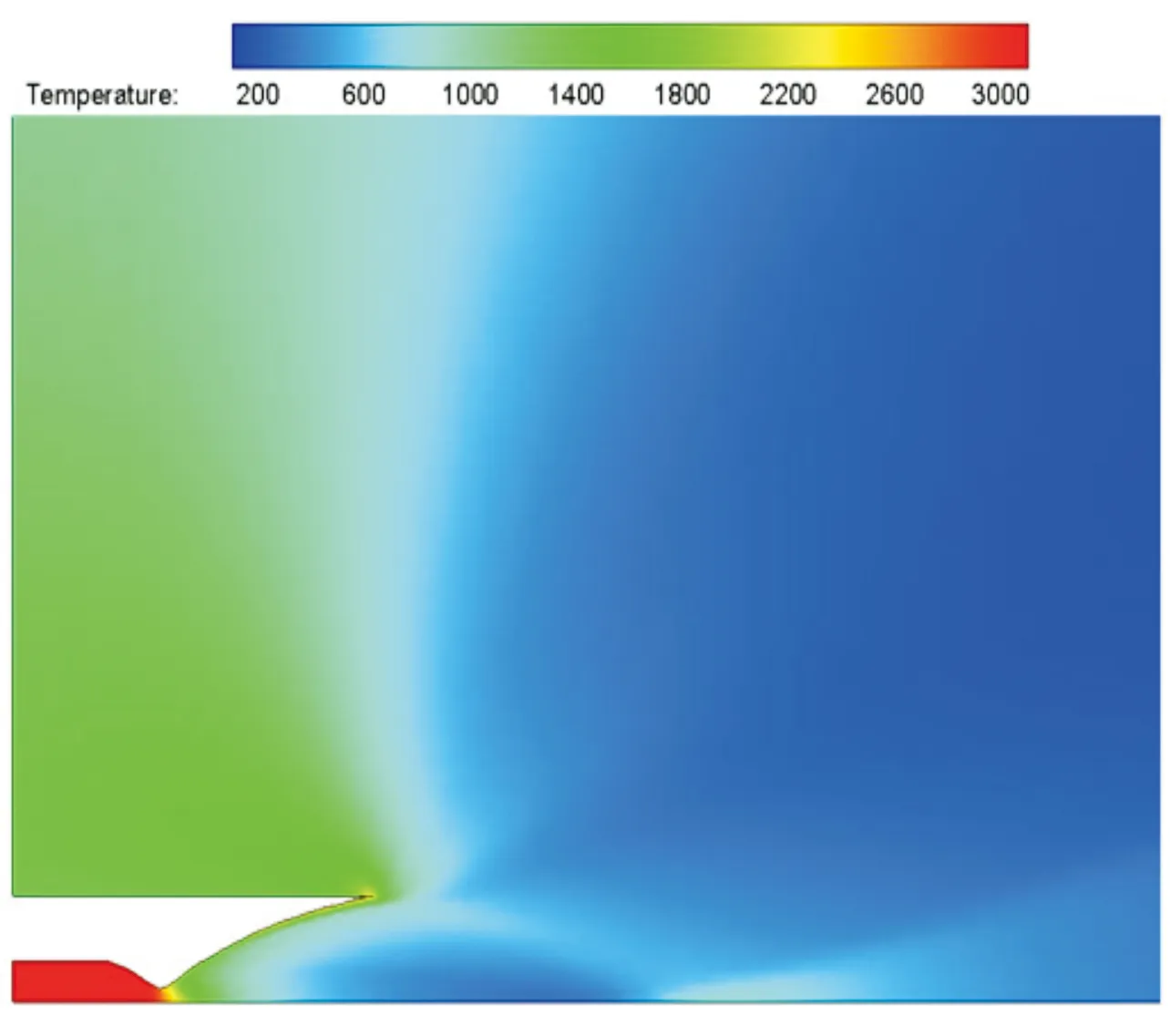
图7 喷管附近温度云图
由于喷管附近的区域(不包括水平壁面上方的倒流区)分子数目较多,符合连续性假设,因此可以认为对该区域的求解结果真实度较高。而过渡流区以外的区域需要进一步探讨。
4 结论
运用CFD方法来进行计算真空条件下拉伐尔喷管产生的羽流外边界辐射特性对部件影响,可以得出真空条件下尾流扩张角度更大,呈现出弓形扩张区域。同时,由于真空条件下极低的压力,导致了垂直于流向方向上较大的扩散。整个计算域的总温均较高,这与常压条件下完全不同。在喷管出口形成较弱的斜激波,波系结构和常压条件下相比较少。
由于喷管附近的区域(不包括水平壁面上方的倒流区)分子数目较多,符合连续性假设,可以认为对该区域的求解结果真实度较高。
