基于拓扑优化和尺寸优化的水下耐压球壳轻量化设计

高 原，黄进浩，王永军，李 飞

(中国船舶科学研究中心，江苏 无锡 214082)

0 引 言

随着经济社会的发展和科技的进步，人们对海洋资源的重视和依赖程度逐渐加深，对高性能的深海载人潜水器的需求也越来越迫切。水下耐压结构作为潜水器的核心部分，其结构性能对潜水器有着重要影响。实际上，大深度载人舱往往采用开孔球壳的形式，较大的开孔（如出入舱口）对球壳的强度和刚度影响较大，需要对其进行加强。

常见的球壳开孔加强形式为围壁加强，壳板加强，以及围壁、嵌入厚板组合加强[1]，如图1所示。这些加强形式由设计人员依据工程经验设计获得，在围壁与球壳，厚板与球壳的交接处容易产生应力集中，对球壳的安全性能造成很大影响。因此，在满足相关设计规范的要求下对耐压球壳的加强结构进行优化设计，实现球壳的轻量化，提高球壳的承载能力，降低局部应力集中是一个急需解决的问题。

目前，对于水下耐压结构的优化研究主要集中在对球壳的尺寸优化。操安喜[2]采用响应面近似模型和遗传算法对深海载人潜水器耐压球壳进行了多目标优化设计，得到了一种球壳的优化设计方案。刘峰等[3]针对开孔球壳的稳健性进行了优化研究。在这些方法当中，主要是通过分析比较在已有拓扑构型下不同参数尺寸所对应结构性能的优劣，但由于受到传统构型和已有设计经验的限制，在优化设计方面并没有太大突破。

图1 耐压球壳的典型开孔加强形式Fig.1 Typical opening reinforcement form of pressure ball shell

为了获得轻量化率更高，性能更优的耐压球壳开孔加强结构，需要研究新的理论设计方法。拓扑优化能获得结构的拓扑形式，是概念设计阶段结构新构型设计的有效方法。目前，拓扑优化已广泛应用于航空航天，车辆工程，建筑等领域，取得了很好的效果，但是对于水下耐压结构的拓扑优化则很少有人研究，因此，本文将从拓扑优化的角度对水下耐压球壳的开孔加强结构进行研究，为水下耐压结构设计提供一种新思路。

1 拓扑优化设计模型

结构拓扑优化的基本思想是把寻求结构的最优拓扑问题转换为在给定的设计域内寻求材料的最优分布问题。对于连续体结构的拓扑优化方法主要有均匀法，变密度法，水平集法等。变密度法[4-7]的基本思想是人为引进一种假想的密度可变材料，以每个单元的密度为设计变量，密度的取值范围为0到1，密度为0时，表示该单元无材料，应当删去（形成孔洞），密度为1时，表示该单元有材料，应当保留。从而将结构拓扑优化问题转化为单元材料最优分布设计问题。与其他方法相比，变密度法的优势在于适应任意形状的设计域，这对于拓扑优化在实际工程中的应用十分重要。因此，本文采用变密度方法，构造了考虑应力约束和体积约束的耐压球壳开孔加强结构的拓扑优化模型，并利用相关优化算法进行求解。

连续体结构的拓扑优化通常构造为给定材料体积的最小柔顺性问题，即

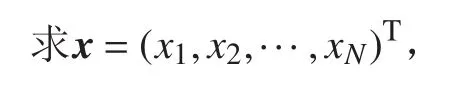
2 拓扑优化模型的求解

本文借助Optistruct软件采用MMA法求解拓扑优化问题（1）。MMA法[8-11]适用于目标函数复杂且具有多约束的拓扑优化问题。通过引入移动渐进线，将隐式的优化问题转化为一系列显式的更为简单的严格凸的近似子优化问题。在每一步迭代中，通过求解近似的子问题来获得新的设计变量。在实现MMA算法时，需要引入人工变量，以改善子问题的性态，确保可以获得可行解。优化问题（1）的数学模型表示如下：

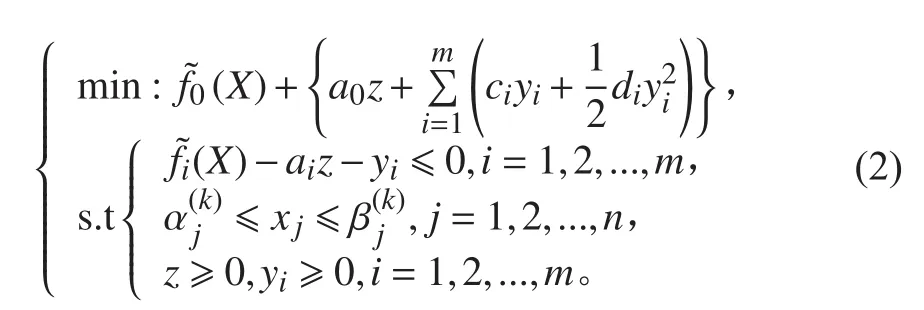
其中：

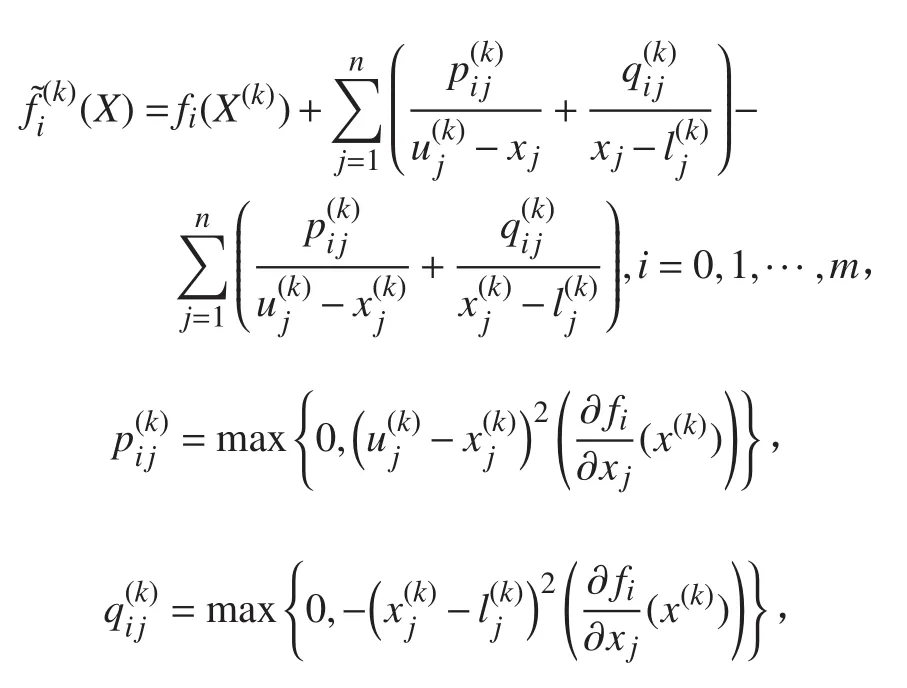
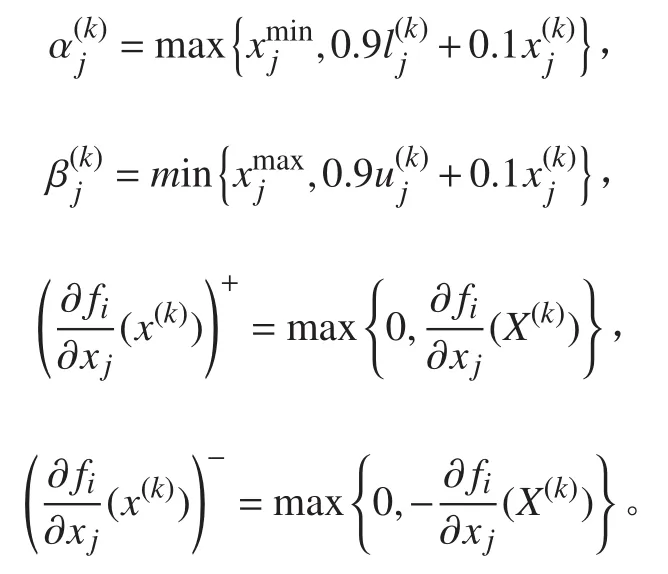
按照上述方法求解拓扑优化模型（2），即可得到耐压球壳开孔加强结构处的材料分布。但是，由于拓扑优化结构仍然存在着中间密度单元，无法获得轮廓清晰，外形规则的拓扑构型，从而无法在实际中加工制造。针对这一问题，采用拓扑优化、尺寸优化联合进行的方式进行优化设计，已确定最终球壳加强结构的构型。优化流程如图2所示。

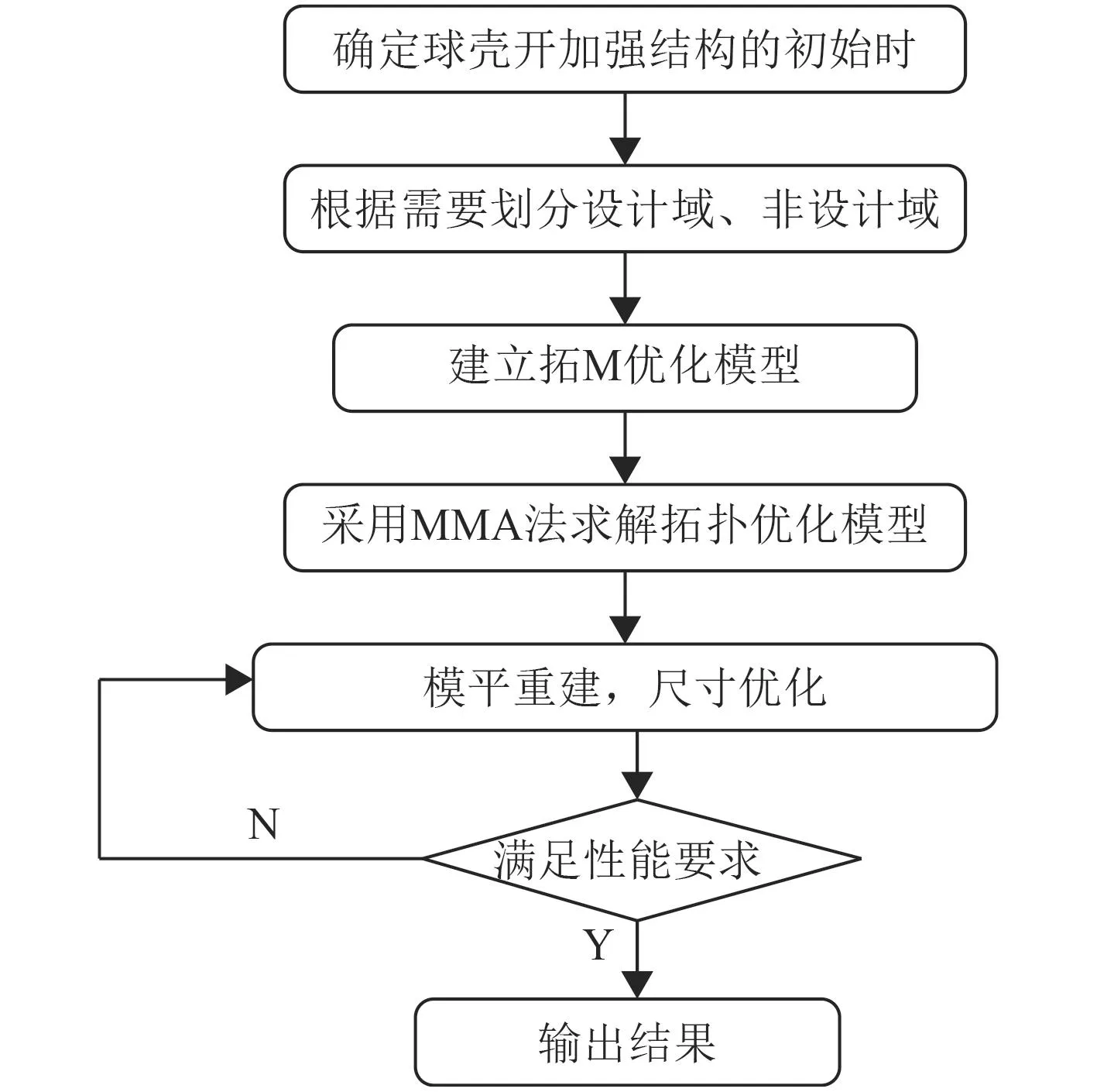
图2 优化方法流程图Fig.2 Optimization method flow chart

3 设计实例

本文以国产4 500 m耐压球壳为研究对象，球壳开孔的初始加强结构采用常规的围壁加强。围壁长180 mm，宽150 mm，球壳内径为2 100 mm，开孔半径240 mm。首先对球壳划分网格，为保证网格的质量，以六面体单元为主，为了能够体现沿耐压壳体厚度方向的应力变化情况，耐压壳体沿厚度方向保证至少2层网格。设置单元的边长为28 mm，共产生36 334个单元，196 378个节点。

耐压球壳的材料为钛合金TC4ELI，密度为4.5×103kg/m3，杨氏模量为1.1×105MPa，泊松比为0.34，屈服强度为795 MPa。

施加载荷时，外伸围壁和球壳表面受到垂直于表面的压力，压力大小取为最大工作压力46 MPa，外伸围壁开口上方施加利用压力等效原则计算得到的等效压力，大小为74.04 MPa。在计算中，壳体需要3点支持，约束6个位移分量，边界条件对称设置，这样既可以消除整个刚体位移又不妨碍相对变形，即在壳体位于轴和坐标轴上的位置取3个节点，坐标轴上的节点1和节点2，，坐标轴上的节点3，，如图3所示。

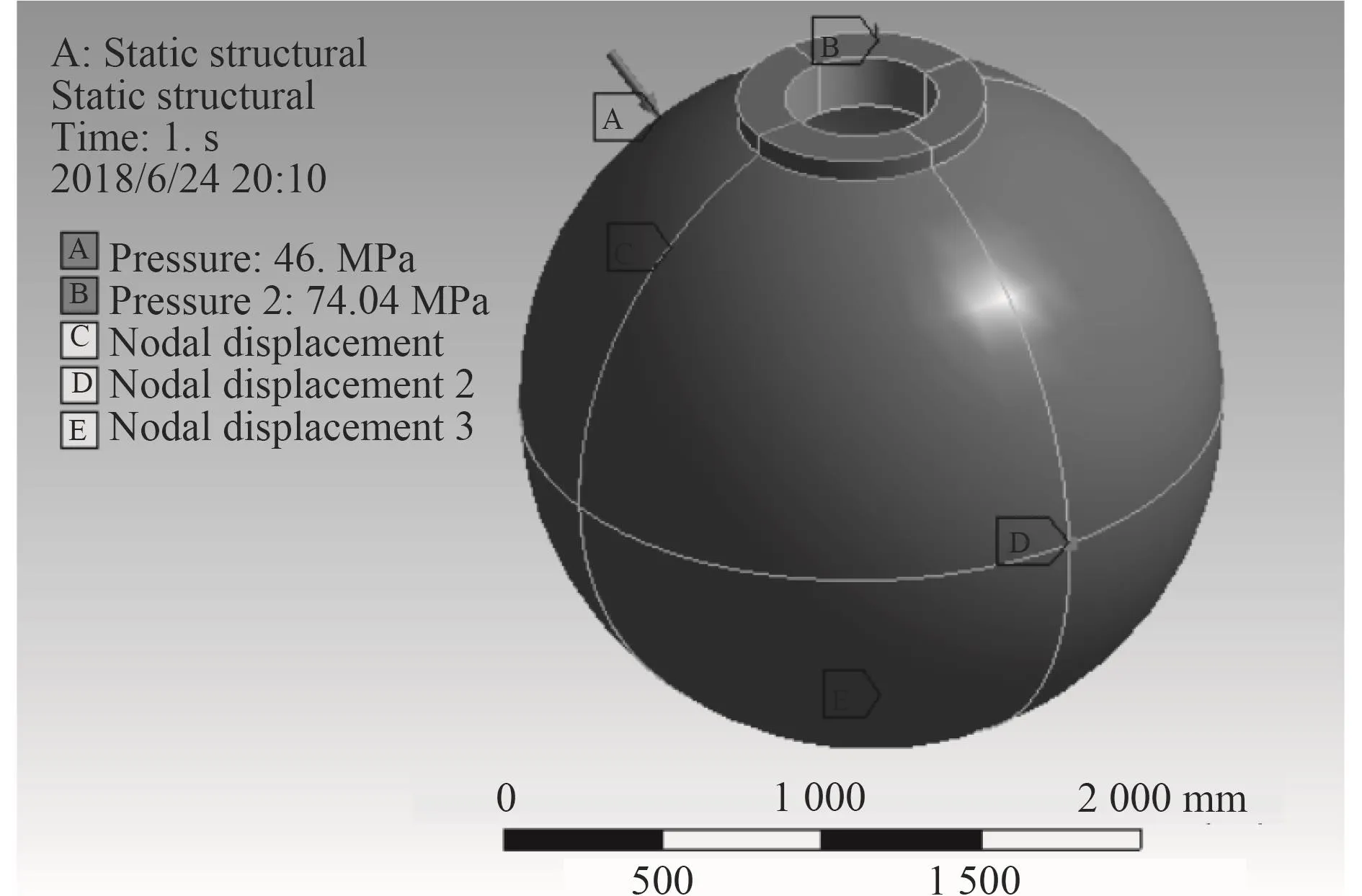
图3 对耐压球壳施加的载荷及边界条件Fig.3 The load and boundary conditions applied to the pressure ball shell

3.1 初始结构的静力分析

对耐压球壳进行静力学分析，分析结果如图4和表1所示。由图4可知，球壳的等效应力和周向应力的极值点都分布在围壁开口处，其中，最大峰值应力为732.24 MPa，略低于TC4ELI的屈服强度，同时，在围壁与球壳的交接处存在应力集中现象。分别在围壁，球壳，以及围壁球壳的连接处设置路径，得到各个位置的平均膜应力，与规范[2]的相关要求进行比较，校核结果如表1所示。

3.2 耐压球壳的拓扑优化

本文利用Hyperworks Optistruct软件对球壳进行拓扑优化。其中，球壳部分为非设计域，开孔围壁部分为设计域。为了获得最优的开孔加强形式，需要有足够大的设计空间，因此适当增大围壁的厚度，另一方面，考虑到开孔围壁的内侧需要安装舱口盖，同时，避免在优化过程中围壁出现孔洞而使优化结果不可用，需要选择围壁内侧的一层单元设置为非设计域。如图5所示，浅色区域为设计域，深色区域为非设计域。

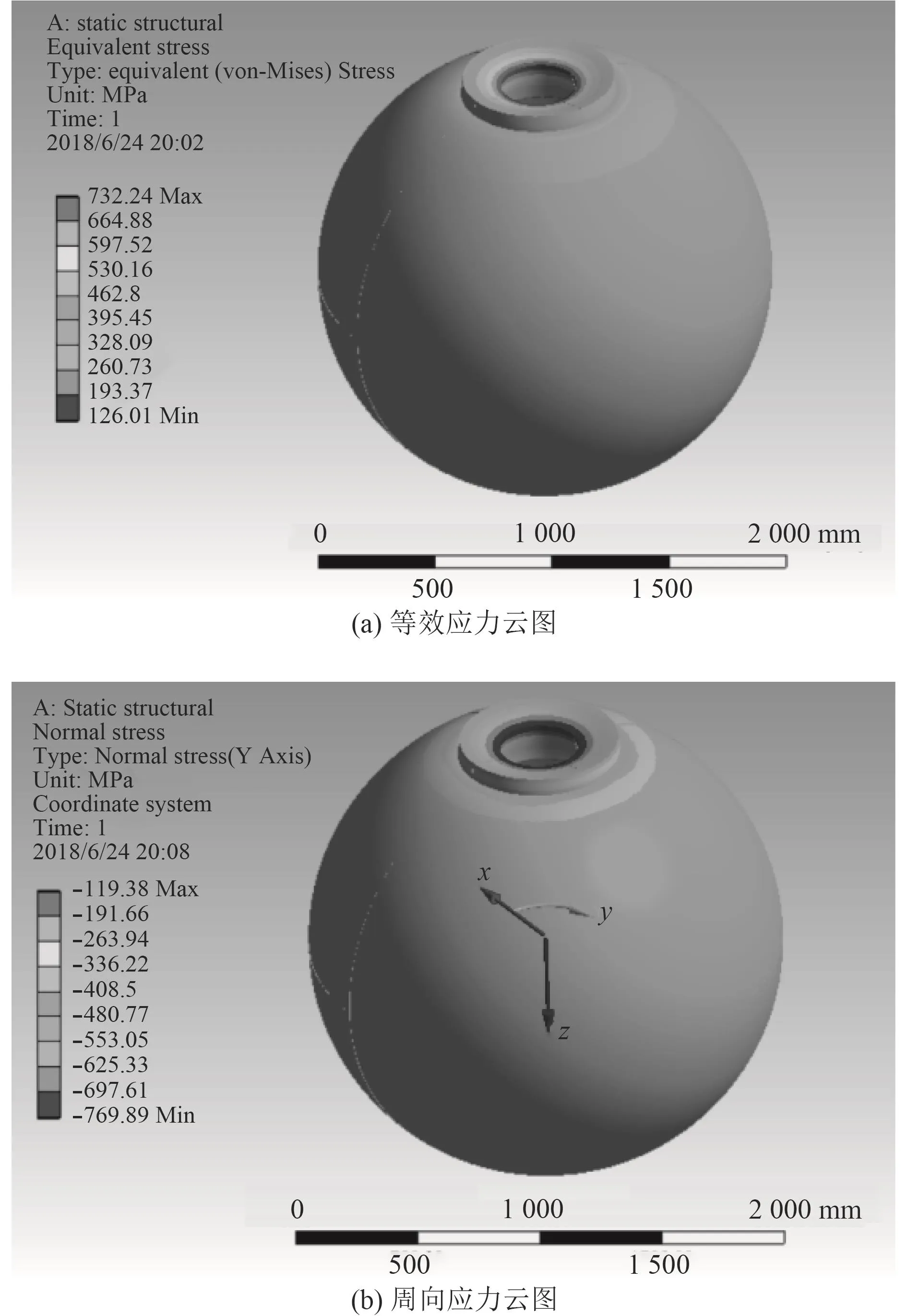
图4 原始模型静力分析结果Fig.4 Original model static analysis results

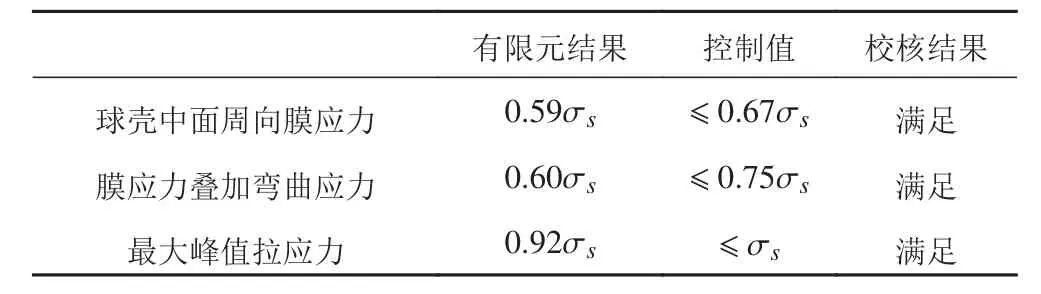
表1 球壳强度校核表Tab.1 Spherical shell strength checklist

图5 拓扑优化模型的设计域与非设计域Fig.5 Design domain and non-design domain of topology optimization model

在拓扑优化的过程中，将柔度最小定义为目标；以拓扑优化结果相对于初始设计空间的体积分数作为约束，选择多个值作为体积分数的上限，分别进行计算以确定合适的体积分数约束。控制球壳的峰值应力不超过795 MPa，最小尺寸约束不小于40 mm。启动Optistruct对耐压球壳进行拓扑优化，经过13次的循环迭代，得到了拓扑优化后的结果，如图6所示。图7为目标函数（柔度）的迭代曲线，可以看到前5步迭代下降较快，从6步起到第13步球壳的柔度大小基本保持不变。结构的柔度从减小到，减小了12.7%，说明优化后的结构刚度有了较大提升。图6为优化后的单元密度云图，设置单元密度阀值为0.3，故密度小于0.3的单元都被删去，显示了球壳的最优材料分布。将球壳的拓扑优化结果与我国自行设计的4 500 m耐压球壳进行比较，可以发现球壳的开孔加强形式非常相似，从而证明了拓扑优化结果的可行性。

图6 拓扑优化结果Fig.6 Topology optimization result

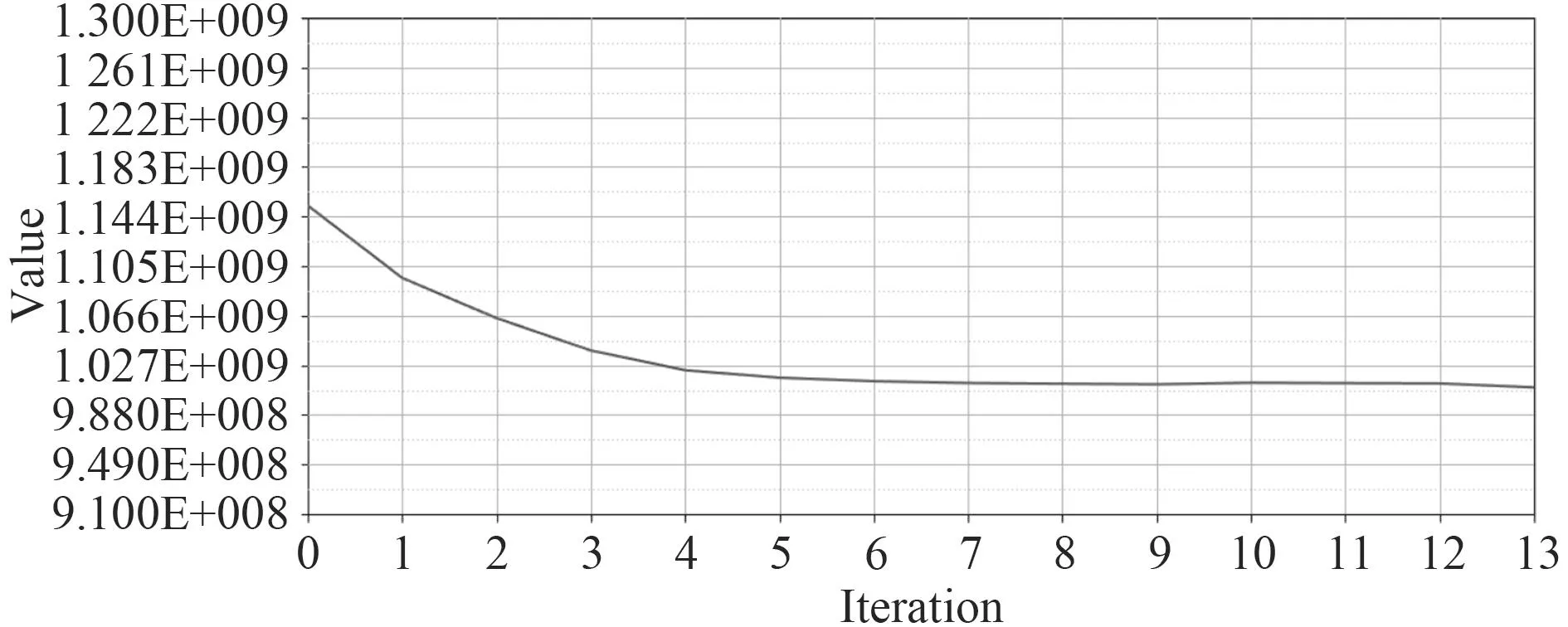
图7 目标函数（柔度）迭代曲线Fig.7 Iteration curve of the Objective function(flexibility)

3.3 开孔加强结构的尺寸优化

通过拓扑优化可以得到球壳开孔加强结构的最佳拓扑构型为锥台截面，但是要想应用到实际工程当中，需要对拓扑构型进行尺寸优化，以确定最终的结构设计。

本文利用Ansys Workbench中的响应面优化模块对球壳的开孔加强结构进行尺寸优化。如图8所示。以锥台上沿的厚度X1和斜边的角度X2为设计变量，其中，X1的取值范围为，X2的取值范围为。设置完设计变量后，分别计算围壁的膜应力，膜应力叠加弯曲应力以及等效应力。约束条件分别为：膜应力小于，膜应力叠加弯曲应力小于，峰值等效应力小于。目标函数为耐压球壳质量最小。

在Workbench中，采用试验分析的方法，选取30个样本点分别计算以确定合适的尺寸。计算结束后，软件会根据用户的需求选出候选点，并用五角星的个数表示结构的优劣。如图9所示。

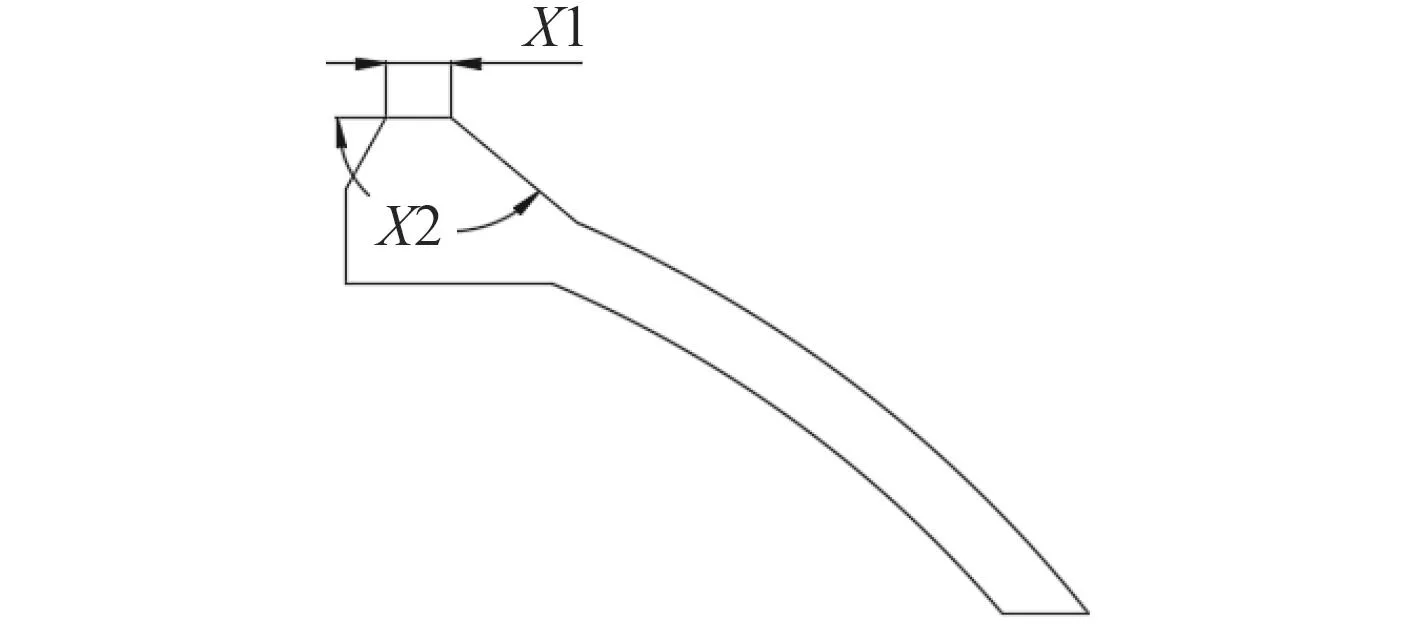
图8 尺寸优化设计变量Fig.8 Design variable of the size optimization

图9 尺寸优化Fig.9 Size optimization

从图9可以得到不同的设计变量参数组合下的球壳质量和应力值。其中，球壳的质量相差不大，而球壳的等效应力值远小于规范要求的上限，因此考虑根据膜应力的大小从候选点中选择最终的设计参数组合。锥台上沿边长为28 mm，斜面与上沿的夹角为130°。和初始结构相比，优化后的加强结构峰值等效应力下降了15.96%，重量减轻了99.1 kg。

4 结 语

本文论述了一种关于耐压球壳开孔加强结构的优化设计方法，即联合使用拓扑优化和尺寸优化方法，可以得到最优开孔加强结构的材料分布。算例表明，通过拓扑优化可以得到最优开孔加强结构的合理形式，通过尺寸优化，可以得到最优开孔加强结构的合理尺度。优化后的加强结构较传统的加强结构在应力强度和重量两方面都得到了显著改善，满足规范的相关要求，实现了结构轻量化的目的，提高了耐压球壳的承载能力。该方法为设计人员优化水下结构提供了新的思路和途径。