欧洲足球五大联赛进球的时间序列模型构建及预测

全涛

0 前言

足球在《运动训练学》项群训练理论中属于技能主导类同场对抗性运动项目，其评定方法属于命中类项目[1]，进球的结果直接影响着比赛成绩的好坏[2]。在现代足球的发展历史上，欧洲足球五大联赛代表世界足坛的顶尖水平，引领世界足球运动的发展方向。进球的特征和规律，从一定程度上体现职业联赛足球技战术打法体系的形成与革新，同时反映国家地区的足球水平和民族精神的文化特色。

近些年，统计学方法在足球相关研究中的运用逐渐增多，从简单的计量统计，到卡方检验、t检验，再到复杂的回归分析、因子分析[3]。时间序列分析是数理统计中的一个重要分支，主要通过随机过程理论和数理统计方法来揭示数据的特点和规律，构建不同的模型和未来预测，以解决社会生活中的实际问题。通过中国知网关于“时间序列分析”的计量可视化分析结果表明：（1）发文量在近20年出现逐年递增的趋势，并在近10年保持稳定的状态；（2）主题分布在时间序列、数学模型、ARIMA模型、实证分析、小波分析等；（3）学科分类主要集中在数量经济、数学、金融、计算机、地球物理、测绘、环境、临床医学、公共卫生与预防医学、国民经济、控制工程、大气、交通运输、区域经济与农业经济上。总之，时间序列分析已经广泛运用于各个领域，吴怀宇认为它在经济领域的研究和应用一直很活跃，并扩展到社会、气象、水利、交通、信息、农业、工业、教育等领域[4]。张美英和何杰强调时间序列的研究在理论及应用中都取得了极其丰硕的成果，但还有待于完善其理论及开辟新的应用领域，对于实际数据来说，没有最好的模型，只有最适合的模型，新时间序列模型的建立仍然是今后学者要继续研究的问题[5]。在体育方面，张小龙从理论的角度讨论了其可行性，通过实例分析进一步证实了在体育中应用时间序列分析的优越性[6]；任波和戴俊通过时间序列计量分析我国城乡居民消费支出与体育产业发展的互动关系[7]；辛驰和赵雪晴通过SAS和E-view对NBA球员林书豪进行了实例分析，建立时间序列模型并定量评价[8]；陈颇等人先后运用了时间序列分析方法，研究中国体育事业财政投入与经济增长的关系[9-10]。总之，时间序列分析具有足球赛事数据研究的可行性，既可以通过数据直观分析其特点，又可以丰富足球运动训练理论体系。

本文按照时间序列分析的方法对欧洲足球五大联赛进行多项赛事的模型构建与趋势预测，客观探索高水平足球比赛进球的特点和规律。

1 研究对象与方法

1.1 研究对象

欧洲足球五大联赛2000—2001赛季至2016—2017赛季的场均进球。

1.2 研究方法

1.2.1 文献资料法

通过电子资源数据库查阅了有关时间序列分析、足球比赛进球分析的论文30余篇，阅读学习了《时间序列数据分析》《世界优秀统计工具SPSS-高级篇》《应用统计学》相关教程与学术著作[11-15]，并在足球数据库网站上查找了关于欧洲足球五大联赛进球的数据统计与评论文章。

1.2.2 数理统计法

通过500彩票网[16]和足球之夜数据库[17]收集了欧洲足球五大联赛2000—2001赛季至2016—2017赛季共17年的年场均进球数据，并逐一核对，确定原始数据库。利用SPSS22.0软件在计算机上对数据进行了时间序列分析，构建欧洲五大联赛的进球ARIMA模型并预测。

1.2.3 对比分析法

在数理统计的基础上，利用比较分析、逻辑归纳等对欧洲五大联赛的进球特征进行分析。

2 研究结果

2.1 数据集的预处理

首先把数据录入到SPSS中（见图1），共有1个字符串型“赛季”、5个数值型“进球”变量，其中数值保留两位小数。

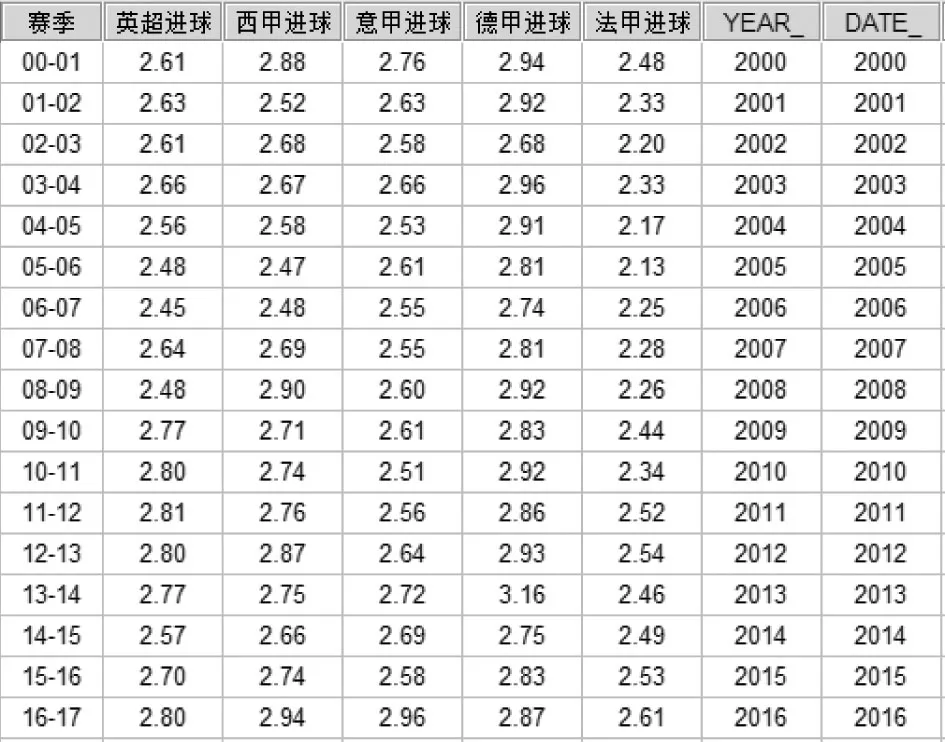
图1 欧洲五大联赛进球数据集（2000/2001—2016/2017）Figure 1 Goal Data of the Big Five European Football Leagues(2000/2001-2016/2017)

由于欧洲足球五大联赛受到地中海气候或海洋性气候的影响，赛制实行跨年度举行，如“2001—2002赛季意大利足球甲级联赛”这一称谓，因此软件系统或者分析中的“2000年”等同于“2000—2001赛季”，其他依次类推。

2.1.1 离群点的检验

离群点是指一个时间序列中，远离序列一般水平的极端大值和极端小值。而形成离群点的系统外部干扰是多种多样的，可能是采样中的误差，也可能是被研究现象本身由于受各种偶然非正常的因素影响而引起的[18]。为此，运用SPSS对五大联赛17个赛季的场均进球进行了探索性分析，用箱图检验离群点，以便提高构建模型的准确性（图2）。

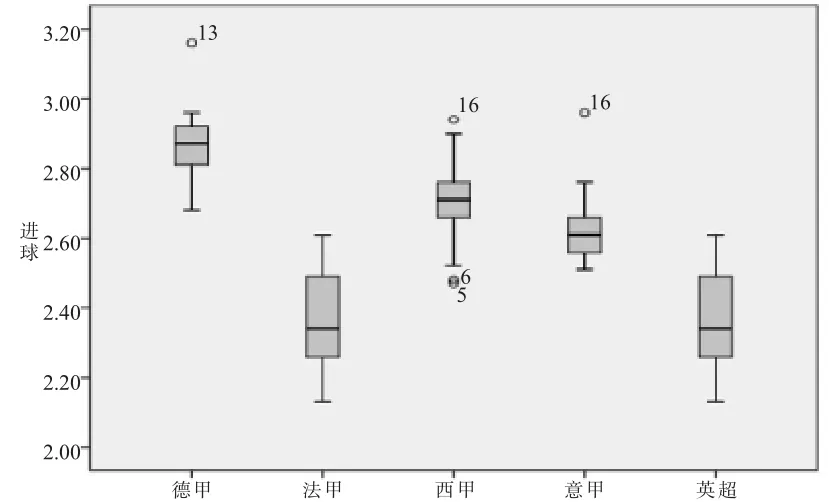
图2 进球数据箱图Figure 2 Goal Data Boxplot

从图2可以看出，法甲、英超不存在离群点，德甲、西甲、意甲存在离群点现象。由图1数据对应后得到：德甲 2013年数值 3.16，西甲 2005、2006年数值2.47、2.48和 2016年数值 2.94，意甲 2016年数值2.96，共计5个数值存在不同程度的离群。

2.1.2 平稳性的判定

时间序列分析的前提条件是数据必须具有平稳性特征，在统计学上可以运用序列图观察和自相关、偏相关分析图判定时间序列平稳性[19]。为判断该数据是否平稳，原始数据的序列图包含5个变量。

从图3可以看出，从2001—2002赛季开始不同程度的出现下滑现象，2005—2006赛季逐渐回升，在2009—2010赛季开始处于2～3年的平稳状态，之后随着球员转会自由市场和足球商业化的日益发展，五大联赛进球对比日益缩小。

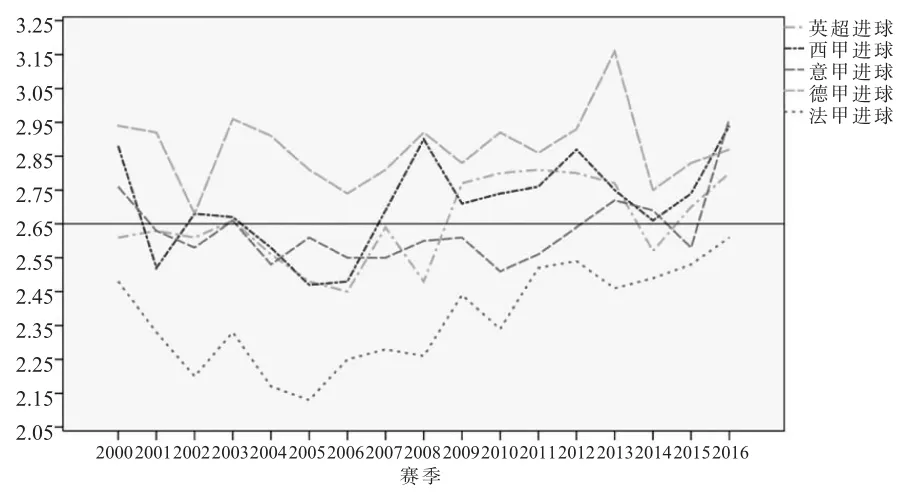
图3 欧洲足球五大联赛进球序列图Figure 3 Goal Sequence Diagram of the Big Five European Football Leagues

2.2 模型识别

2.2.1 序列图

从原始序列图（3）来看，场均进球数随着时间的推移在起初下降后逐步上升，该序列线性特征明显。现对五大联赛的原始数据进行1阶差分，序列图（4）围绕均线上下波动，状态基本平稳，差分效果良好。

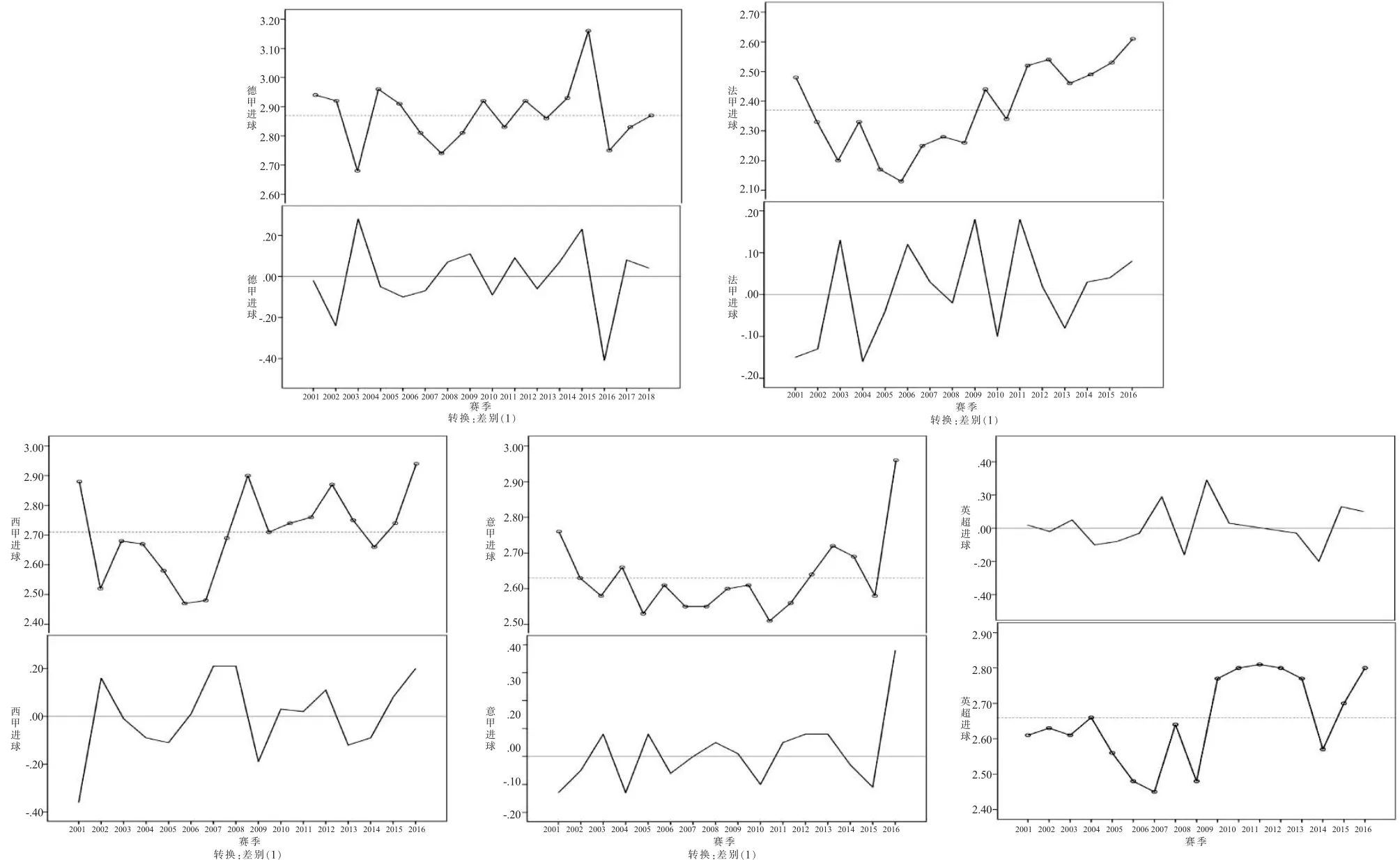
图4 欧洲足球五大联赛原始数据与1阶差分序列对比图Figure 4 Comparison of the Raw Data and 1st Order Difference Sequence in the Big Five European Football Leagues

2.2.2 自相关与偏自相关分析

为了更好地把握五大联赛进球特点，通过自相关系数（ACF）、偏自相关系数（PACF）分析图进一步识别模型和目标序列定阶。运用SPSS对数据进行了自相关分析，输出结果如图5。

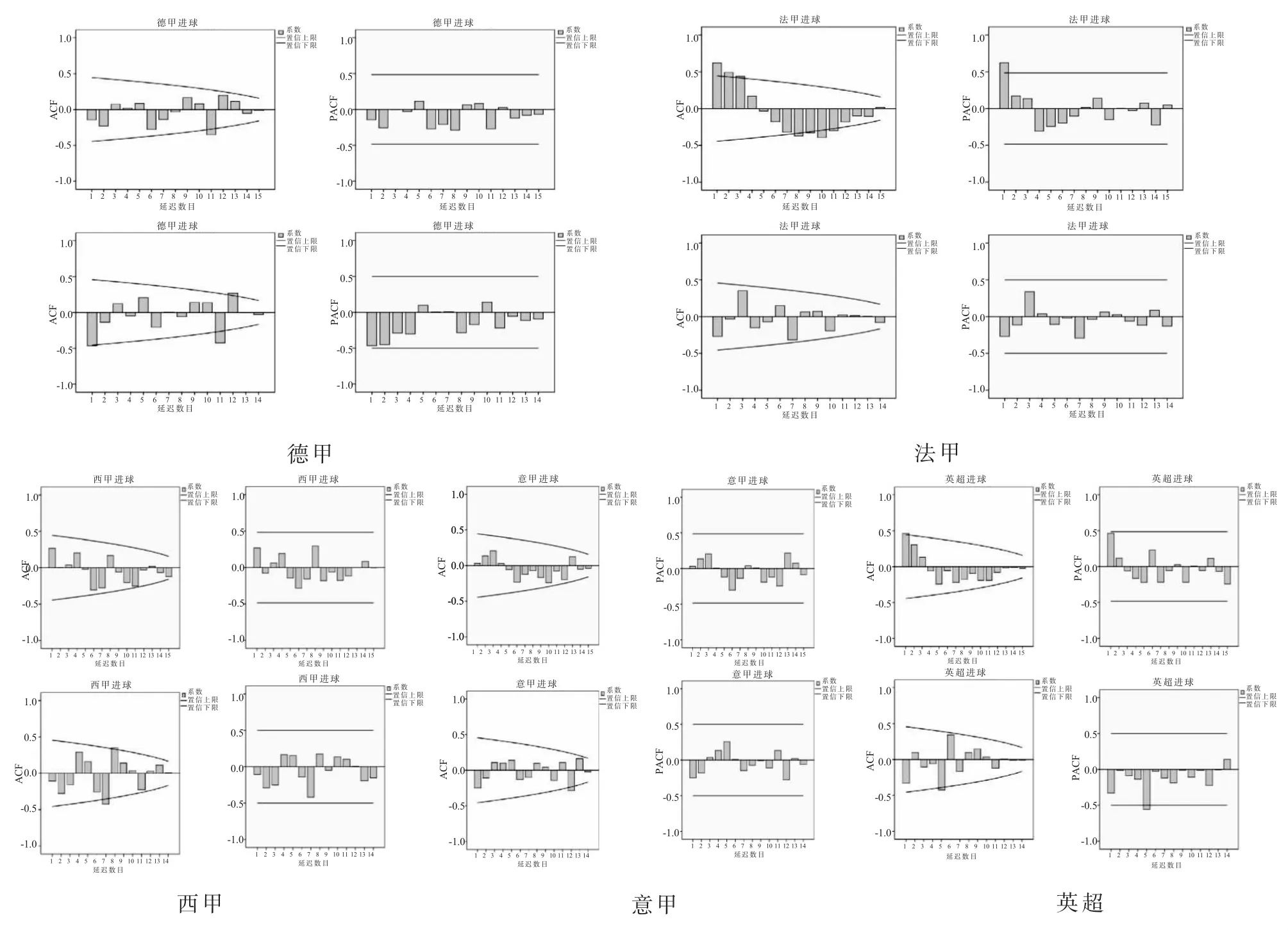
图5 欧洲足球五大联赛进球自相关与偏自相关分析图（0,1）Figure5 Analysis of Autocorrelation and Partial Autocorrelation of Goals in the Big Five European Football Leagues(0,1)

总体上随着延迟数目的增加，自相关系数并没有显著的趋近于0，且有近一半数值落在了置信区间之外，同时，偏自相关系数也逐渐减弱，说明该时间序列并非平稳。为了更好确认数据的平稳性，对原始数据进行1阶差分处理，得到自相关系数、偏自相关系数大多数进入置信区间。

2.2.3 假设检验

假设 H0：原始时间序列 Xi平稳，H1：序列 Xi不平稳；采用显著性格水平α=0.05进行检验。从表1来看，原始数据P＜0.01，具有很强的显著性差异，则拒绝H0假设接受H1假设，证明该数列不平稳；进行1阶差分后，P＞0.05，相反则接受H0假设判定该数列为平稳序列，且数值逐渐增大总体态势为上升，与序列图的分析一致。

这里只列出法国足球联赛自相关和偏相关函数的Box-Ljung统计量情况，其他联赛可以采用类似的方法确定其初步模型。

2.2.4 p,q取值

Box-Jenkins方法是根据时间序列模型ACF和PACF图的识别规则，建立相应的ARIMA模型[20]。序列ACF、PACF性质及其与模型参数之间的关系[21]，整理如表2。

依据函数特征表的识别规则，对五大联赛ACF、PACF函数分析图进行了详细分析，统计了1阶差分后的ACF和PACF落在置信区外、内的数量，并对非常接近的特殊分布作了不确定、可能认定，用来初步识别模型，分布和模型情况。

由表3得到初步模型，其中德甲为ARIMA（0,1,3）或 ARIMA（2,1,3），法甲为 ARIMA（0,1,0）或ARIMA （0,1,1），西 甲 为 ARIMA（1,1,2）或 ARIMA（1,1,3），意甲为 ARIMA（0,1,1）或 ARIMA（0,1,2），英超为 ARIMA（1,1,1）或 ARIMA（1,1,2）。 值得注意的是，在这个过程中，充分考虑了离群点（值）的影响，运用加权的方法将特定的时间点作为离群值来建模。

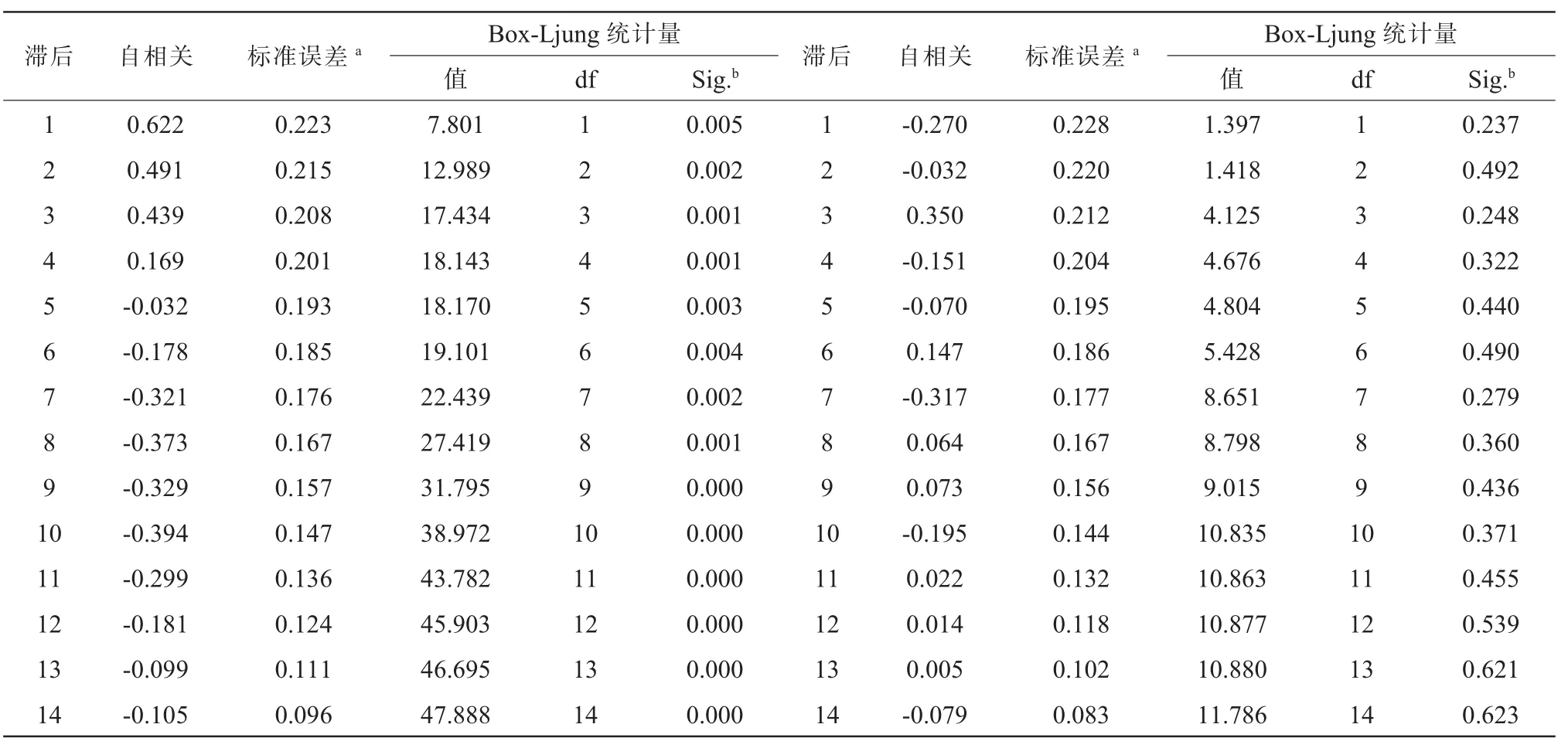
表1 法甲进球自相关和偏相关函数对比表（原始与1阶差分）TableⅠComparison of the Autocorrelation and Partial Correlation Functions of the French Armor Goals(Raw and 1st Order Difference)

表2 零均值平稳序列的自相关函数和偏自相关函数特征表Table II Characteristics of Autocorrelation Function and Partial Autocorrelation Function of Zero-mean Stationary Series

表3 欧洲五大联赛进球ACF、PACF分布和p,d,q取值一览表（1阶）Table III List of ACF,PACF Distribution and p,d,q Values of Goals in the Big Five European Football Leagues(1st Order)

2.3 模型构建

运用SPSS22.0软件计算，得到五大联赛的模型结果分析见表4。

2.4 模型预测

模型的适用性检验按白噪音独立性检验准则，其基本思想是：若由估计模型拟合的残差纯粹由干扰产生，则该模型是适用的，可用于外推预测；否则，估计模型不合适[22]。为此，对进球残差自相关和偏相关进行了检验，结果如图6。

通过建立ARIMA模型对欧洲足球各大联赛的均进球数据进行拟合，并对2017-2020赛季的进球数值进行了结果预测，形成模型拟合及预测图（图7）。

同时，根据命令输出了2017—2020年的预测值、UCL、LCL值详见表5，以供参考。

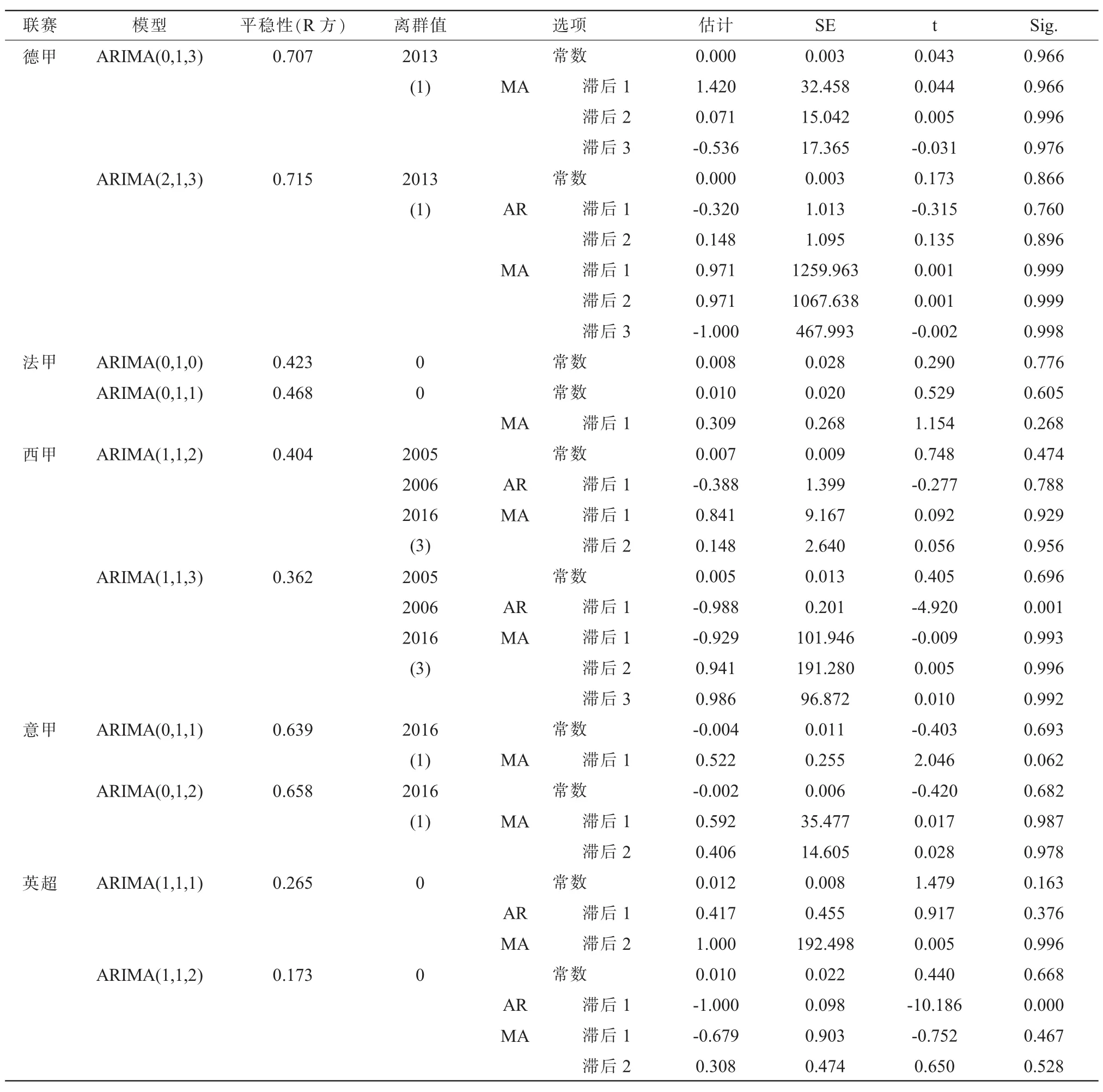
表4 欧洲足球五大联赛进球模型参数表（d=1）Table IV Goal Model Parameter Table of the Big Five European Football Leagues(d=1)

图6 欧洲足球五大联赛进球残差自相关和偏相关检验图Figure 6 Autocorrelation and Partial Correlation Test Card of Goal Scores in the Big Five European Football Leagues

图7 欧洲足球五大联赛进球模型及预测图（2017—2020）Figure 7 Predicted Value of the Goal Model of the Big Five European Football Leagues(2017-2020)

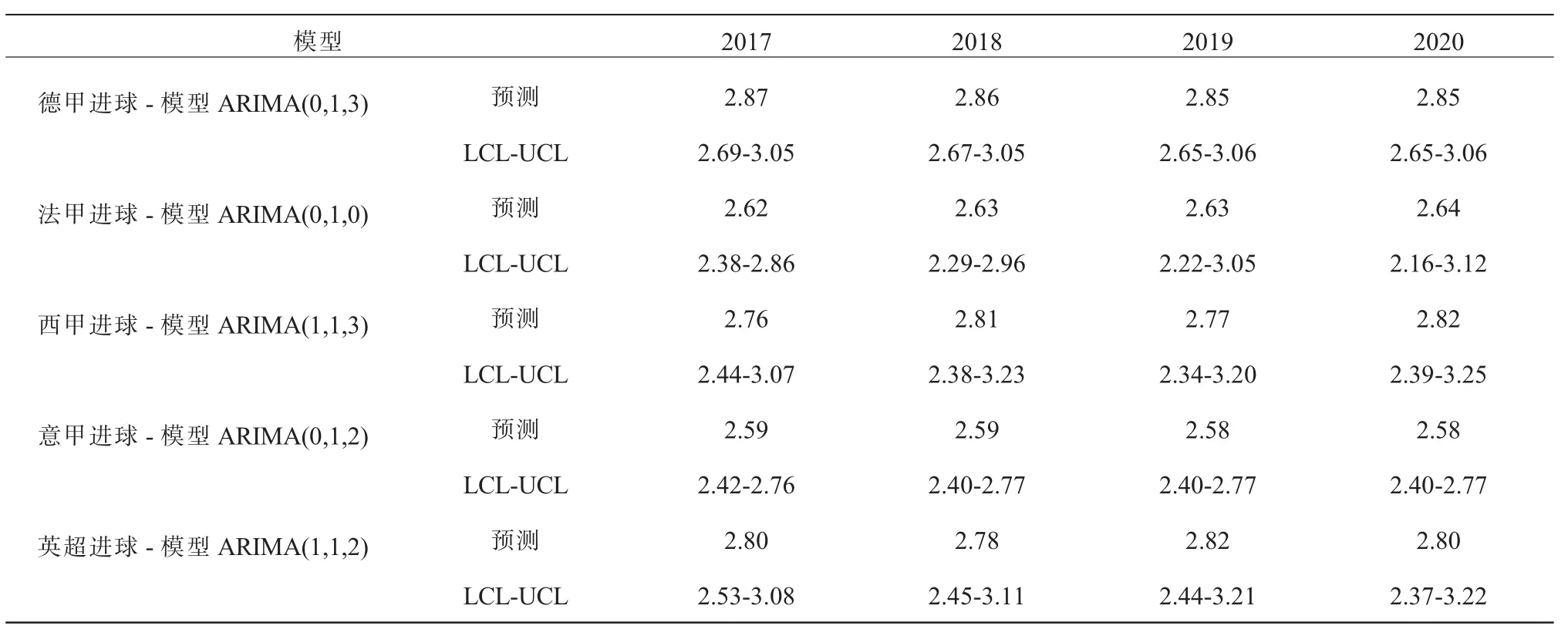
注：对于每个模型，预测都在请求的预测时间段范围内的最后一个非缺失值之后开始，在所有预测值的非缺失值都可用的最后一个时间段或请求预测时间段的结束日期（以较早者为准）结束

3 分析与讨论

3.1 欧洲足球五大联赛的进球特征

在体育运动项目的模型构建过程中，原始数据本身具有随机性，非稳定性特征比较常见，这就需要采用合适的方法进行序列分析，以保证研究结果的正确性。前期对离群点的分析和平稳性的判定非常重要，否则会直接影响模型的拟合精度，得到一些虚假的信息，对后续的时间序列分析会造成一定影响。

对“五个离群点”的进一步分析发现：德甲2013年场均3.16个进球，说明德甲保持较高的场均进球，一直是崇尚进攻的联赛。西甲2005和2006年出现的2.47、2.48两个最低的进球数值，原因在于那个时期西甲球员出现新老交替，进攻能力下降；意甲2016年的场均进球为2.96，这与意甲改变传统保守的技战术打法有关。另一方面，从进球序列图的走势来看，表现出单一赛事不同时期的波动性和不同赛事之间的横向差异性特征。五大联赛场均进球的数据随着时间的推移上下波动，并有上升的趋势。在作时间序列分析时，首先初步判断该序列的稳定性特征，如果不稳定需要对数据进行自相关函数、偏相关函数、特征根的检验，采取1阶或2阶差分处理，直至数据平稳，才能继续进行模型的识别，以期构建合理的模型和预测，探索欧洲足球五大联赛的进球特点和规律。路云亭把第五种足球描述为“盛传于世界各地且带有本民族文化传统意味的多元化的足球”[23]，笔者认为欧洲五大联赛具备不同的差异，反映着一个国家的民族精神和区域文化特色。如法甲最讲究“思想性”与“公平性”，其竞争力有待于提升；意甲受到经济的影响较大，表现出传统保守的特点；英超的商业化最为成熟，比赛更加注重身体对抗、比赛节奏较快，观赏性高；西甲联赛注重技术与进攻，具有很强的观赏性；德甲的民族特点突出，注重整体配合。

3.2 欧洲五大联赛的ARIMA模型

由于足球比赛中的场均进球序列不存在季节性周期趋势，这里的模型识别没有考虑季节问题。在模型识别时，则是通过序列图和自相关与偏相关的1阶差分处理，为的是保证数据的平稳性，使ACF和PACF进入95%的置信区间，进一步确定d=1，同时为下一步的参数估计做好准备。

在这里需借助于自相关函数（ACF）和偏自相关函数（PACF）以及其相关分析图来识别时序特性，如法甲（表1）运用BOX-JENKINS预测法假设检验，采用显著性格水平0.05进行1阶的前后对比检验，统计量由小于0.01到大于0.05，表明效果良好，证明这一方法的可行性。在确定p,q值时，需根据自相关函数（ACF）和偏自相关函数（PACF）图的拖尾、截尾两个特征，内外部的分布情况，参数之间的关系3个方面，初步建立相应的ARIMA模型。运用SPSS软件的“分析—预测—创建模型”命令，自动输出的统计量和相关信息，包括平稳的（R方）、离群值、参数估计、SE、t、Sig。 主要是通过比较平稳的 （R 方）、P值、观测值和拟合值的曲线拟合度情况，来确定各大联赛的最终进球模型。分析如下：德甲：平稳R方分别为 0.715和 0.707，P值分别为 0.966和 0.866，第一个模型的两项数值比第二模型高，所以模型定为ARIMA （0,1,3）。法甲：两个模型的常数估计值为0.008和 0.010，P值分别为 0.605和 0.776，ARIMA（0,1,0）拟合度高于 ARIMA（0,1,1），加上 R 方相差不大，取 P值为 0.776，模型确定为 ARIMA（0,1,0）。西甲：因ARIMA（0,1,2）迭代在优化期间不收敛，可能不可靠数据放弃。另两个模型的平稳R方分别为0.404和0.362，P值分别为0.474和0.696，结合模型的拟合情况确定为ARIMA （1,1,3）。同样的方法推断意甲模型为 ARIMA（0,1,2），英超模型为ARIMA（1,1,2）。

3.3 欧洲五大联赛的短期预测

通过自相关和偏相关的残差检验表明，数值都落在95%置信区间内，与0无显著差异，模型的检验效果比较好，所以残差通过白噪声检验，由此诊断模型是可行的，可用于短期预测。

从预测图（图7）左侧可以看出，进球序列上整体上成波动状态，拟合值和观测值曲线在整个区间整体上拟合情况良好，拟合值的波动非常接近实际观察值波动性。从参考线右侧预测了2017—2020赛季的场均进球态势，其中德甲趋于缓慢下降，法甲继续稳步上升，西甲处于上下波动、上升趋势，意甲趋于稳定，英超则呈上下波动、下降趋势。当然，这只是单纯数据的预测，不排除有其他特殊因素的影响，在前期“进球数量稳定特征”[24]的研究结论有所论述，即在常态下，场均进球应该是一个比较平稳的状态，不会有很大的波动，当然不排除特殊情境（争冠、降级、出线等）的影响。总之，由于足球运动是攻守平衡的一项同场对抗项目，进球总体上应该趋于稳定状态，介于 2.5～3.0之间。

4 研究结论

4.1足球在 《运动训练》学具有技能和命中的双重属性，决定了进球是多种技战术相互作用的结果，在现有足球规则倡导进攻的条件下，场均进球较少，有稳定增加的态势，这符合足球竞技体育项目的发展规律。

4.2欧洲五大联赛的进球特征表现出单一赛事不同时期的波动性和不同赛事之间的横向差异性。波动性主要是随着时间的推移上下波动，并有上升的趋势；差异性反映不同国家的民族精神和区域文化特色，从进球曲线表现上，依次为：德甲、西甲、英超、意甲、法甲。

4.3在建模的过程中，要充分考虑离群值、数据平稳性问题，严格按照时间序列分析的相关分析、假设检验、p与q取值等步骤建模。欧洲五大联赛的模型是德甲为 ARIMA（0,1,3），法甲为 ARIMA（0,1,0），西甲为 ARIMA（1,1,3），意甲为 ARIMA（0,1,2），英超为 ARIMA（1,1,2）。

4.4通过模型的构建可用于短期预测，进球序列上整体上成波动状态，拟合值和观测值曲线在整个区间整体上拟合情况良好。