均匀正方薄板转动惯量的计算

摘 要：转动惯量是刚体力学中的一个十分重要的概念。本文将用微元法与标度变换法计算均匀正方薄板过质心的定轴转动惯量，类似可以拓展到一般的立方体的计算中。期望此文方法能够给学习大学物理的读者以有益的启发。

关键词：转动惯量;微元法;标度变换法

刚体定轴转动的转动惯量是大学物理刚体力学部分的重要概念，对于其计算也是必须掌握的重要内容。一般的大学物理教材中对均匀直棒、圆柱、圆盘（环）、球体的转动惯量的计算较多，而对均匀正方薄板的转动惯量的计算很少。本文将主要运用微元法、标度变换法计算其绕质心轴的转动惯量，包括质心轴垂直薄板位置与质心轴平行薄板位置。

一、 质心轴垂直位置的转动惯量

方法一：微元法

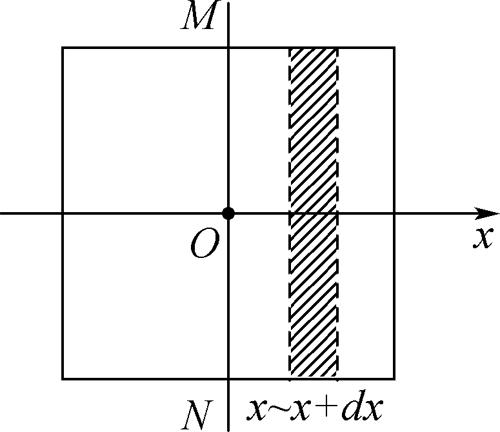
图1如图1所示为一均匀正方薄板，設质量为m，边长为l，计算过质心O点垂直于薄板的转动惯量大小。薄板的面密度表示为σ=ml2，建立坐标轴Ox，在x处取微元dx，对应的阴影部分直棒的质量为dm=σldx，利用平行轴定理，相对于0点的转动惯量可以表示为dJ=112l2dm+x2dm，对x从-l2到l2积分可得整个薄板相对于质心轴的转动惯量J=∫112l2+x2dm=∫l2-l2σll212+x2dx=16ml2。

方法二：标度变换法

图2

如图2所示，将正方薄板均分成四等份，每一份仍为正方薄板，其中一个质心为O′，可知与整个薄板相对于各自通过质心转轴具有相同的转动惯量形式，设整个薄板的相对通过O点垂直转轴的转动惯量为J=kml2，则一小份薄板相对于O′的转动惯量为J′=km4l22，由平行轴定理，相对于O的转动惯量为J′+m42l42，整个薄板的转动惯量应为四个等大的小薄板相对于0点的转动惯量之和，即J=4J′+m42l42，带入J、J′，表达式为kml2=14k+18ml2，得k=16，则整个薄板相对过质心O垂直轴的转动惯量为16ml2。

以上两种方法计算结果一致。微元法很好地利用了微积分的数学思想，对于刚刚学习高等数学的同学，很好地锻炼了运用数学知识解决实际问题的综合能力;标度变换法则是从物理量量纲的角度出发，利用图形自相似的特点，求解待定系数，从而求得转动惯量，方法新颖、独特。

二、 质心轴平行位置的转动惯量

方法一：微元法

图3

如图3所示，MN为一条平行于板边穿过质心O的转轴，计算正方薄板相对于MN的转动惯量大小。建立坐标轴Ox，在x处取微元dx，对应的阴影部分直棒的质量为dm=σldx，相对于0点的转动惯量可以表示为dJ=x2dm，对x从-l2到l2积分可以得到正方薄板相对MN轴的转动惯量大小为J=∫x2dm=∫l2-l2σlx2dx=112ml2。

方法二：标度变换法

图4

如图4所示，将均匀正方薄板用两条平行于板边穿过质心O的直线MN、PQ四等分，每小份仍为正方薄板，因此与整个薄板相对于通过质心的平行转轴的转动惯量形式相同。设整个薄板的相对通过MN转轴的转动惯量为J=kml2，则一小份薄板相对于过O′点对应的平行转轴的转动惯量为J′=km4l22，由平行轴定理，相对于O的转动惯量为J′+m4l42，整个薄板的转动惯量应为四个等大的小薄板相对于0点的转动惯量之和，即J=4J′+m4l42，带入J、J′，表达式为kml2=14k+116ml2，得k=112，则整个薄板相对过质心O垂直轴的转动惯量为112ml2。

三、 总结

利用微元法与标度变换法求解均匀正方薄板转动惯量，结合平行轴定理与垂直轴定理得出了相应的转动惯量公式。推导过程思路清晰，方法灵活。加强转动惯量部分的计算，有助于学生对大学物理学习的深入理解。

参考文献：

[1]杨小云.常见均匀刚体转动惯量的计算[J].科技教育，2018（29）：184-185.

[2]韩众.几种形状规则刚体转动惯量的计算[J].山西大同大学学报（自然科学版），2014，30（4）：25-27.

作者简介：

狄学春，山东省高密市，青岛科技大学高密校区。