对生产装置单一原料主要产品收率的线性回归分析

刘志强 王秋 任广行 金巍

摘      要：以无截距线性回归模型及SPSS软件对一生产装置单一原料的主要产品收率进行线性回归分析，通过对该装置23组投入产出数据的研究，确定了回归效果显著、稳定性良好的无截距项线性模型，得到了有代表性的单一原料的产品A、B的收率。该分析方法的正确建立，对优化装置原料结构有意义。

关  键  词：线性回归; SPSS;产品收率

中图分类号：TQ 021.9      文献标识码： A      文章编号：1671-0460（2019）10-2392-04

Abstract： The linear regression analysis of the main product yield from a single feedstock in the production plant was carried out with the non-intercept linear model and SPSS software. Through the study of 23 sets of input-output data of the device， a linear model without intercept term was established. The model had obvious regression effect and good stability， and the yields of the products A and B of single raw material were obtained. The establishment of the analytical method is of great significance to optimize the raw material structure of the plant.

Key words： Linear regression;SPSS;  Product yield

在化工生产优化操作中，建立正确的分析方法，明确各原料产品收率，对于正确评价每种原料的经济性，优化装置原料结构有着重要意义[1-3]。

以某生产装置为例，该装置主要原料可分为F1、F2、F3、F4四大类，主要产品为A、B两种，本次分析以23组该装置月投入产出数据为基础，利用无截距项正态线性模型及SPSS（Statistical Product and Service Solutions）软件[4-6]对装置单一原料的主要产品收率进行线性回归分析。

1  无截距项线性模型的建立及SPSS软件的应用

1.1  建立无截距项正态线性模型

设b1、b2、b3、b4分别为原料F1、F2、F3、F4对于产A的收率，每月四种原料投入量分别为X1、X2、X3、X4，A的产量为Y，建立无截距项四元线性模型

1.2  SPSS软件应用

1.2.1  数据来源

以该装置23个月的投入产出数据（见表1）为基础进行分析。

1.2.2  模型操作

将表1中数据在模型数据录入界面输入后，进行以下操作：

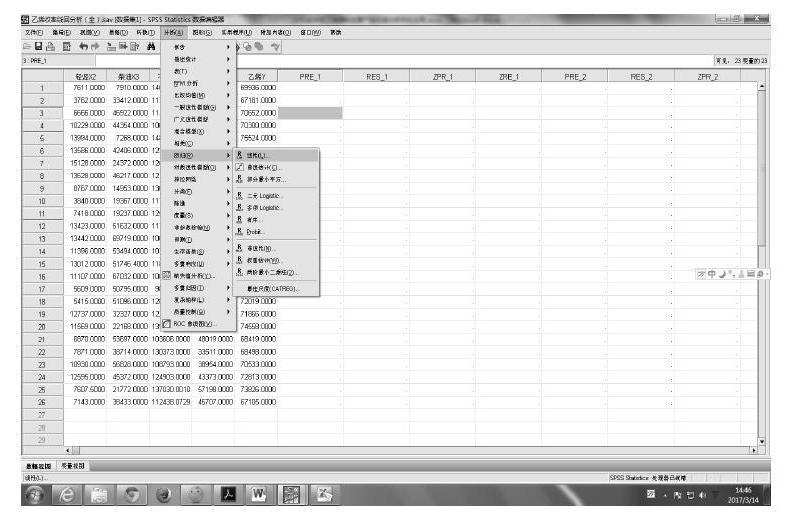
在操作菜单中选择回归、线性，点击确认。

将因变量、自变量分别选入，在方法中选择进入。

在统计量、绘制、保存选项中进行相应操作后

在选择选项中进行如下操作。

2  线性回归方程确定及显著性检验

2.1  根据模型输出结果确定回归方程

=0.326x1i+0.438x2i+0.308x3i+0.326x4i    （2）

2.2  线性回归方程显著性检验

利用方程求因变量估计值及相关差值平方（见表2）。

在表2数据基础上，可计算得到

R2=0.965、R=0.982、F=74.6、SIG=0（模型给出）

根据方程的R、R2、SIG和F得出该模型表现出显著性。

3  结果与讨论

3.1  用留一法檢验模型稳定性

留一法LOO（leave one out）交叉性验证是一种内部化的检验，这种检验过程是以所建模型的参数为自变量来进行的[7]，具体操作为逐一从全部样本中剔除1个样本然后重新建方程，用该新建方程预测剔除掉的样本，比较预测结果与统计结果得到残差，通过推倒得到交叉验证相关系数q2（q2代表模型的内部稳健程度）。

由表3可以看出，q2>0.5，说明该模型具有稳定性和可预测性，公式模型的q2=0.926，另外，该模型的R2- q2=0.039 ，该差值与所建立的模型稳定性正相关，差值越小，模型稳定性越好。

3.2  模型的残差分析

残差分析结果如表3所示，标准化残差的标准P-P图如图1所示，统计值与预测值残差频率直方图如图2所示。

由图1和图2可以看出，预测值与统计值表现出良好的线性关系，标准P-P图的对角线上分布着大多数样本。另外，模型的直方图基本符合正态分布的特点，代表了该模型被成功建立。

3.3  产品B收率的回归方程及检验值

对产品B相关的统计数据进行了同样的分析：

确定回归方程：

=0.153x1i+0.318x2i+ .138x3i+0.150 x4i   （4）

各检验值   R2= 0.846  R=0.920  F=39.3  SIG=0   q2=0.867

说明产品B收率的线性回归模型同样具有显著性和稳定性。

由图3和图4可以看出产品B收率模型的建立也是成功的。

3.4  产品A、B收率的确定

通过以上分析可得出在统计学上有意义的产品A、B的收率（见表4）

4  结 论

通过对该装置23组投入产出数据的研究，确定了回归效果显著、稳定性良好的无截距项线性模型，得到了有代表性的单一原料的产品A、B的收率。

参考文献：

[1]陈 魁.应用概率统计[M].北京：清华大学出版社，2000：20-30.

[2]同济大学数学系.线性代数[M].北京：高等教育出版社，2006：25-28.

[3]史春薇，田强，葛骞，鲁传涛.基于SPSS统计软件在多元线性回归校验数据中的应用[J].当代化工， 2014， 6.

[4]谢海宇.用线性回归技术降低汽油调合成本[J].当代化工， 2004， 4.

[5] 兰秀菊.1.8 Mt/a催化裂化装置生产方案模型的建立和优化研究[D].北京：中国石油大学（北京），2005.

[6]于战德.多元线性回归分析法在蜡油加氢产品质量控制上的应用[C].中国统计学会石油化工统计分会第四次统计学术研讨会论文集.广州分公司，2010：20-27.

[7]闫辉.1.8Mt/a催化裂化装置工艺模型的建立和生产方案优化研究[D].河北：河北工业大学，2007. DOI：10.7666/d.d042300.