基于流固耦合的T型管振动特性分析

2019-12-02俞建峰

振动与冲击 2019年22期

赵江，俞建峰，楼琦

(1. 江南大学机械工程学院，江苏无锡 214122；2. 江苏省食品先进制造装备技术重点实验室，江苏无锡 214122)

压力管道因其安全和经济的特点被广泛应用于石油、天然气、船舶和城市供水等领域。但是，在进行气体和液体输送时，由于管道中流体的间歇吸入/排出运动，可能会在管道系统中产生流量脉动和压力脉动，并导致在不连续区域(如弯头，三通管或阀门处)引起严重的管道振动[1]。异常或过度的振动会导致管道系统疲劳失效，腐蚀穿孔和其他安全问题[2]。

管道系统的振动研究主要包括理论分析[3-4]和试验研究[5-7]。Huang等[8]采用消元Galerkin方法计算直管两端的不同边界条件下的固有频率，得到了不同边界条件的流体输送管道的固有频率方程。Dai等[9]采用传递矩阵法研究了流体流动引起的组合力对直管和弯管的固有频率的影响。付永领等[10]基于流固耦合方法，研究了弯管转角对管道振动的影响，发现弯管转角减小有利于减弱管道振动。俞树荣等[11]基于ANSYS Workbench软件，分析了弯管在脉动压力下的受力变形情况，指出由于流体的附加作用力，管壁会在转角处出现最大变形。曹源等[12]采用ALE描述和罚函数耦合来模拟水锤过程中T型管的流固耦合问题，发现管壁动态周向应力峰值是静周向应力峰值的1.2～1.6倍，动态周向应力与水锤具有相同的变化周期。

目前管道流固耦合的研究对象主要集中在直管和L型弯管方面，对三通管如T型管的流固耦合振动研究相对较少。本文利用ANSYS Workbench 17.0软件对典型三通管结构-T型管进行振动特性的流固耦合模拟，旨在为管道结构设计和优化提供参考依据。

1 流固耦合数学模型

1.1 流体运动控制方程

T型管中的流动可以看作是不可压缩流动[13]，流体连续性方程和动量方程为

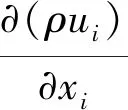
(1)

(2)

在T型管内水流存在漩涡流动，流线弯曲程度很大，这里选用RNGk-ε湍流模型[14]

(3)

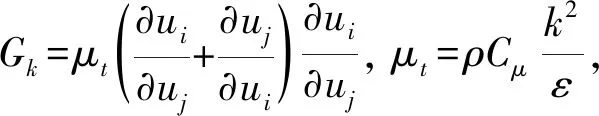
1.2 管道运动控制方程

对于具有n个自由度的管道系统，其单元运动状态下的有限元方程为[15]

(4)

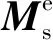
考虑管道受到流体作用，其整体的结构动力学方程为[16]

(5)

式中：Ms为管道整体质量矩阵；Cs为整体阻尼矩阵；Ks为整体刚度矩阵；δ为位移矢量；fo为流-固交界面上流体与管道相互作用的矢量；Fd为除fo外的外界激励矢量。

1.3 管道流固耦合方程

流体模型和固体模型的网格单元可以不同，但是在流固耦合面上需满足力(τ)，位移(d),热流量(q)和温度(T)等变量的守恒[17]，即满足以下4个方程

df=ds

(6)

n·τf=n·τs

(7)

qf=qs

(8)

Tf=Ts

(9)

式中：df，ds为流体和固体在流固耦合面上的位移；τf，τs为流体和固体在流固耦合面上的剪切应力；qf，qs为流体和固体在流固耦合面上的热流量；Tf，Ts为流体和固体在流固耦合面上的温度。

不考虑温度变化时，应该同时满足位移平衡方程和应力平衡方程[18]，即通过满足这两个变量守恒来实现流体与固体之间分析参数的传递。

2 管道几何模型及模态分析

2.1 几何模型

选择一段T型压力管道作为研究对象。管道中间截面剖面图见图1，管内径为100 mm，管道壁厚2 mm，AC=500 mm，BC=500 mm，BD=1 000 mm。A,B为进水口，D为出水口。

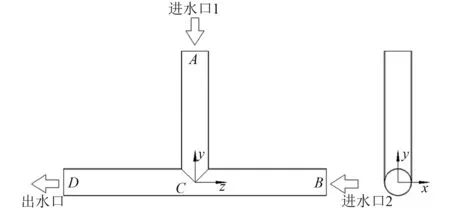
图1 管道几何结构示意图Fig.1 Schematic diagram of the pipe geometry

2.2 模态分析

利用ANSYS CFX进行管道流体动力学计算，管道几何结构见图1。湍流模型采用RNGk-ε模型，壁面采用无滑移壁面设置，计算过程不考虑热交换。分别计算不同流体压强(0 MPa，2 MPa，4 MPa，6 MPa，8 MPa)，不同分支管进口流速(5 m/s，10 m/s，15 m/s，20 m/s)，不同密度流体(水，液压油,90#汽油和液化石油气)的管道内流场情况。通过Workbench中的Transient structure模块进行瞬态结构动力学耦合计算，求解设置关键在于流固耦合面(Fluid Solid Interface)设置，ANSYS Multi-field solver负责整个耦合求解。流体计算结束后，将结果流场载荷加载到对应的管道壁面上，进行预应力模态分析。

利用ANSYS Workbench中的Static Structural和Modal模块对管道进行结构受力与模态分析。其中管道壁厚为2 mm，管道A端、B端和D端采用固定约束，管道材料采用Q345B(16Mn)材料，其主要参数为密度7 800 kg/m3, 杨氏模量2.0×105MPa，泊松比0.3。结构振动中其主要作用的是低阶模态，本文模态分析仅关注前十阶固有频率及振型[19]。

3 结果讨论

3.1 双向流固耦合网格无关性

采用CFD软件进行流固耦合仿真时，计算结果对网格划分情况是十分敏感的[20]。本研究采用不同单元数目的流体单元(单元类型Fluid30)进行流体计算；以及采用不同单元数目的Solid186结构单元和Shell181壳单元计算管道结构。各单元参数如表1所示。

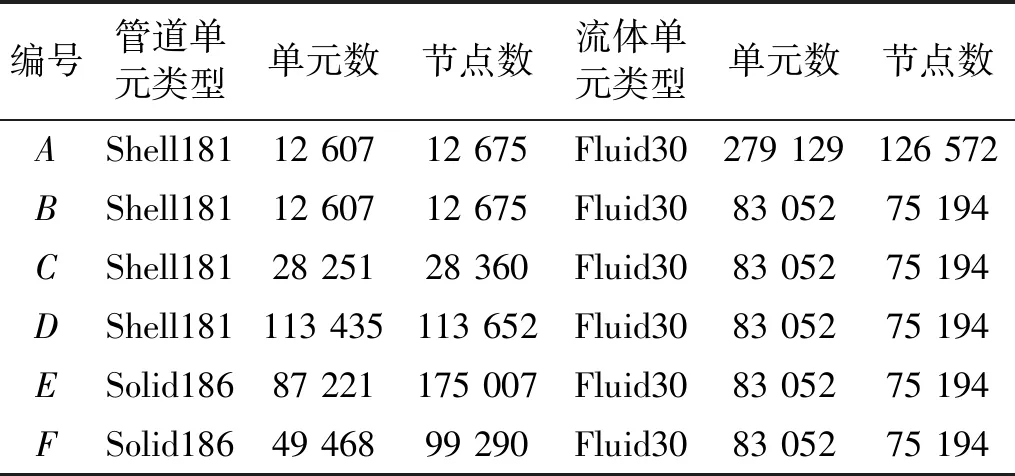
表1 管道及流体单元参数Tab.1 The pipes and the fluid elements parameters

以不同单元类型计算，分析A，B两进口流速均为5 m/s，流体压强值为2 MPa时的管道振动特性，得到的前十阶固有频率如图2所示。

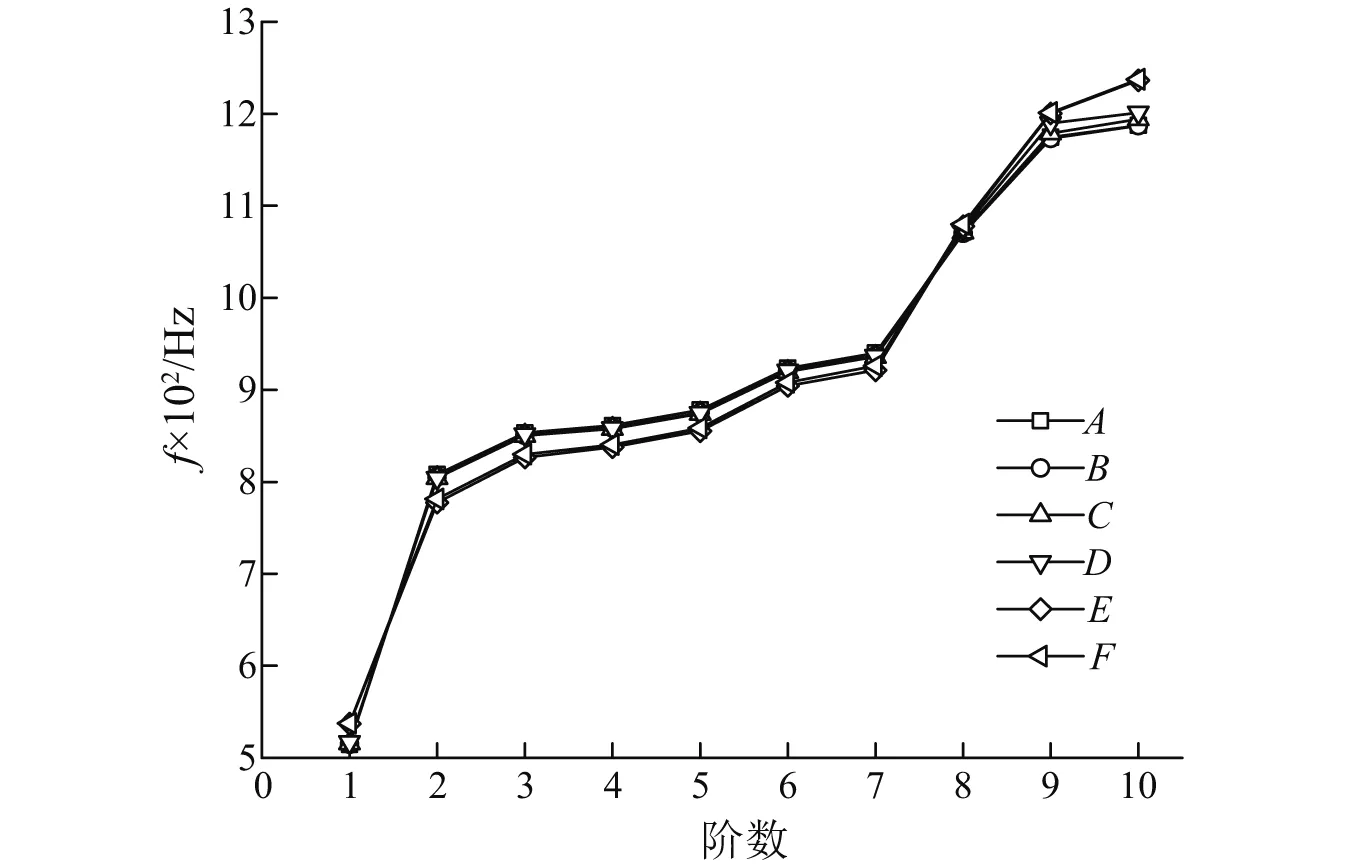
图2 不同单元参数的T型管固有频率Fig.2 Natural frequencies of T-shaped pipe of different elements parameters

Fluid30单元有8个节点，每个节点4个自由度：x，y，z方向平动和压力。但只有在流固耦合面上的平动才有效[21]。对比A，B两种情况下的固有频率，可以看到，流体单元数对结果影响不大。Shell181壳单元适合于薄至中等厚度的壳结构，由4个节点定义，每个节点6个自由度。对比B，C，D三种不同单元数的壳单元，可以看出各阶固有频率无明显变化。但是与E，F对比发现，使用Solid186单元得到的固有频率与Shell单元差别很大，第2～第7阶频率小于使用壳单元计算得到的频率，考虑管道壁厚只有2 mm，以及节约计算资源，流体使用Fluid30单元(单元数83 052，网格节点数75 194)，管道选用Shell181壳单元[22](单元数12 607，节点数12 675)进行后面的分析。

3.2 不同耦合方法下的固有频率分析

当流体压强为2 MPa，A,B两进口端流速均为5 m/s，流体为水时。T型管空管模态分析，单向流固耦合法模态分析和双向流固耦合法模态分析得到的各阶固有频率见表2。

表2 三种计算方式下管道的固有频率Tab.2 Natural frequencies of pipes in three different calculation modes

流体作用对于T型管固有频率存在较大影响，从表2中可以看到对于前十阶固有频率，考虑流固耦合与不考虑流固耦合之间的固有频率相差达9%～12%。单向流固耦合法得到的管道各阶固有频率均高于双向流固耦合法的固有频率，这是因为单向流固耦合只考虑流体对管路的作用，没有考虑到管路对流体的影响，得到的管道预应力较大。

图3为不同计算方法下的T型管前三阶振型图。可以发现：三种计算方法中，相同阶次下的振型形态基本一致，振幅分布位置相似，振幅幅值略有差异，单向耦合和双向耦合作用时的最大振幅比空管结构振幅略大。因此流体运动对T型管的振动存在显著影响，在振动分析中需要考虑流固耦合的作用。

3.3 流体压强对管道的影响

在A，B两个进水口水流速度均为5 m/s情况下，利用双向流固耦合方法进行T型管模态分析，计算流体压强为2 MPa，4 MPa，6 MPa，8 MPa时的T型管固有频率，得到的不同的流体压强的前十阶固有频率如图4所示。从图4中不难发现，在一定的流体压强范围内( 2～8 MPa)，管道各阶固有频率随流体压强增加而增加，管道内流体压强对T型管固有频率有较大影响，因此在设计管道系统时，流体压强要作为主要的固有频率分析影响因素考虑。

在T型管的结合处有一个高应力区域，垂直方向的流体在这个位置冲击管道，流体流动状态被改变，流体对管壁的作用力变大。流体压力与管道壁面之间发生强烈的泊松耦合与结合部耦合。泊松耦合对充流T型管影响最为明显，管壁受到的作用力导致显著的形变。当流体压强为2 MPa时，最大总变形量为0.196 mm，随着压强增大，总变形量增大，当压强为8 MPa时，最大总变形量达到0.676 mm。等效应力显示相同变化规律。

图3 不同计算方法的前三阶振型Fig.3 The natural vibration modes of different calculation methods

图4 不同流体压强下的T型管固有频率Fig.4 Natural frequencies of T-shaped pipe of different fluid pressures

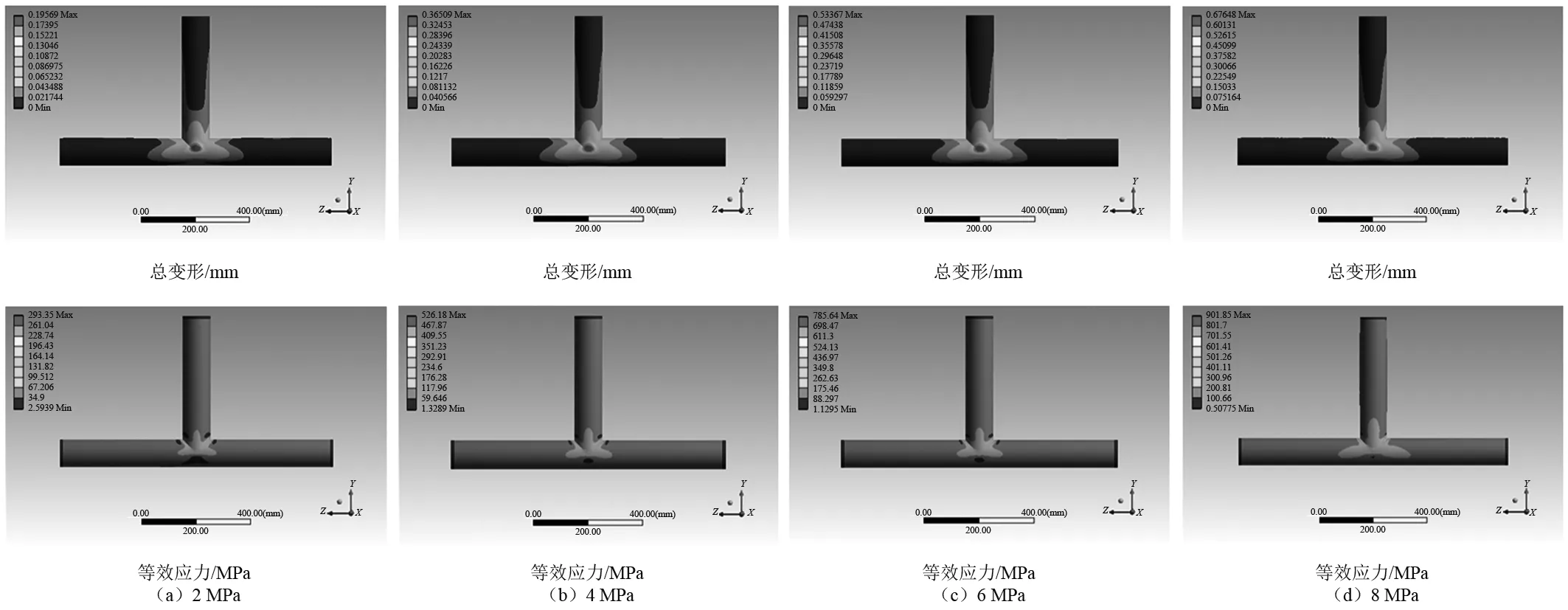
图5 不同流体压强时的T型管总变形和等效应力图Fig.5 Total deformation and von-mises stress diagram of T-shaped pipe at different fluid pressures

3.4 不同流体速度对固有频率的影响

固定T型管主管进口(B进口)进口速度为5 m/s，分支管(A进口)进口速度分别为5 m/s，10 m/s，15 m/s和20 m/s，T型管出口(D出口)设置为0 MPa情况下，得到的管道固有频率如图6所示。从图6中可以看到，各阶固有频率变化不明显，相比于流体压强，支管进口速度对T型管固有频率的影响较小[23]。

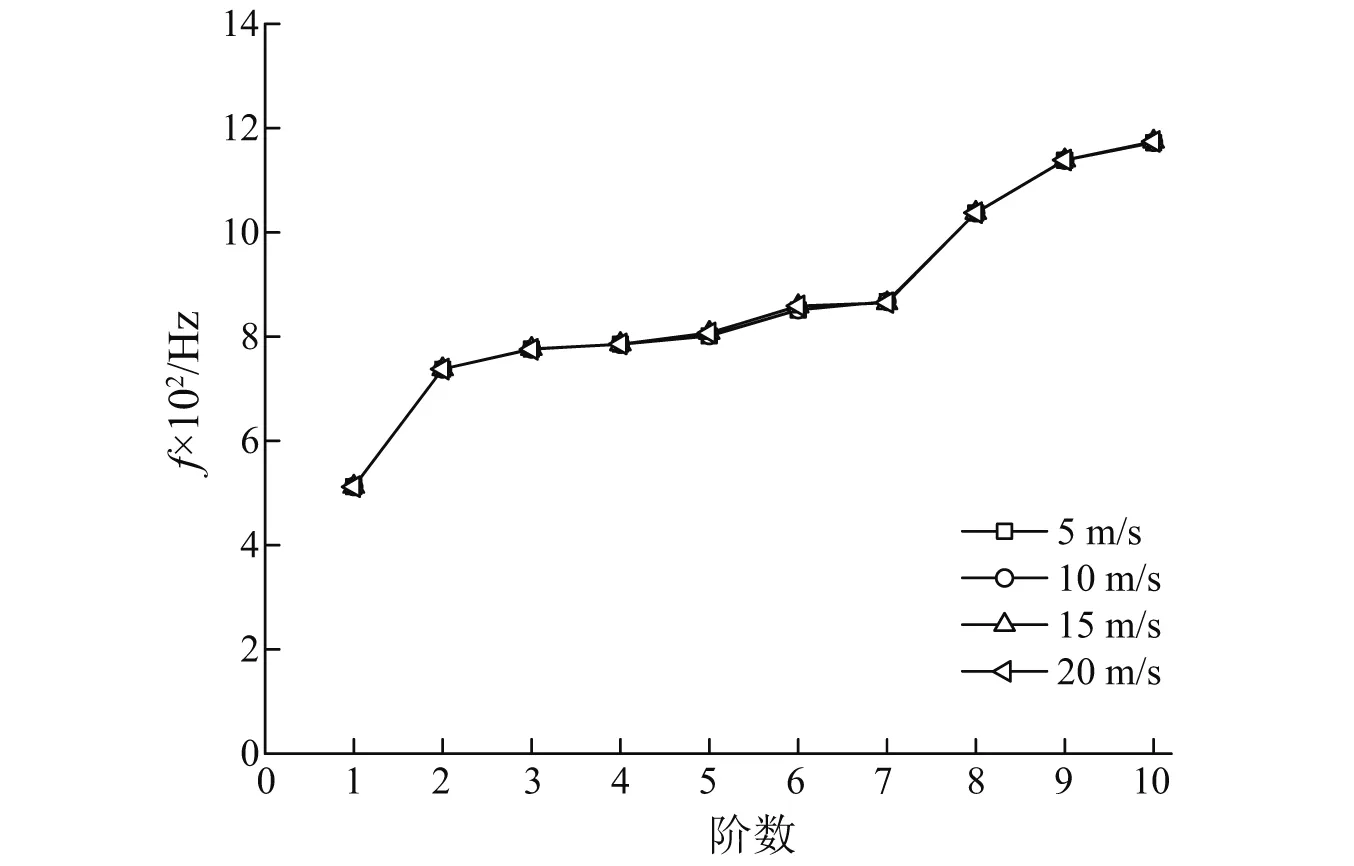
图6 不同分支管流速下的T型管固有频率Fig.6 Natural frequencies of T-shaped pipe of different branch pipe fluid speeds

在不同分支管进口速度情况下，管道的变形和等效应力存在差异，除了在T型管结合部位出现变形和应力最大值，在T型管结合处流体汇合的下游部位出现变形和应力集中区域。从图7中可以发现，当分支管进口速度为20 m/s时，最大总变形量为0.046 8 mm，分支管进口速度为5 m/s时，最大总变形量为仅相当于20 m/s时的10%，等效应力与总变形量趋势相同。支管速度越大对T型管结合处以及下游壁面的剪切应力越大，流动侵蚀加剧。由于长时间处于高应力条件下，容易导致管道壁面侵蚀，焊缝开裂，寿命减少[24]。

图7 不同分支管流速下的T型管总变形和等效应力图Fig.7 Total deformation and von-mises stress diagram of T-shaped pipe at different branch pipe fluid speeds

3.5 不同流体密度对固有频率的影响

压力管道应用于多种场合，不同流体对管道固有频率影响不同。为研究不同流体密度对T型管固有频率影响，这里选取水，液压油，90#汽油和液化石油气作为不同密度的流体，进行T型管双向流固耦合模拟分析，材料特性见表3所示。

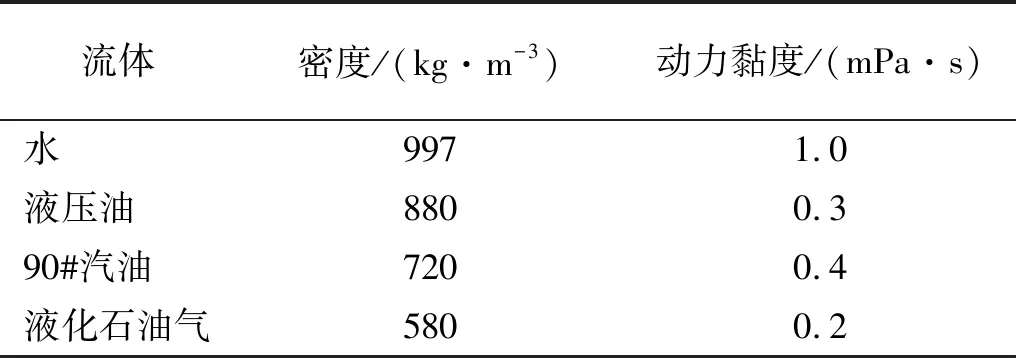
表3 流体特性Tab.3 Fluid properties

在管道压强为2 MPa情况下，T型管两个进口速度分别为5 m/s时。利用双向流固耦合方法进行T型管模态分析，得到的前十阶固有频率如图8所示。

图8 不同流体密度的T型管固有频率Fig.8 Natural frequencies of T-shaped pipe of different fluid density

从图8中可以发现，不同的流体具有不同的密度和动力黏度，但是在相同的边界条件下，T型管的固有频率差异很小。从图9中可以看到，管道等效应力随流体密度的减小而减小，但差别不大。设计计算中可以作为次要因素考虑。

图9 不同流体密度的T型管总变形和等效应力图Fig.9 Total deformation and von-mises stress diagram of tee pipes at different fluid density

3.6 谐响应分析结果

基于对流固耦合管道模态分析结果，采用模态叠加法(Mode Superposition)对T型管进行谐响应分析。模态叠加法通过对模态分析得到的振型(特征向量)乘上因子并求和来计算出结构的响应，它的优点是：能够使解按照结构的固有频率聚集，响应曲线可以更平滑，更精确。

对T型管进行谐响应分析时，激振幅值为0.5 MPa。对比之前的模态分析结果，设置管道激励频率范围设置为0～1 500 Hz，其中包括了T型管前十阶固有频率。选取管道结合处两条焊缝交汇点作为重点监测位置，分析T型管的位移，加速度，应力和应变与激励频率之间的响应关系.。

通过对焊缝交汇点C的振动谐响应分析，得出的x,y,z方向上位移、应力及应变与激励频率之间的响应曲线，如图10所示。

图10 振动特性响应曲线Fig.10 Vibration characteristic response curve

从图10中可以发现：随着激励频率的增大，焊缝结合处点C的位移，加速度，应力及应变都会在第2阶固有频率(约800 Hz)和第8阶(约1 060 Hz)固有频率附近出现峰值。对比模态分析结果和谐响应曲线，最大峰值与固有频率之间的差异主要是在输出数据提取时设置间隔为20 Hz，但是响应峰值频率与第2阶和第8阶固有频率之间误差分别为0.56%和0.85%，对研究结果影响不大。

在图10(a)和图10(b)中，由于管道进出口端被固定，所以z方向上C点位移几乎为0。激励频率为800 Hz时，x方向和y方向的位移峰值分别达到0.246 21 mm和7.43×10-2mm。激励频率为1 060 Hz时，x方向和y方向的位移峰值分别达到0.118 26 mm和3.89×10-2mm。并且可以发现，由于进出口端固定，y方向和z方向上加速度响应几乎为零，激励频率为800 Hz时，x方向上的加速度峰值为6.22×106mm·s-2，激励频率为1 060 Hz时，x方向上的加速度峰值为5.25×106mm·s-2。在管道系统设计和结构优化中可以对垂直x方向上进行约束，减小振动。

在图10(c)和图10(d)中，由于存在垂直的y方向上的流体冲击，C点位置y方向上的应力应变响应是最大的，激励频率为800 Hz时，y方向上的应力响应达到32.942 MPa。应变响应达到1.55×10-4mm/mm。激励频率为1 060 Hz时，y方向上的应力响应达到18.467 MPa。应变响应达到1.23×10-4mm/mm。T型管结合处附近可以作为振动传感器安装位置，对管道进行压力与速度的振动数据监测。这些分析可以为管道结构的设计与优化提供技术支持与理论依据。