基于高阶阻抗传递函数的车辆ISD悬架优化设计与性能分析

2019-12-02沈钰杰刘雁玲杨晓峰仇成群

振动与冲击 2019年22期

沈钰杰，刘雁玲，陈龙，杨晓峰，仇成群

(江苏大学汽车工程研究院，江苏镇江 212013)

新型被动车辆ISD(Inerter-Spring-Damper)[1-3]悬架系统由于其优越的隔振性能，目前已受到工程领域的广泛关注。车辆ISD悬架系统中的核心元件惯容器[4]的提出，完善了机电相似性理论中的不完全对应现象[5]，因此，可以将电学网络中成熟的理论应用于机械网络系统的设计。电学系统中无源网络综合理论[6]的核心思想是利用电感、电阻和电容元件将已知阻抗传递函数进行被动实现。对应到机械网络中，即可应用弹簧、阻尼器和惯容器对其进行综合实现。近年来，国内外学者围绕机械网络的无源网络综合开展了新一轮研究，证实了其在机械隔振领域的有益效果[7-11]。

文献[12]最早研究了应用线性矩阵不等式的方法对车辆ISD悬架系统进行网络综合优化设计，结果表明悬架的综合性能可以得到有效提升。文献[13]在原有的双二次型阻抗传递函数基础上，进一步研究了双三次型阻抗传递函数对火车悬架性能提升的效果，结果显示，双三次型阻抗传递函数相较于双二次型阻抗传递函数，其性能可得到显著改善。然而，在车辆悬架系统的结构设计中，高阶阻抗传递函数对应的网络元件数量众多，单纯的机械网络难以工程实现与应用。机电惯容器[14]是近年来提出的一种新型惯容器实现装置，其利用机械式惯容器与电机进行耦合设计的结构方案，通过电机外端网络的电阻抗模拟实现目标机械阻抗的方式，为实现复杂的网络结构提供了新的解决途径。

因此，本文以应用机电惯容器的车辆ISD悬架作为研究对象，探索应用高阶阻抗传递函数进行车辆ISD悬架系统结构设计的提升效果，通过筛选机电惯容器的结构特征，对高阶阻抗传递函数进行降阶转换，并利用改进的粒子群算法对其进行优化求解，最终给出悬架系统的具体实现方案，力图给车辆ISD悬架的研究提供新的思路。

1 基于高阶阻抗传递函数的悬架模型构建

本文选取双三次型阻抗传递函数作为研究对象，构建了车辆1/4悬架动力学模型，如图1所示。

图1 车辆1/4悬架模型Fig.1 Quarter car model

图1中：ms为簧载质量；mu为非簧载质量；K为悬架弹性元件的刚度；Kt为轮胎的等效弹簧刚度；zr为路面垂向的位移输入；zu为非簧载质量的垂向位移；zs为簧载质量的垂向位移；T(s)为待优化设计的悬架系统阻抗表达式。根据牛顿第二运动定律，可以得到车辆1/4悬架模型的动力学拉氏方程为

mss2Zs+[K+sT(s)](Zs-Zu)=0

(1)

mus2Zu-[K+sT(s)](Zs-Zu)+Kt(Zu-Zr)=0

(2)

式中：Zr，Zu与Zs为相应变量的拉普拉斯变换形式；s为拉氏变量。悬架系统的模型参数如表1所示。

表1 悬架模型参数Tab.1 Parameters of suspension model

T(s)为双三次速度型阻抗传递函数，其标准形式的表达式为

(3)

式中：A，B，C，D，E，F，G，H≥0；E，F，G与H不全为0。由于所设计的车辆ISD悬架是被动型悬架系统，其需满足的正实性约束条件为[15]

(C+G)(B+F)≥(D+H)(A+E)

(4)

(5)

当a3>0，a0≥0时,

(6)

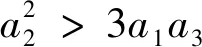
(7)

(8)

其中，

a0=DH

(9)

a1=CG-DF-BH

(10)

a2=BF-CE-AG

(11)

a3=AE

(12)

从式(4)～式(12)可知，若以双三次型阻抗传递函数作为研究对象，其可以被动实现的条件，即正实条件较为复杂，且网络综合过程繁琐，不易于工程化实现。根据Bott-Duffin无变压器综合法[16]可知，双三次型阻抗传递函数的网络综合需要用最多13个元件串并联进行被动实现。因此，可以考虑根据现有的结构特征对其进行降阶转换。

2 高阶阻抗传递函数的降阶转换

由Brune综合法及Bott-Duffin综合法的基本变换Foster循环[17]可知，串联或并联地提取出一个电抗元件(电感或电容)可使得原传递函数的阶数降低；串联或并联地提取出一个电阻元件(电阻)则不改变原传递函数的阶数。

当选择机电惯容器作为机械网络与电网络之间的电信号与机械力信号的传递装置时，机电惯容器始终存在于悬架系统中，且始终与外端负载电路的电网络阻抗相并联。因此，本文对原双三次型阻抗传递函数作如下变换：

步骤1分别串联或并联地提取出一个阻尼器元件；

步骤2并联地提取出一个惯容器元件。

其中，步骤1不仅不改变原双三次型阻抗传递函数的阶数，而且避免了结构的遗漏。步骤2中由于所述机电惯质的电网络与机械式惯容器始终并联，因此并联的提取出惯容器元件，由此实现了原双三次型阻抗传递函数的降阶转换。经由步骤1与步骤2变换后得到的悬架结构示意图如图2所示。

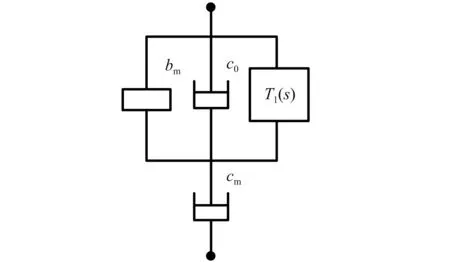
图2 降阶转换示意图Fig.2 Schematic of reducing order

图2中：bm为机械式惯容器；c0与cm为机械阻尼器；其中c0为0或cm为无穷大。此时，转换后的悬架结构速度型阻抗表达式为

(13)

经过变换后的阻抗传递函数T1(s)为双二次型，其标准型表达式为

(14)

而式(14)为正实函数[18]的充要条件是

(15)

应用以上的变换方法，具有以下优势：

(1) 通过Foster循环步骤提取得到的元件可以作为悬架的机械网络基础结构，即当电网络失效时，同样可以具有相应隔振性能的悬架系统；

(2) 将原有的双三次型阻抗传递函数通过Foster循环步骤实现了降阶，有效解决了高复杂度阻抗传递函数的网络综合过程，使得具体的悬架结构更容易通过网络综合实现。

可以得到降阶转换前后传递函数系数之间的关系式为

A=bmcmD0

(16)

B=cm(bmE0+c0D0+A0)

(17)

C=cm(bmF0+c0E0+B0)

(18)

D=cm(c0F0+C0)

(19)

E=bmD0

(20)

F=cmD0+bmE0+c0D0+A0

(21)

G=cmE0+bmF0+c0E0+B0

(22)

H=c0F0+cmF0+C0

(23)

3 参数优化

3.1 优化目标的选取

车辆在行驶过程中，既要满足良好的舒适性要求与轮胎的接地性要求，同时悬架的动行程应满足一定的约束范围，以防止悬架撞击车身影响舒适性。因此，本文综合考虑在随机路面输入条件下的车身加速度均方根J1、悬架动行程均方根J2以及轮胎动载荷均方根J3为优化目标，将多目标函数进行线性组合转换为单目标函数[19]。其具体表达式为

(24)

式中：J1，J2与J3为待优化的车辆ISD悬架车身加速度均方根、悬架动行程均方根与轮胎动载荷均方根；J1pas，J2pas与J3pas分别为传统被动悬架的车身加速度均方根、悬架动行程均方根与轮胎动载荷均方根。假设汽车以40 km/h的车速行驶在C级路面上，仿真时长为10 s，采样时间为0.001 s。

3.2 优化约束条件

3.2.1 传递函数的正实性约束

本文所要优化的变量为bm，c0，cm，A0，B0，C0，D0，E0，F0共9个参数，根据机械网络元件的存在性意义可知，优化变量的约束范围为

(25)

式中：D0，E0，F0不全为0。此外，要满足T1(s)为正实函数，还需满足式(15)所给出的约束条件。

3.2.2 悬架系统性能的约束

在优化过程中，将传统被动悬架的三个性能指标作为对比约束指标，当适应度函数值超出其约束条件时，将适应度函数进行惩罚，惩罚规则为将其与一个较大的数值相加，本文取100 000。悬架的性能约束条件为

J1≤J1pas,J2≤J2pas,J3≤J3pas

(26)

3.3 优化算法的设置

本文采用改进的多种群粒子群算法中同时包含多个种群，并行的种群数量设为20。种群中粒子的位置与速度更新规则为

(27)

所述改进的粒子群算法各种群间的进化过程相对独立，同时包含交叉与变异操作。其中，交叉操作的位置产生规则如式(28)所示

a1=rand(n),a2=rand(n)

(28)

式中：a1与a2为选择的交叉个体位置。交叉操作的具体表述为

(a1≠a2)&(fa1≠fbest)&(fa2≠fbest)

(29)

式中：fa1，fa2为对应位置个体的适应度值；fbest为最优个体的适应度值。所述变异操作的实现条件为

fn>fn+1

(30)

式中：fn为变异之前的适应度函数值；fn+1为变异之后的适应度函数值。

表2 优化参数Tab.2 Optimized parameters

可以得到的所设计的双三次型阻抗传递函数的表达式为

经过降阶转换得到的双二次型阻抗传递函数的表达式为

优化得到的双三次型阻抗传递函数与双二次型阻抗传递函数Bode图，如图3所示。

从图3可知，优化得到的双二次型阻抗传递函数T1(s)与双三次型阻抗传递函数T(s)在低频段均呈现出惯性特性。对于T1(s)来说，随着频率的增加，其惯性特性逐渐转变为刚度特性，且过渡段平稳无波动。而对于T(s)来说，随着频率的增加，其惯性特性也逐渐减小并转变为阻尼特性。需要指出的是，由“弹簧-阻尼器”二类机械元件组成的传统悬架系统中则无法呈现出惯性特性，这便是传统悬架结构性能提升受到限制的主要因素，也是含有惯容器的车辆ISD悬架具备更优越隔振性能的原因所在。

图3 优化结构Bode图Fig.3 Bode scheme of the optimized structure

4 仿真分析

4.1 频域分析

若将悬架系统看做一个整体阻抗传递函数：TT(s)，通过对悬架动力学模型的分析计算，分别得到车身加速度对路面输入垂向位移的频响函数为

(31)

悬架动行程对路面输入垂向位移的频响函数为

(32)

轮胎动载荷对路面输入垂向位移的频响函数为

(33)

图4～图6分别为悬架系统的车身加速度增益对照图，悬架动行程增益对照图和轮胎动载荷增益对照图。

从图4～图6可知，相较于传统被动悬架，车辆ISD悬架系统的隔振性能有了较为显著的提升。从车身加速度增益图可以看出，在低频与高频的两个共振峰值处，车辆ISD悬架的共振峰值明显小于传统被动悬架，其中车身加速度增益在低频段的共振峰值降低了42.7%，高频共振峰值降低了2.8%，低频段的改善效果比高频段更为显著。而在中频段2～10 Hz，车辆ISD悬架的车身加速度增益相较于传统被动悬架略有恶化。

对于悬架动行程增益来说，从其增益图可以看出，本文研究的车辆ISD悬架在全频域范围内均优于传统被动悬架，其中，悬架动行程增益在低频段的共振峰值降低了36.4%，高频共振峰值降低了28.7%，改善效果较为明显。

图4 车身加速度增益图Fig.4 Gain of vehicle body acceleration

图5 悬架动行程增益图Fig.5 Gain of suspension working space

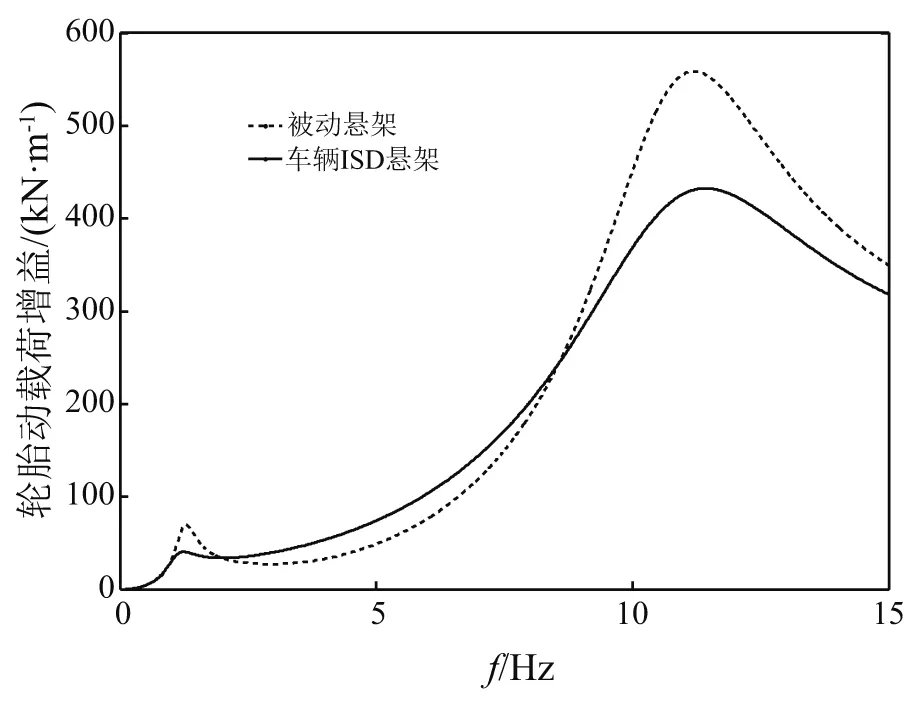
图6 轮胎动载荷增益图Fig.6 Gain of dynamic tire load

对于轮胎动载荷增益而言，其相对趋势与车身加速度相同，在低频与高频共振处的峰值均得到有效抑制，其中，低频段的共振峰值降低了42.0%，高频共振峰值降低了22.6%。高频共振处峰值的改善较之车身加速度增益的改善更为明显，然而在中频段2～8 Hz内，其增益值相较于传统被动悬架均略有恶化。

4.2 时域分析

假设车辆行驶在C级路面，仿真中采用的路面输入模型[20]如式(34)所示

(34)

式中：u为行驶车速；zr(t)为路面的不平度的垂向输入位移；Gq(n0)为路面不平度系数；w(t)为白噪声信号。图7～图10分别给出了车速为40 km/h条件下路面输入曲线时域图、车身加速度响应曲线、悬架动行程响应曲线和轮胎动载荷响应曲线。表3给出了不同车速的随机路面输入条件下，车辆ISD悬架与传统被动悬架的动态响应指标对照表。

图7 路面输入曲线Fig.7 Random road input

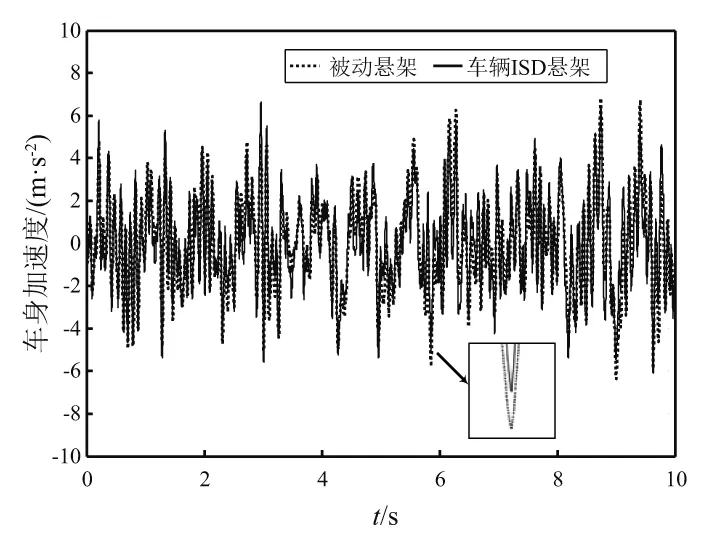
图8 车身加速度响应曲线Fig.8 Vehicle body acceleration in time domain

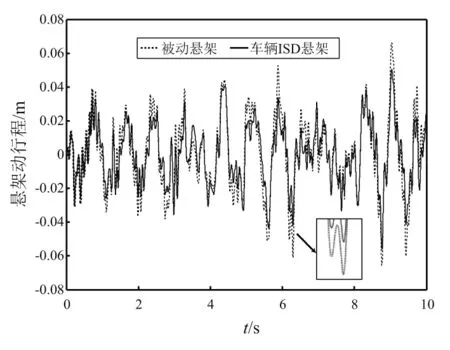
图9 悬架动行程响应曲线Fig.9 Suspension working space in time domain

图10 轮胎动载荷响应曲线Fig.10 Dynamic tire load in time domain

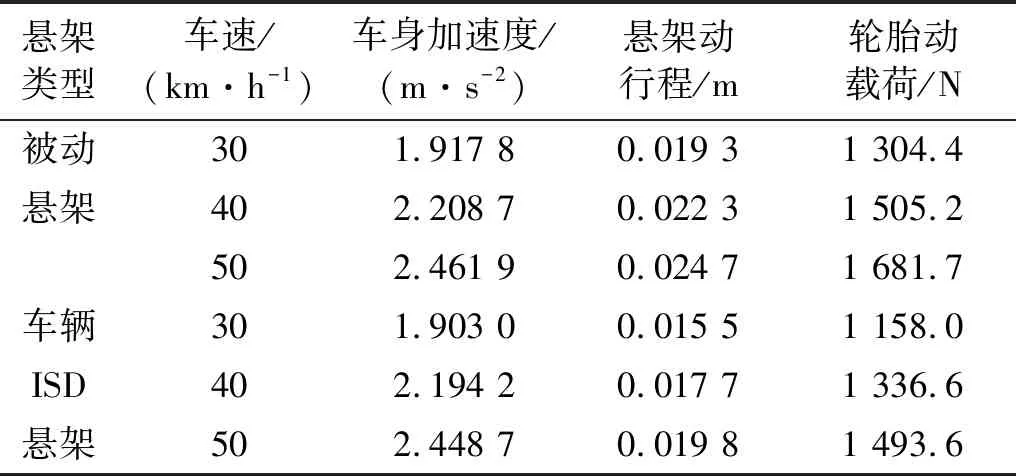
表3 随机路面输入条件下性能指标对照表Tab.3 Performance indexes in random road input

相较于传统被动悬架，本文研究的车辆ISD悬架的隔振性能具有显著的优势。其中，在车速为30 km/h，40 km/h和50 km/h条件下，悬架动行程均方根值分别减小了19.69%，20.63%和19.84%，轮胎动载荷均方根值分别减小了11.22%，11.20%和11.19%，而车身加速度均方根的提升效果较小，分别仅降低了0.77%，0.66%和0.54%。总体而言，相较于传统被动悬架，车辆ISD悬架系统的隔振性能得到了有效的提升。

5 高阶阻抗传递函数的网络综合实现

根据双二次型阻抗传递函数网络综合实现的最简实现判据可知，本文优化得到的T1(s)满足Jiang等提出的正则(Regular)条件，可用5个元件串并联进行被动实现。其对应的电网络图和机械网络图分别如图11和图12所示。

从图11和图12可知，双二次型阻抗传递函数可用三个阻尼器、一个弹簧和一个惯容器元件组成，对应到电网络中即为三个电阻元件、一个电感元件和一个电容元件。以图12为例，表4给出了机械网络元件参数的具体数值。

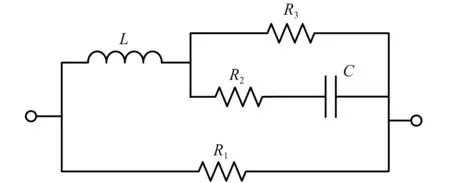
图11 电网络元件图Fig.11 Electric network elements

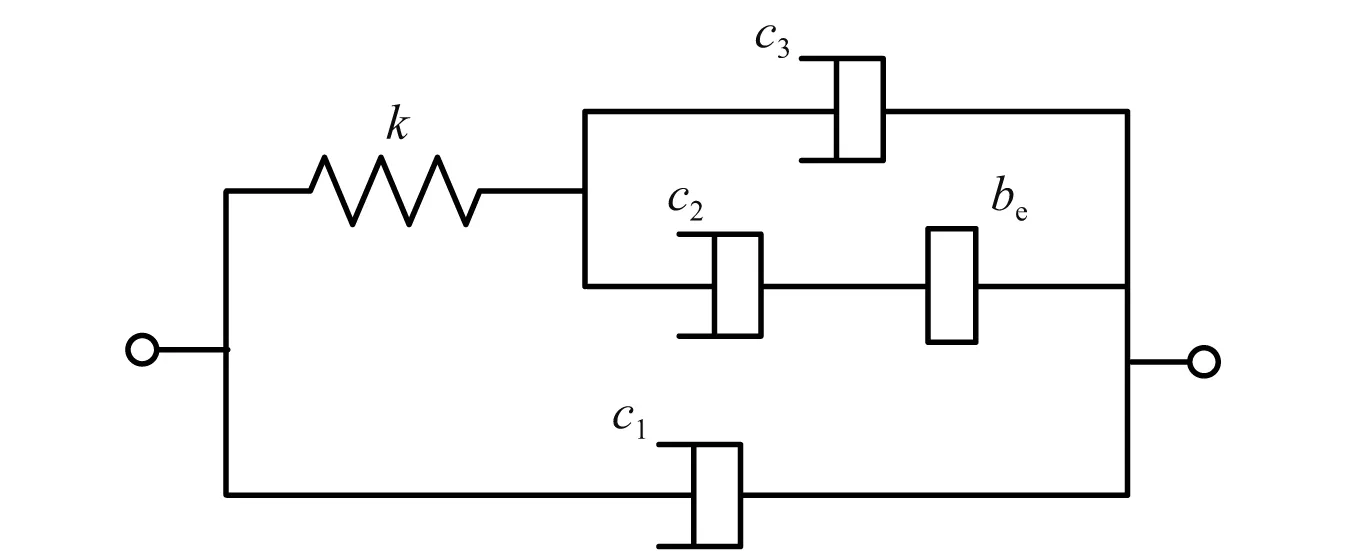
图12 机械网络元件图Fig.12 Mechanical network elements

名称数值悬架弹簧刚度K/(N·m-1)22 000惯质系数bm/kg93.57惯质系数be/kg474.36阻尼系数cm/(N·s·m-1)1 840.98阻尼系数c1/(N·s·m-1)1.04阻尼系数c2/(N·s·m-1)10 800.15阻尼系数c3/(N·s·m-1)1.32弹簧刚度k/(N·m-1)613 961

当所选用的结构方案为机械网络元件时，如表4所示。所设计的车辆ISD悬架共有8个元件(包含支撑弹簧元件)组成，在工程上难以实现，因此可以考虑利用如图11所示的等效电网络元件对其进行模拟实现，便于工程应用。