素养指向下深度教学的实践与探索

王山林　张瀚斤

中图分类号：G633.6    文献标识码：B    文章编号：1009-010X（2019）29-0047-05

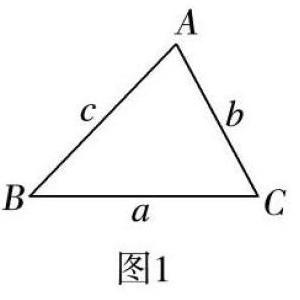
2019年3月22日，在石家庄市教育科学研究所组织的“素养指向的深度教学‘京冀名师工作室教学研讨活动”中，北京11学校的张瀚斤老师作了一节示范课（人教版教材七年级下册“三角形内角和定理”第1课时）。笔者有幸到会观摩学习，结合该课例作以下分析，愿与数学同仁分享。

一、回顾旧知，引发思考

1.师：请同学们说一说：你在对一个命题进行说理时，通常是怎么理清思路的？

生1：我先找到题中的已知条件，然后确定要找到的目标，通过已知条件得知我所知道的角和线段它们之间的关系，然后一步一步推导出来。

师：老师能感觉到同学们对这个问题是有一定了解的，通过本节课对三角形知识的学习，我们会对这个问题有更深入的理解。

【分析】课始，并没有采取“创设情境”的“时尚”做法，而是单刀直入回忆如何“说理”。根据具体教学内容，采取适当的教学引入，而不是为情境而情境。一方面抓住了本单元的重点“训练学生规范的表达”;另一方面抓住了新知所需的基础“如何思考问题”。学生要回答这个问题，就需在调用原有经验的基础上，组织语言，进行归纳、表达。

2.师：我们学习了关于三角形三条边关系的一个重要结论是什么？

生2：两边之和大于第三边。

师：研究三角形可以从角和边入手研究边与边的关系、角与角的关系、边与角的关系。请你推测一下，这节课会从哪个角度研究三角形呢？

生3：从“角”的角度。

师：咱们学过从“角”的角度刻画三角形的相关结论吗？

生4：从角的角度划分，有锐角三角形、直角三角形、钝角三角形。

生5：三角形内角和是180°。

生6：三角形的外角等于不相邻的两个内角之和。

师：真厉害，都知道后边要学的内容了。刚才同学们提到的确实是咱们这节课要学习的，就是“三角形内角和定理”。

【分析】让学生去推测研究内容，是培养问题意识，培养提出问题能力的策略。让学生推测不仅仅是简单的提出推测要求，而是给出了推测的基础，让学生能猜测;给出了推测的方向，使学生不乱猜测，有推测的价值，结果是本课需深入研究的问题。由推测进而思考已有相关知识储备，已经隐含了解决问题的一般思路，对学生起到潜移默化的作用。

3.师：在小学阶段我们学过“三角形的内角和都是180°”，回忆一下，小学是怎么说明这个结论是正确的呢？

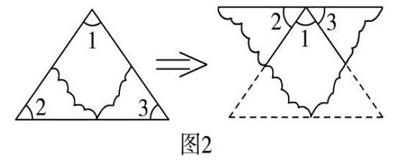
生7：小學是把三个角剪下，并将它们的顶点重合在一起，将它们的相应边重合在一起，形成一个平角，这说明了三角形的内角和是180°。（师出示图2）

生8：用量角器量的方法。

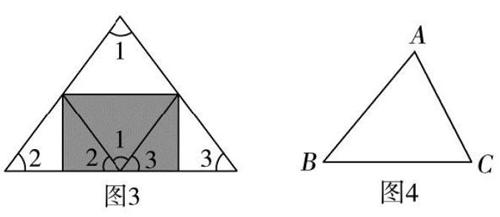
师：很好，是不是还有折拼的方法（图3）：

这样折拼看起来也是一个平角。

师：有同学对原来的研究方法有什么质疑吗？

生9：我感觉原来都是目测的，测量有可能有误差。

师：这确实是原来咱们在实验阶段存在的局限性，所以今天我们又拿出来，看能否从逻辑说理的角度去把这件事情证明清楚。

【分析】在回忆旧知的过程中比较、分析、反思，引导学生认识已有知识的局限性，培养了抽象思维能力、反思能力、质疑精神，并达到引发对新问题探究的欲望之目的——从逻辑说理的角度去把事情证明清楚。

4.师：先看学习单第1小题：与180°相关的定理和定义有哪些？

生10：平角都是180°的角。

生11：三角形内角和是180°。

生12：互补的两个角的和是180°。

生13：如果两条直线平行，同旁内角互补。

师：总结一下有这么两条：

1.一个平角的度数是180°。

2.两条直线平行，同旁内角互补。

师：平角是180°;两直线平行，同旁内角互补。我们的证明有没有一个明确的方向了？

生15：找平行、同旁内角。

师：对，平行、同旁内角互补或平角。但是从这个图上看既没有平角，也没有两直线平行同旁内角互补，怎么办？

生16：作辅助线。

师：对，我们要创造性地去搭建一个桥梁，使得没有平角也没有同旁内角互补的三角形走到我们思路的中间。

【分析】通过让学生回忆小学阶段学习过的“三角形”相关知识，并且在回忆过程中对学生进行积极地肯定，为学生学习新知做好了三个方面的铺垫：一是抓住新知的生长点回顾旧知，为新知识的学习做了知识上的铺垫;二是通过问题思考、回答、辨析，为解决新问题做了迁移能力上的准备，也是思维活动的预热过程;三是通过回顾旧知中相关问题的顺利解决，建立起学习新知的“脚手架”。以上教学内容通过对原有知识、原有探究经验的提取，到引导归纳出“作辅助线”，真正起到了激情诱趣、引发思考的作用，引导学生走向深层、深刻、深度学习，打好了深度教学的基础。

二、动手实践，初探新知

1.师：在学习单第2小题下面写一写：怎样说明三角形内角和是180°。

师：我发现同学们已经写出了至少一种说明方法，请你参考学习单上证明三角形内角和定理的“量规”，给自己一个评价，看自己写的怎么样。然后小组之间讨论一下，能否在别人的启示下找到更多种说理的方法。

证明三角形内角和定理的量规

【分析】在唤醒已有知识的基础上，让学生独立思考，动手操作，实验验证，尝试说理，这充分发挥了数学迁移的作用，使学生潜移默化中逐步掌握以旧知解决新问题的方法。随后，让学生利用“量规”自我评价，进一步将思维引向高阶思维——反思、评价，学生又经历一次深度分析、综合、评价的实践过程，从低阶思维走向高阶思维，这是数学抽象核心素养的提升与发展的需要。最后，小组讨论交流，思维碰撞，互相启发，重新生成。

2.师：哪个小组说一说自己是怎么解决的呢？

（3个小组的代表展示）

师：3个小组分别过A、B、C作平行线，用到

同位角、内错角，都是把三角形的三个角转化到一个平角的位置。还有其它不一样的吗？

生17：首先作CD∥AB，根据两直线平行，

内错角相等，可知∠1=∠4，再根据两直线平行同旁内角互补，我们可知∠2+∠3+∠4=180°，因∠1=∠4，所以∠1+∠2+∠3=180°.（见图5）

师：他是过点C构造了一组同旁内角，过A呢？行不行？其实，我巡视时发现还有同学跟刚才这些做法都不一样，他不过三个顶点，很有创造力的同学，来请这位同学展示一下！（见图6）

师：怎么用平行线的性质说明白这个事。

生19：平行线中同旁内角互补，

∠2+∠6=180°，∠4+∠6=180°，

所以∠2=∠4，同理∠5=∠3，∠1=∠7.

然后由对顶角定理，说明∠8=∠5，∠9=∠4，∠7=∠10，所以2∠2+2∠3+2∠1=360°，再把这个式子除以2（见图7）。

师：他用了两倍的180°，把问题说明白了。我们在做平行时并不仅仅局限于过点A、点B、点C，在三角形内部、在三角形的边上、在三角形的外面都是可以的。我们最终的目的是构造“平角”和“同旁内角”，并不局限于在哪个位置。

【分析】本环节把学习的时空交给学生，让学生充分展示探究结果，通过追问还有没有不一样的方法，促使学生发散思维。展示是最好的评价，给学生充分的展示机会，既突出了“训练学生规范的表达”，锻炼学生的语言表达能力，又引导学生进行严格的推理，培养了反思、质疑、合作交流能力，深度学习成效明显。老师抓住巡视中发现的具有创造性的特例，顺应了学生的思维，不是为突出解法多样化或一题多解，而主观上增加难度。将课堂生成资源作为新问题，引导学生深入思考，使学生思维处在愤悱状态，从而引发学生质疑、生成问题，并形成顿悟，进一步发散学生思维，培养问题解决能力。学生乐享创造的愉悦、成功的体验。

三、归纳总结，升华认知

1.师：刚才用“量规”评价达到三项示范级的同学，举手给老师看看。

师：能达到两项示范级的呢？下课结合“量规”看能不能把自己说理的过程再做进一步的改进！

【分析】用时不多，看似作用不大，实则是照应了前面布置的自评环节，在充分展示、交流后学生对“量规”中的评价标准更明确、对自己的评价更准确、对自己的不足更清晰，再次反思评价，找到差距，从思维发展来说，也是一次由“驰”到“张”的过程，利于学生在紧张思维后“反刍”，加深理解，捋顺思路。“思维之舟”暂时离开浪尖划向相对平缓的水面。

2.师：刚才同学们给出了这么多方案，有什么共同的地方？

生20：这些证法都是用我们上个单元学的平行线的性质求出来的。

生21：最终都是把三个角放在同一直线上，然后证明它们的和是180°。

生22：都作了辅助线。

师：都做了“平行”，“平行”的辅助线干了一件什么事？

生23：移角。

师：对，通俗易懂。就是实现了角的“转移”，在“转移”的过程中，我们实现了从原来什么也没有的三角形中，找到了我们想要的“平角”、“同旁内角”。

师：我们最初有一个三角形，我们想要证明它的三个内角的和是180°，于是，我们开始回忆跟180°相关的结论和定义、定理，我们想到平角的定义、两直线平行同旁内角互补，我们清楚了“起点”和“终点”之后，于是又想到构造平行线这种辅助线，通过角的转移实现从起点走向终点的连接。

【分析】在学生思维短暂的休整后，结合学生对问题的探究、展示过程，围绕如何构造“辅助线”这一难点内容，适时引导学生归纳总结。因有充分的展示、交流、评价基础，学生的表达内容真实、丰富、规范;有了充分的了解，深入的理解，学生产生了“通俗易懂”的顿悟——“移角”，转化的数学思想方法被学生形象地表达出来时，他，真明白了。数学思想方法是数学学习的灵魂，关注数学思想方法目标的落实对学生认知能力的提升会有帮助，借助于转化的数学思想的渗透，课堂上思维活动又掀起一个小高潮。

3.师：回到开始的问题：你在对一个命题进行说理的时候，通常是怎么理清思路的呢？请同学们再说一说。

生24：先看我要处理的命题，然后再进行思考，从已知知识中寻找可以使用的，然后综合地进行演绎，再构造，最后再写上去。

生25：可以先看已知条件，把已知条件标在图上。然后看问题，需要求什么，再运用已知知识构造辅助线，然后得出。

生26：如果條件需要的话，我可能会列出关键知识点的一个大纲，可以列出过去的知识解决这些问题。

师：老师这样总结合不合适：推理的关键是建立新命题与已有定理、定义的联系。

师：这个联系可能是平行线的性质，可能是平行线的判定，可能是三角形的定理，可能是我们学过的所有的定理或性质。

【分析】罗增儒教授指出，问题解决完成之后，信息过程并没有结束，“解答”依然向我们输入信息，表现为解题后的探究反思。所以，教师要发挥学生学习的组织者、参与者、引导者作用，科学把握教学进程，适时安排一个必要的环节——回顾与反思，此时，“照应”课始问题“对一个命题进行说理的时候，通常是怎么理清思路的呢？”在学生经历合情推理和演绎推理过程后，引导学生再次反思、归纳说理的一般规律。倡导学后反思，不仅完善了教学，而且提炼出对未来学习有指导作用的信息，突出了重点，梳理了思路，升华了思维。

四、巩固练习，学以致用

一个三角形中两个内角的角平分线相交所形成的钝角（如图9中∠P），与第三个角有什么样的关系？请猜想结论，并说理论证（见图9）。