基于聚类的巡检任务分配

李 彬，曾喜云，刘俊鑫

（湖南工学院数理科学与能源工程，湖南衡阳421002）

1 问题提出

某工厂为了安全生产的需要，将对26个点进行巡检，各点的位置如图1所示，两巡检点之间连线上的数字表示两点间行走耗时，每个点的巡检耗时与巡检周期如表1所示。每个点的巡检需要一名工人，求至少需要安排几名工人才能满足巡检要求？巡检点该如何分配，才能使所有点按要求完成巡检，并且每个工人的工作量比较均衡。

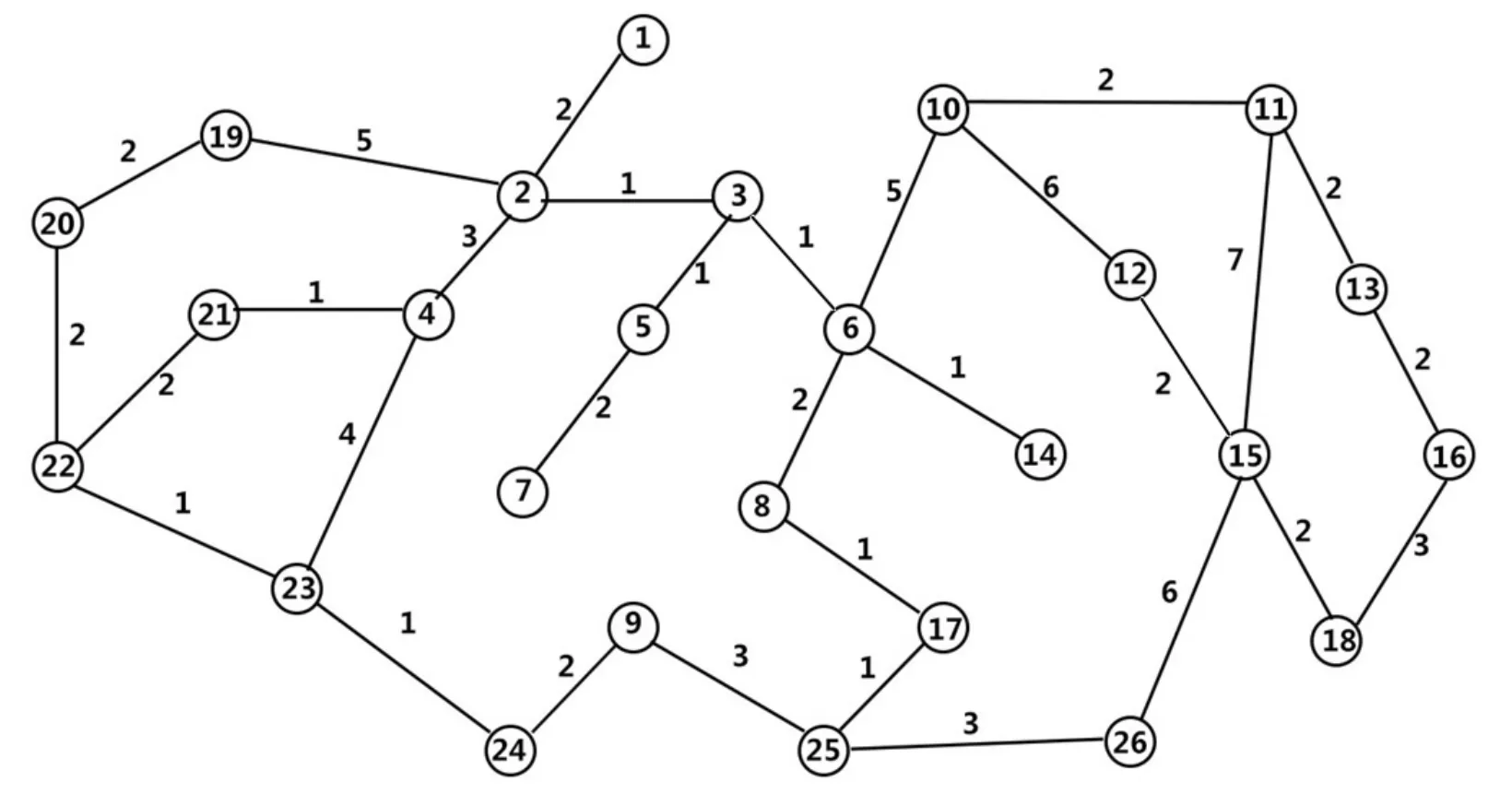
图1 巡检点连通关系

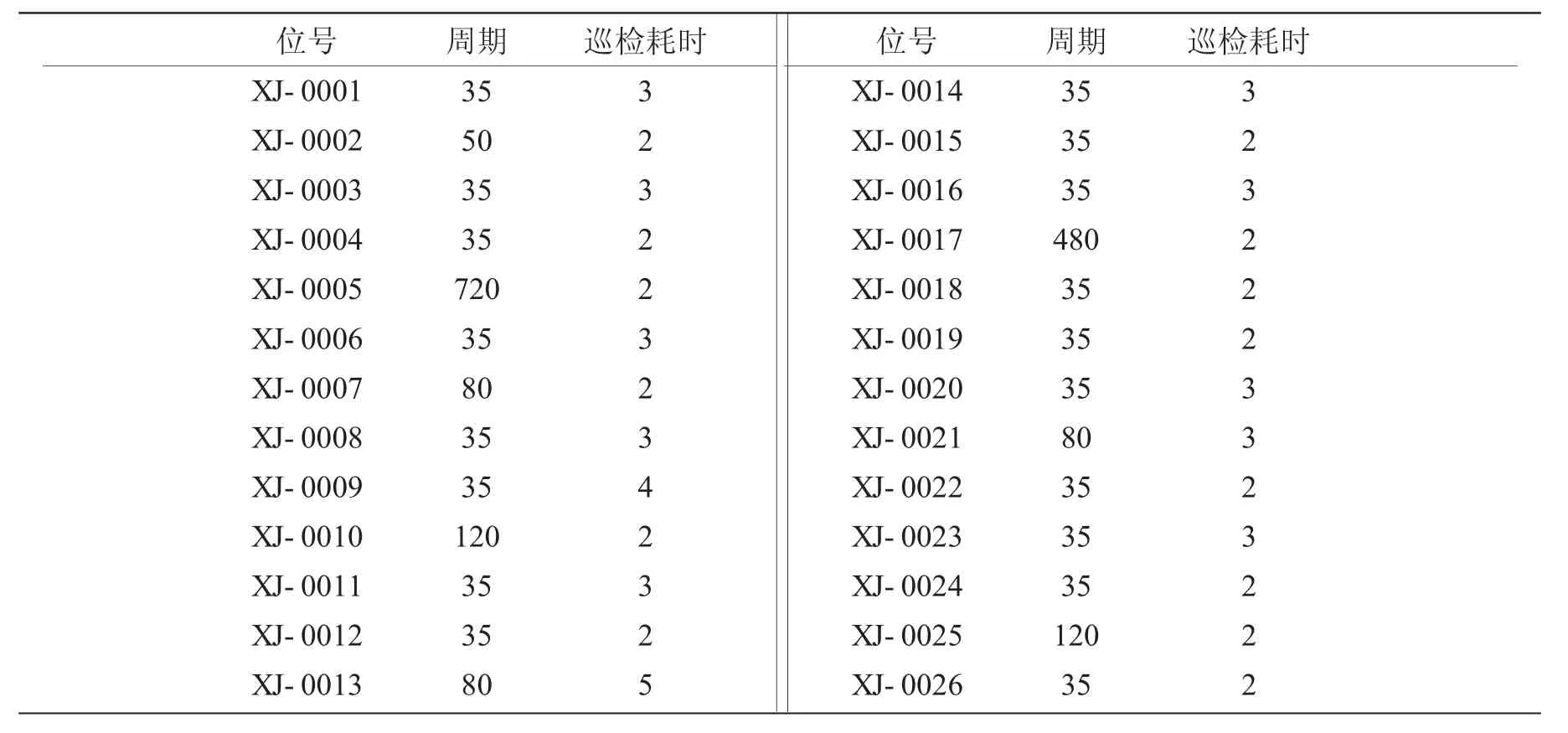
表1 巡检点耗时与周期 min

2 问题求解

2.1 巡检工人数量

设tij为第i点到第j点的最短行走耗时，根据图1各点的位置关系，利用FLOYD算法求出任意两点之间行走最短耗时矩阵t=｛tij｝26×26。现假设只有一名工人在巡检所有的点，他从某个点出发，把所有巡检点都巡检一遍再回到起点。他的总时间由两部分构成，其一是总的行走时间，这是一个26个点的TSP问题[1]，采用Lingo编程得到最短时间为68 min；其二是每个点都巡检一次的时间为67 min，总时间为135 min[2]。由于大多数巡检点的巡检周期为35 min，且，所以需要4名工人。

2.2 巡检任务的分配

把26个点分成4组，每组安排一名工人。通过聚类的方法把26个点按距离关系分成4组，建立规划模型，优化目标为分在同一组内的任意两点间的行走耗时之和趋向于较小。设tij为第i点到第j点最短行走耗时，引入如下决策变量

其中，i=1，2，3，…，26，j=1，2，3，4，建立如下规划模型

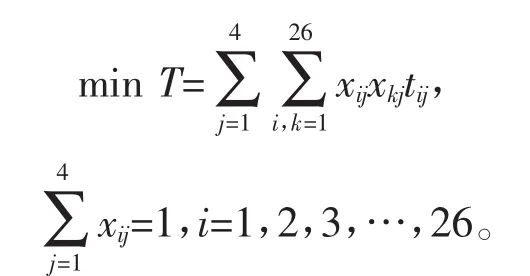
利用Lingo求得局部最优解，如表2所示。

表2 巡检点分组

2.3 各组巡检线路与工作量

每组分配一名工人，一个周期总耗时为巡检耗时与行走耗时之和。每组的行走耗时可看成TSP问题进行求解；巡检耗时为各巡检点巡检耗时之和，求得结果如表3所示。

表3 各分组巡检线路耗时 min

从结果来看，只有第2组耗时38 min，略微超过了巡检周期35 min，但第10个巡检点巡检周期为120 min，可安排每3个周期巡检一次，总体上还可减少耗时。

3 结语

本文利用聚类的方法对巡检点进行了任务分配，得出的结果较为满意，只有个别组工作量略高，但可以在聚类分组的基础上进行人工干预，对分组进行微调，较易实现工作量的均衡分配。