从用“口诀”求商到用“乘法”求商——《用2～6的乘法口诀求商》磨课与反思

孙丽芬

我们学校邀请浙江省新思维教科院参与校本研训活动已一个学期有余。在此期间，我们的教学理念和实践水平颇有变化。下面以教学《用2～6的乘法口诀求商》一课的经历为例，与大家分享个人的课堂从“教会”知识到“引导”思考的变化。

一、教学原貌

1.复习导入。

比比谁填得快——

3×（ ）=12 5×（ ）=15

3×（ ）=21 7×（ ）=14

2.创设情境，探究新知。

（1）出示例1图，讲述猴妈妈给小猴分桃的故事。

思考问题：一共有多少个桃子？猴妈妈准备分给几只小猴？

（2）尝试列式并解答。

师：12÷3=？你是怎么想的？

生：因为 3×4=12，所以 12÷3=4。口诀：三四十二。

师：这位同学是用什么方法计算的？你会吗？我们来学着他的样子算一算。

3.巩固练习，差异发展。

4.课堂小结。

【反思：这是有史以来最“高效”的课堂，笔者用了不到20分钟时间将新课上完。不到35分钟学生完成了课堂作业，还练习了口算。除了班里几个学困生还是一头雾水，其余学生计算正确率都比较高的。笔者正沾沾自喜时，班里一个乖巧的女生走过来说：“孙老师，今天学的内容我以前就会了，这节课好无趣哦！”话音刚落，其他学生也附和道：“这个太简单了，我早就会了，只要背背口诀就好了……”

学生的话促我反思：像这样的技能课怎么才能摆脱“告诉+操练”的程式，上出思考的趣味？怎么解决学生“早就会了”的问题？“早就会了”的学生有什么是“不会”的，还需要去学习的？带着这些思考，我和结对的教研员陈敏老师进行了讨论，重新设定了教学目标，把怎样求出除法算式的商作为一个开放问题，鼓励学生把除法和先前学习过的各种算法进行联系，建构合理的同时又是个性化的求商方法。】

二、教学重塑

1.情境引入。

（出示例1）

师：从图中你们知道了哪些信息？要求什么问题？

学生根据主题图回答：12个桃，每只小猴分3个。问题是：可以分给几只小猴？

师：怎样列式呢？（学生边说教师边板书“12÷3”）

师：12÷3=？真的等于4吗？我们请不会算的同学根据你对除法的理解，想办法画一画、算一算，求出12÷3的商。会算的同学，请你也画一画、算一算，检查自己的答案，等一会儿向大家说明12÷3真的等于4。

（学生尝试，教师巡回，做必要的访谈和指导）

展示学生作品。

方法1：画图法

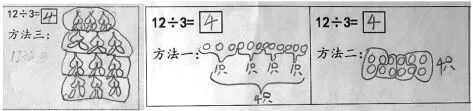
方法2：减法

方法3：加法

方法4：用口诀求商

方法5：用乘法求商

河流生态修复的技术要点为河（沟）道在平面上要宜宽则宽、宜弯则弯，蜿蜒自然，急流缓流交替出现。在纵向上保持连续，没有阻止径流的障碍物，在横断面上，无硬性阻隔，横向连通。河（沟）道生态修复技术主要包括河（沟）道防洪空间拓展技术、河流水文地貌修复技术、河流纵向连续性修复技术、河流横向连通性修复及河堤改移技术和利用生态导向方法修复的技术等。

方法6：用除法的含义求商

【反思：这次笔者设计了开放性的问题：“12÷3=？真的等于4吗？”让学生用能想到的办法尽可能清楚说明12÷3=4。鼓励学生大胆表述自己各种各样的解题过程。课堂非常热闹，学生的发言此起彼伏。正当我有些洋洋得意时，一个学生跑来对我说：“老师，最后你还是要让我们背口诀，用口诀计算这些除法算式，那为什么还要想这么多的方法呢？多麻烦！”陈敏老师也问我：“丽芬，你说这是为什么呢？为什么要教这么多方法呢？这里真的有‘这么多’方法吗？学生为什么觉得有‘这么多’方法？”

陈老师的问题使我沉静下来，在接下来的讨论中，我进一步理解到：方法多样化不是一种摆设，方法多样化的目的是释放学生多样化的理解，方法多样化的发展是使学生的理解更加深刻，即要引导学生看到方法之间的联系，看到方法的逐步演进和优化，能对方法进行沟通、改造、优化。】

陈老师指导后，笔者做了修改，最终定稿如下——

三、教学再造

1.情境引入。

（出示例1）

师：从图中你知道了哪些信息？要求什么问题？

学生根据主题图回答：12个桃，每只小猴分3个。问题是：可以分给几只小猴？

师：怎样列式呢？（学生说教师板书“12÷3”）

师：这里的12表示什么？它是总数。3表示什么？是每份数。可以分给几只猴子就是求——？

生：份数。

2.探究12÷3的计算方法。

师：12÷3=？真的等于4吗？用你想到的方法说明12÷3=4。拿出《学习单》，完成第一题。

师：做好的同学跟同桌交流一下，你的方法是什么？

展示学生作品——

画图法：

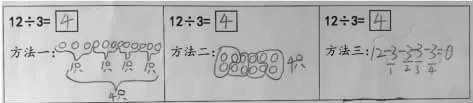
减法：

加法：

师：画图的方法听懂了吗？

生：每只小猴分3个，1个3就可以分给1只小猴，2个3可以分给2只小猴，3个3可以分给3只小猴，4个3分给4只小猴。

师：你的意思是，把桃子3个3个圈起来，能圈出几个3就可以分给几只小猴。4个3正好把12个桃子分完了，所以12÷3=4。是这样吗？

（板书：4个3）

师：通过画图的方法，我们知道12里面有几个3？12÷3等于几呀？

生：等于4。

师：（指减法 12-3-3-3-3=0）他用了什么方法？请你说说是怎么想的？

生：12减了1个3分给1只猴子，减2个3给2只猴子，减了4个3分给4只猴子。

师：这个3减给？这个3减给？……和前面画图的办法比一比，你想说什么？

生：前面是画出来看到12里面有4个3，现在他从12里面减了4次3，发现12里面有4个3。

师：（指减法）12减去4个3等于0说明——12里面有4个3。所以 12÷3=4。

师：（指加法 3+3+3+3=12）这个同学在想什么？

生：老师我想说一下，这个和减法也差不多。就是4个3加起来等于 12，所以 12÷3=4。

生：我想把乘法算式连到这里来。每只猴子分3个桃子，几个猴子就是几个3凑起来是12呢？我们就可以写算式3×（ ）=12。3×4=12，所以 12÷3=4。

生：要算12÷3等于几，就是要知道12里面有几个3。他们画图、减法、加法都是为了知道12里面有几个3。

3.探究4种方法之间的联系。

师：这4个方法之间有什么联系？

生：就是画图、加法、减法、乘法都是为了要知道12里面究竟有几个3。

生：虽然他们用的方法不同，但都是要知道12里面有几个3，几个3合起来是12。

师：你们最喜欢其中的哪个方法？

师：要求 12÷3，就是要知道12里面有几个3，要解决这个问题，可以倒过来想——几个3合起来是12，用哪个方法最容易知道几个3合起来是12？加法？减法？……

生：用乘法，3乘几等于12？三四十二！

师：老师和你们一样，比较这里的几种方法，它们的意思是一样的，而算起来是乘法最快。那我们就用乘法来求除法吧！

【反思：这次试教结束后，笔者问学生：“用乘法口诀求商，你们学会了吗？”学生回答：“学会了。”又追问：“是今天学会的，还是之前就会了？”学生诚实地回答：“之前就会了”。笔者调侃地问：“那这节课不是白上了吗？你们就这样傻傻地陪老师“演”了一节课？”学生们开心地笑了，有的忙摇手，着急地解释说：“不是，不是！孙老师，以前爷爷只告诉我除法可以用乘法口诀计算，今天我上过你的课以后，我知道了为什么可以用，其实乘法是和别的方法比较出来最方便的，大家才用乘法算除法的。”还有的学生说：“我们学减法的时候，有用加法来算减法的，后来学乘法，也有用加法算乘法的，今天学除法又知道了加法、减法、乘法都可以用来算除法，原来这些算法都是有关系的。”……

笔者被学生包围着，听着他们说出种种意想不到的精彩理解，感到了一种“专业”的自豪和幸福……】

四、教学启示

这一课多磨渐渐磨出了味道，仔细想来，教学用的例题没有变，平行班的学生，认知水平应该相差无几，那变化是怎么发生的？我想，主要在于本人对于“算法”和“算法多样化”的理解在深入。具体地说：

1.找准学生学习的需求点。

第一次试教，教师早早地借优生之口“告诉”大家计算除法可以使用口诀，然后大肆操练，自以为课堂效率高，殊不知学生“早就会了”。这是起点判断过低，课内重复课外已经习得的知识。

纵观平时的课堂，教师可能不舍得花时间前测或谈话，急匆匆拉开讲解的序幕，关注技能、技巧的落实，而忽视了让学生感受、理解数学知识产生和发展的过程。殊不知当今社会，资讯发达，越是技能、技巧，越有可能早早地被学生知道，但这种知道仅仅是知识的记忆、了解，好的教学应该直面这样的问题，激发学生进一步深入理解、探究的需要，从算法迈向算理、从机械模仿跃为自由创造。

2.把握所教内容的关键点。

教学设计要大气，可以抛出一个问题或一个任务让学生自主探究。而当学生自发生成了一些思路、方案的时候，教师要带领学生梳理、分类、比较、沟通和概括，实现知识的升华和内化。

本设计第二个版本，从学生自发的多样化开始，以自发的多样化告终，没有增量。没有增量，学生就会认为学习没有意义。

而在第三个版本中，有选择地呈现典型的方法，并通过反馈讲评积极促进学生对各种方法进行比较，发现其中的联系，画图、加法、减法、乘法看起来各不相同，其实质都在表征12里面有几个3，即几个3合起来是12。既然意义一样，乘法就从各种方法中脱颖而出，用乘法口诀求商成为学生的最优选择。这个过程使学生在个体认知背景下层层深入，建构除法计算知识，变被动操练为自觉学习，从而使学生感到课堂有了“味道”。

总之，数学教学要尊重学生的主体地位和主体人格，要适应学生思维发展的水平，提供学生认知发展的可能。对于计算教学，应该鼓励算法多样化，同时注意通性、通法的概括，注意寻求简洁合理的方法。促进学生理解的广度、深度和灵活度。